Tema 1 Muestreo estadístico

  • En todo estudio estadístico distinguiremos entre población, (conjunto de sujetos con una o varias características que podemos medir y deseamos estudiar), y muestra, (subconjunto de una población.)

  • Dos tipos de análisis estadístico:

    • Exploratorio o descriptivo: estadística descriptiva.
    • Inferencial o confirmatorio: estadística inferencial.

Pasos en un estudio inferencial:

  • Establecer la característica que se desea estimar o la hipótesis que se desea contrastar.

  • Determinar la información (los datos) que se necesita para hacerlo.

  • Diseñar un experimento que permita recoger estos datos; este paso incluye:

    • Decidir qué tipo de muestra se va a tomar y su tamaño.

    • Elegir las técnicas adecuadas para realizar las inferencias deseadas a partir de la muestra que se tomará.

  • Tomar una muestra y medir los datos deseados sobre los individuos que la forman.

  • Aplicar las técnicas de inferencia elegidas con el software adecuado.

  • Obtener conclusiones.

  • Si las conclusiones son fiables y suficientes, redactar un informe; en caso contrario, volver a empezar.

1.1 Tipos de muestreo

1.1.1 Muestreo aleatorio con reposición

Muestreo aleatorio: consiste en seleccionar una muestra de la población de manera que todas las muestras del mismo tamaño sean equiprobables.

Consideremos una urna de 100 bolas numeradas del 1 al 100:

Una urna de 100 bolas

Figure 1.1: Una urna de 100 bolas

Queremos extraer una muestra de 15 bolas. Para ello, podríamos repetir 15 veces el proceso de sacar una bola de la urna, anotar su número y devolverla a la urna. El tipo de muestra obtenida de esta manera recibe el nombre de muestra aleatoria con reposición, o simple (una m.a.s., para abreviar).

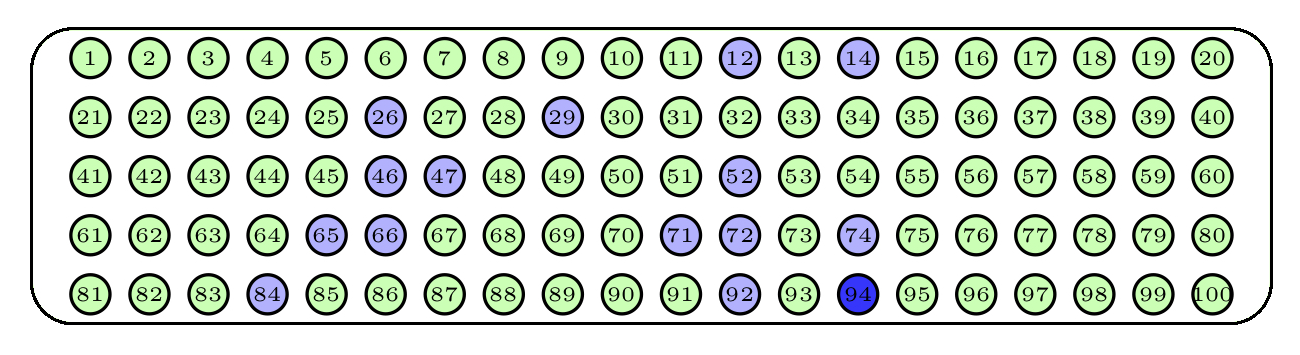
Una muestra aleatoria simple

Figure 1.2: Una muestra aleatoria simple

Las bolas violetas son las escogidas para la muestra. La bola azul se ha escogido dos veces al ser el muestreo con reposición.

Para simular un muestreo de 15 bolas con reposición en una urna de 100 en R, haríamos los siguiente:

sample(1:100, 15, replace=TRUE)
##  [1] 25  7 91 12  7 65 61 70 83 26 23 69 40 39 43

Fijaos que no hemos obtenido la misma muestra. Esto es debido a que no hemos fijado la semilla de aleatoriedad.

Ejemplo iris

Veamos un ejemplo más elaborado. Consideremos la tabla de datos iris que contiene 150 flores de 3 especies diferentes: setosa, versicolor y virginica. La tabla de datos contiene 5 variables: la longitud y amplitud del pétalo, la longitud y la amplitud del sépalo y la especie de la flor.

Las primeras filas de la tabla de datos son:

head(iris)
##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

Si quisiéramos una muestra de 10 flores con reposición, haríamos lo siguiente:

La función set.seed fija la semilla de aleatoriedad sirve para que siempre dé la misma muestra. A continuación, elegimos las flores de la muestra:

set.seed(4) 
flores.elegidas.10.con=sample(1:150,10,replace=TRUE)

Seguidamente, calculamos la subtabla de las flores de la muestra

muestra.iris.10.con = iris[flores.elegidas.10.con,]

Por último, mostramos la muestra de las flores:

muestra.iris.10.con 
##      Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
## 75            6.4         2.9          4.3         1.3 versicolor
## 51            7.0         3.2          4.7         1.4 versicolor
## 3             4.7         3.2          1.3         0.2     setosa
## 71            5.9         3.2          4.8         1.8 versicolor
## 115           5.8         2.8          5.1         2.4  virginica
## 51.1          7.0         3.2          4.7         1.4 versicolor
## 56            5.7         2.8          4.5         1.3 versicolor
## 62            5.9         3.0          4.2         1.5 versicolor
## 102           5.8         2.7          5.1         1.9  virginica
## 130           7.2         3.0          5.8         1.6  virginica

1.1.2 Muestreo aleatorio sin reposición

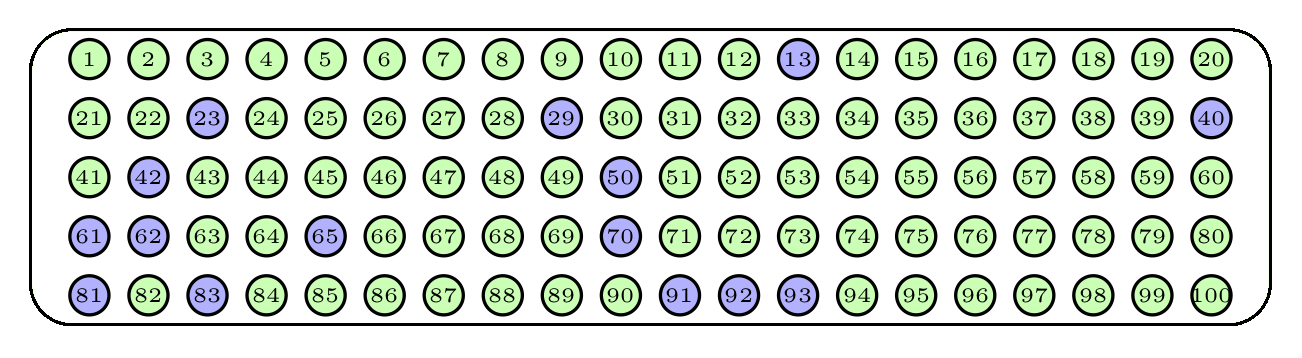
Muestra aleatoria sin reposición: Otra manera de extraer nuestra muestra sería repetir 15 veces el proceso de sacar una bola de la urna pero ahora sin devolverla. En este caso se habla de una muestra aleatoria sin reposición.

Una muestra aleatoria sin reposición

Figure 1.3: Una muestra aleatoria sin reposición

Para simular un muestreo de 15 bolas sin reposición en la urna anterior de 100 en R, haríamos los siguiente:

sample(1:100, 15, replace=FALSE)
##  [1] 24  1 84 35 27 48 95  2 32 47 44 69 15 22 89

Ejemplo iris

Consideremos de nuevo la tabla de datos iris.

Para obtener una muestra de 10 flores sin reposición, haríamos los pasos siguientes:

Primero elegimos las flores de la muestra

set.seed(4) 
flores.elegidas.10.sin=sample(1:150,10,replace=FALSE)

A continuación, calculamos la subtabla de las flores de la muestra

muestra.iris.10.sin = iris[flores.elegidas.10.sin,]

Por último, mostramos las muestra de las flores:

muestra.iris.10.sin 
##     Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
## 75           6.4         2.9          4.3         1.3 versicolor
## 51           7.0         3.2          4.7         1.4 versicolor
## 3            4.7         3.2          1.3         0.2     setosa
## 71           5.9         3.2          4.8         1.8 versicolor
## 115          5.8         2.8          5.1         2.4  virginica
## 149          6.2         3.4          5.4         2.3  virginica
## 56           5.7         2.8          4.5         1.3 versicolor
## 62           5.9         3.0          4.2         1.5 versicolor
## 102          5.8         2.7          5.1         1.9  virginica
## 130          7.2         3.0          5.8         1.6  virginica

1.1.3 Muestras aleatorias con reposición vs. sin reposición

Observación: ¿Cuándo se puede considerar equivalente válido realizar una muestra con reposición que sin reposición?

Si el tamaño de la población es muy grande en relación al de la muestra (por dar una regla, digamos que, al menos, unas 1000 veces mayor).

1.1.4 Muestreo sistemático

Muestreo sistemático: Supongamos que los individuos de una población vienen dados en forma de una lista ordenada. El muestreo sistemático consiste en tomarlos a intervalos constantes escogiendo al azar el primer individuo que elegimos.

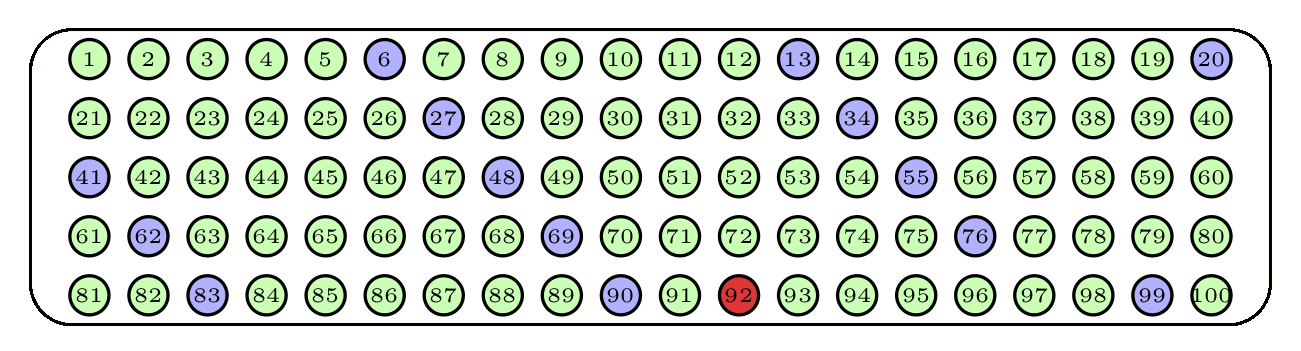
Una muestra aleatoria sistemática

Figure 1.4: Una muestra aleatoria sistemática

La figura anterior describe una muestra aleatoria sistemática de 15 bolas de nuestra urna de 100 bolas: hemos empezado a escoger por la bola roja oscura, que ha sido elegida al azar, y a partir de ella hemos tomado 1 de cada 7 bolas, volviendo al principio cuando hemos llegado al final de la lista de bolas.

Ejemplo iris

Vamos a calcular una muestra aleatoria sistemática de la tabla de datos iris de tamaño 10.

Primero fijamos la semilla de aleatoriedad para la reproducibilidad del experimento:

set.seed(15)

Seguidamente, hallamos la etiqueta de la primera flor de la muestra (que será una de las 150 de la tabla de datos):

(primera.flor=sample(1:150,1)) 
## [1] 37

A continuación, hallamos el incremento que vamos a ir sumando a la primera etiqueta que hemos elegido:

incremento = floor(150/10)

el siguiente paso es elegir las flores de la muestra

flores.elegidas.10.sis = seq(from=primera.flor,by=incremento,length.out=10)

como las etiquetas elegidas no están entre 1 y 150, hemos de transformarlas:

flores.elegidas.10.sis = flores.elegidas.10.sis%%150

a continuación, calculamos la subtabla de las flores de la muestra

muestra.iris.10.sis = iris[flores.elegidas.10.sis,]

Y finalmente mostramos la subtabla de la muestra

muestra.iris.10.sis 
##     Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
## 37           5.5         3.5          1.3         0.2     setosa
## 52           6.4         3.2          4.5         1.5 versicolor
## 67           5.6         3.0          4.5         1.5 versicolor
## 82           5.5         2.4          3.7         1.0 versicolor
## 97           5.7         2.9          4.2         1.3 versicolor
## 112          6.4         2.7          5.3         1.9  virginica
## 127          6.2         2.8          4.8         1.8  virginica
## 142          6.9         3.1          5.1         2.3  virginica
## 7            4.6         3.4          1.4         0.3     setosa
## 22           5.1         3.7          1.5         0.4     setosa

1.1.5 Muestreo aleatorio estratificado

Muestreo aleatorio estratificado: Este tipo de muestreo se utiliza cuando la población está clasificada en estratos que son de interés para la propiedad estudiada. Se toma una muestra aleatoria de cada estrato y se unen en una muestra global. A este proceso se le llama muestreo aleatorio estratificado.

Supongamos que nuestra urna de 100 bolas contiene 40 bolas de un color y 60 de otro color tal como muestra la figura:

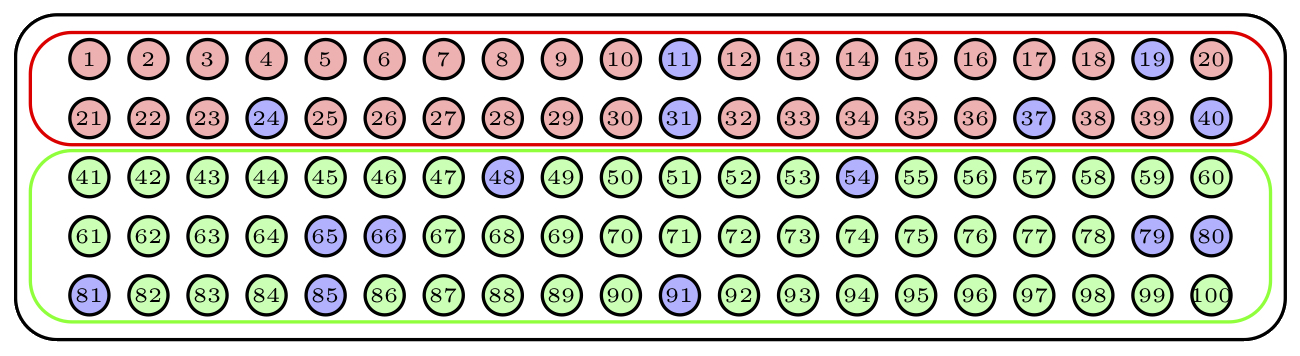
Una muestra aleatoria estratificada con dos estratos

Figure 1.5: Una muestra aleatoria estratificada con dos estratos

Para tomar una muestra aleatoria estratificada de 15 bolas, considerando como estratos los dos colores, tomaríamos una muestra aleatoria de 6 bolas del primer color y una muestra aleatoria de 9 bolas del segundo color.

Ejemplo iris

Vamos a considerar que la tabla de datos iris está estratificada según tres estratos. Cada estrato está compuesto por las 50 flores de la misma especie. Vamos a hallar una muestra de tamaño 12 hallando tres muestras de tamaño 4 de cada especie (estrato) con reposición y después juntaremos la tres submuestras.

En primer lugar, fijamos la semilla de aleatoriedad por reproducibilidad:

set.seed(25)

a continuación, hallamos las flores de la muestra de cada una de las especies:

fls.muestra.setosa=sample(1:50,4,replace=TRUE) 
fls.muestra.versicolor=sample(51:100,4,replace=TRUE) 
fls.muestra.virginica=sample(101:150,4,replace=TRUE)

seguidamente, calculamos y mostramos la muestra estratificada juntando las tres muestras de cada especie

(muestra.iris.est=rbind(iris[fls.muestra.setosa,],iris[fls.muestra.versicolor,],
                       iris[fls.muestra.virginica,]))
##     Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
## 7            4.6         3.4          1.4         0.3     setosa
## 29           5.2         3.4          1.4         0.2     setosa
## 24           5.1         3.3          1.7         0.5     setosa
## 25           4.8         3.4          1.9         0.2     setosa
## 99           5.1         2.5          3.0         1.1 versicolor
## 58           4.9         2.4          3.3         1.0 versicolor
## 91           5.5         2.6          4.4         1.2 versicolor
## 76           6.6         3.0          4.4         1.4 versicolor
## 116          6.4         3.2          5.3         2.3  virginica
## 136          7.7         3.0          6.1         2.3  virginica
## 101          6.3         3.3          6.0         2.5  virginica
## 108          7.3         2.9          6.3         1.8  virginica

1.1.6 Muestreo por conglomerados

El proceso de obtener y estudiar una muestra aleatoria en algunos casos es caro o difícil, incluso aunque dispongamos de la lista completa de la población.

Muestreo por conglomerados: una alternativa posible sería, en vez de extraer una muestra aleatoria de todos los individuos de la población, escoger primero al azar unos subconjuntos en los que la población está dividida, a las que llamamos en este contexto conglomerados (clusters).

Supongamos que las 100 bolas de nuestra urna se agrupan en 20 conglomerados de 5 bolas cada uno según las franjas verticales.

Para obtener una muestra aleatoria por conglomerados de tamaño 15, escogeríamos al azar 3 conglomerados y la muestra estaría formada por sus bolas: los conglomerados escogidos están marcados en azul:

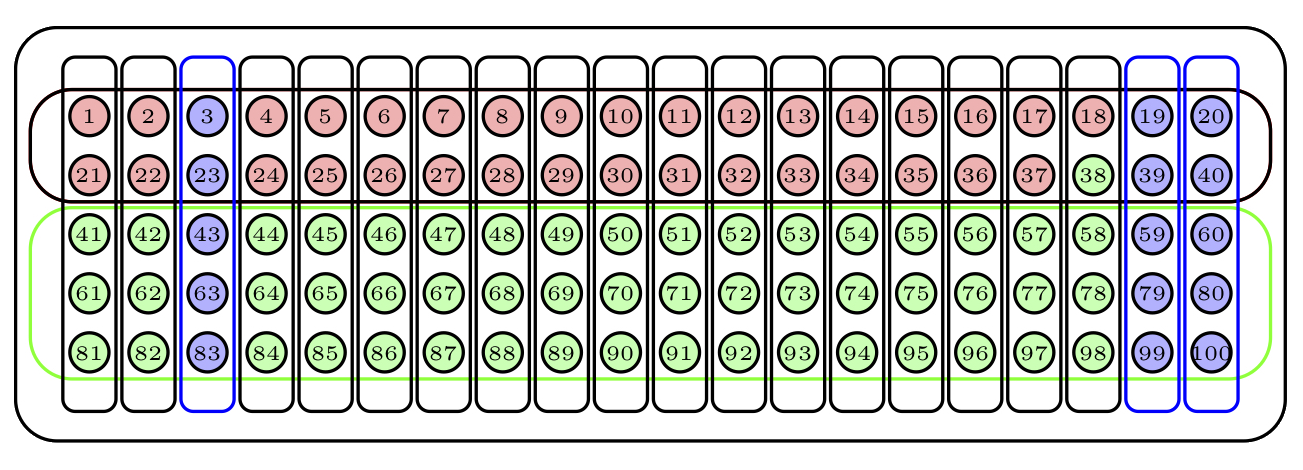
Una muestra aleatoria por conglomerados con 2 estratos y 20 conglomerados

Figure 1.6: Una muestra aleatoria por conglomerados con 2 estratos y 20 conglomerados

Ejemplo worldcup

Consideremos la tabla de datos worldcup del paquete faraway. Esta tabla de datos nos da información sobre 595 jugadores que participaron en el Mundial de Futbol del año 2010 celebrado en Sudáfrica. La tabla nos da la información siguiente sobre cada jugador:

  • Team: país del jugador.
  • Position: posición en la juega el jugador: Defender (defensa), Forward (delantero), GoalKeeper (portero) y Midfielder (centrocampista)
  • Time: tiempo que ha jugado el jugador en minutos.
  • Shots: número de tiros a puerta.
  • Passes: número de pases.
  • Tackles: número de entradas.
  • Saves: número de paradas.
library(faraway)
head(worldcup)
##                Team   Position Time Shots Passes Tackles Saves
## Abdoun      Algeria Midfielder   16     0      6       0     0
## Abe           Japan Midfielder  351     0    101      14     0
## Abidal       France   Defender  180     0     91       6     0
## Abou Diaby   France Midfielder  270     1    111       5     0
## Aboubakar  Cameroon    Forward   46     2     16       0     0
## Abreu       Uruguay    Forward   72     0     15       0     0

Ejemplo

Supongamos que queremos calcular una muestra de tamaño indeterminado de los jugadores por conglomerados eligiendo como conglomerados los países a los que éstos pertenecen.

En la tabla de datos hay un total de 32 países.

Elegiremos primero 4 países aleatoriamente y la muestra elegida serán los jugadores que pertenecen a dichos países:

set.seed(19)
números.países.elegidos = sample(1:32,4,replace=FALSE) 
países.elegidos = unique(worldcup$Team)[números.países.elegidos]

Los países elegidos son:

países.elegidos
## [1] Slovakia    Mexico      New Zealand France     
## 32 Levels: Algeria Argentina Australia Brazil Cameroon Chile ... Uruguay

La muestra elegida estará formada por los jugadores que perteneces a dichos países:

muestra.worldcup.con = worldcup[worldcup$Team%in%países.elegidos,]

Dicha muestra tiene tamaño 73. Sólo mostramos los datos de los 8 primeros jugadores:

head(muestra.worldcup.con,8)
##                    Team   Position Time Shots Passes Tackles Saves
## Abidal           France   Defender  180     0     91       6     0
## Abou Diaby       France Midfielder  270     1    111       5     0
## Aguilar          Mexico   Defender   55     0     31       2     0
## Alou Diarra      France Midfielder   82     0     31       0     0
## Anelka           France    Forward  117     7     37       1     0
## Barrera          Mexico Midfielder  149     4     59       2     0
## Barron      New Zealand Midfielder    1     0      0       0     0
## Bautista         Mexico    Forward   45     0      8       3     0

1.1.7 Muestreo polietápico

Muestreo polietápico: si una vez seleccionada la muestra aleatoria de conglomerados, tomamos de alguna manera una muestra aleatoria de cada uno de ellos, estaremos realizando un muestreo polietápico.

La figura muestra un ejemplo sencillo de muestreo polietápico de nuestra urna: hemos elegido al azar 5 conglomerados (marcados en azul) y de cada uno de ellos hemos elegido 3 bolas al azar sin reposición.

Una muestra polietápica de 5 conglomerados y 3 bolas al azar sin reposición

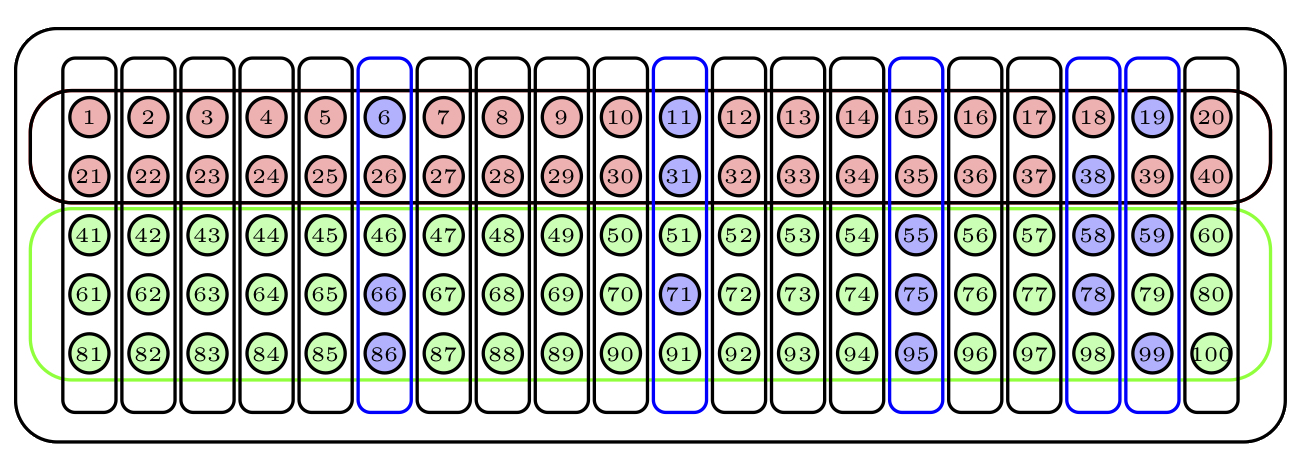
Figure 1.7: Una muestra polietápica de 5 conglomerados y 3 bolas al azar sin reposición

Ejemplo worldcup

Para realizar un muestreo polietápico con los datos del ejemplo anterior (tabla de datos worldcup), podemos elegir una submuestra de 5 jugadores para cada uno de los 4 países elegidos, obteniendo al final una muestra de tamaño 20 de todos los jugadores de la tabla de datos.

Primero definimos las 4 subtablas de datos para los jugadores de cada país elegido:

worldcup.pais1 = worldcup[worldcup$Team==países.elegidos[1],]
worldcup.pais2 = worldcup[worldcup$Team==países.elegidos[2],]
worldcup.pais3 = worldcup[worldcup$Team==países.elegidos[3],]
worldcup.pais4 = worldcup[worldcup$Team==países.elegidos[4],]

A continuación elegimos los 5 jugadores de cada país:

set.seed(28) 
jugadores.pais1 = sample(1:dim(worldcup.pais1)[1],5,replace=FALSE)
jugadores.pais2 = sample(1:dim(worldcup.pais2)[1],5,replace=FALSE)
jugadores.pais3 = sample(1:dim(worldcup.pais3)[1],5,replace=FALSE)
jugadores.pais4 = sample(1:dim(worldcup.pais4)[1],5,replace=FALSE)

Por último juntamos las submuestras obtenidas de los jugadores de cada país:

muestra.worldcup.pol = rbind(worldcup.pais1[jugadores.pais1,],
                             worldcup.pais2[jugadores.pais2,],
                             worldcup.pais3[jugadores.pais3,],
                             worldcup.pais4[jugadores.pais4,])

Y finalmente los mostramos por pantalla: (mostramos sólo los 12 primeros)

head(muestra.worldcup.pol,12)
##                  Team   Position Time Shots Passes Tackles Saves
## Stoch        Slovakia Midfielder  193     2     76       1     0
## Zabavnik     Slovakia   Defender  268     1     94       8     0
## Kucka        Slovakia Midfielder  181     4     71      10     0
## Weiss        Slovakia Midfielder  269     2     84       2     0
## Durica       Slovakia   Defender  360     1    159       4     0
## PerezM         Mexico Goalkeeper  360     0     58       0    13
## Moreno         Mexico   Defender  147     0     74       4     0
## Aguilar        Mexico   Defender   55     0     31       2     0
## Bautista       Mexico    Forward   45     0      8       3     0
## Hernandez      Mexico    Forward  169     6     37       1     0
## Nelsen    New Zealand   Defender  270     0     92       1     0
## Reid      New Zealand   Defender  270     2     90      10     0

1.2 Guía rápida en R

  • sample(x, n, replace=...) genera una muestra aleatoria de tamaño n del vector x. Si x es un número natural x, representa el vector \(1,2,\ldots,x\). Dispone de los dos parámetros siguientes:

    • replace que igualado a TRUE produce muestras con reposición e igualado a FALSE (su valor por defecto) produce muestras sin reposición.
    • prob, que permite especificar las probabilidades de aparición de los diferentes elementos de x (por defecto, son todas la misma).

  • set.seed permite fijar la semilla de aleatoriedad.