Tema 2 Estimación Puntual
El problema usual de la estadística inferencial es:
Queremos conocer el valor de una característica en una población
No podemos medir esta característica en todos los individuos de la población
Extraemos una muestra aleatoria de la población, medimos la característica en los individuos de esta muestra e inferimos el valor de la característica para la toda la población
- ¿Cómo lo tenemos que hacer?
- ¿Cómo tenemos que hacer la muestra?
- ¿Qué información podemos inferir?
Ejemplo
Escogemos al azar \(n\) estudiantes de la Universidad de las Islas Baleares (UIB) (con reposición) para medirles la estatura
De esta manera, todas las muestras posibles de \(n\) individuos (posiblemente repetidos: multiconjuntos) tienen la misma probabilidad
Ejemplo
La media de las estaturas de una muestra de estudiantes de la UIB nos permite estimar la media de las alturas de todos los estudiantes de la UIB.
un conjunto de \(n\) copias independientes de \(X\), o
un conjunto de \(n\) variables aleatorias independientes \(X_1,\ldots,X_n\), todas con la distribución de \(X\).
Ejemplo
Sea \(X\) la v.a. “escogemos un estudiante de la UIB y le medimos la altura”. Una m.a.s. de \(X\) de tamaño \(n\) serán \(n\) copias independientes \(X_1,\ldots,X_n\) de esta \(X\).
Ejemplo:
La media muestral de las alturas de una realización de una m.a.s. de las alturas de estudiantes estima la altura media de un estudiante de la UIB.
Así pues, un estadístico es una (otra) variable aleatoria, con distribución, esperanza, etc.
La distribución muestral de \(T\) es la distribución de esta variable aleatoria.
Estudiando esta distribución muestral, podremos estimar propiedades de \(X\) a partir del comportamiento de una muestra.
Convenio: LOS ESTADÍSTICOS, EN MAYÚSCULAS; las realizaciones, en minúsculas
\(X_1,\ldots,X_n\) una m.a.s. y \[ \overline{X}:=\frac{X_1+\cdots+X_n}{n}, \] el estadístico media muestral.
\(x_1,\ldots,x_n\) una realización de esta m.a.s. y \[ \overline{x}:=\frac{x_1+\cdots+x_n}{n}, \] la media (muestral) de esta realización.
En la vida real, las muestras aleatorias se toman, casi siempre, sin reposición (es decir sin repetición del mismo individuo de la población).
No son muestras aleatorias simples. pero:
Si \(N\) es mucho más grande que \(n\), los resultados para una m.a.s. son (aproximadamente) los mismos, ya que las repeticiones son improbables y las variables aleatorias que forman la muestra son prácticamente independientes.
En estos casos cometeremos el abuso de lenguaje de decir que es una m.a.s.
Si \(n\) es relativamente grande, se suelen dar versiones corregidas de los estadísticos.
2.1 La media muestral
2.1.1 Definición de media muestral
La media muestral es: \[ \overline{X}=\frac{X_1+\cdots+X_n}{n} \]
En estas condiciones, \[ E(\overline{X})=\mu_X,\quad \sigma_{\overline{X}}=\frac{\sigma_X}{\sqrt{n}} \] donde \(\sigma_{\overline{X}}\) es el error estándar de \(\overline{X}\).
2.1.2 Propiedades de la media muestral
Es un estimador puntual de \(\mu_X\)
\(E(\overline{X})=\mu_X\): el valor esperado de \(\overline{X}\) es \(\mu_X\).
Si tomamos muchas veces una m.a.s. y calculamos la media muestral, el valor medio de estas medias tiende con mucha probabilidad a ser \(\mu_X\).
\(\sigma_{\overline{X}}= \sigma_X/\sqrt{n}\): la variabilidad de los resultados de \(\overline{X}\) tiende a 0 a medida que tomamos muestras más grandes.
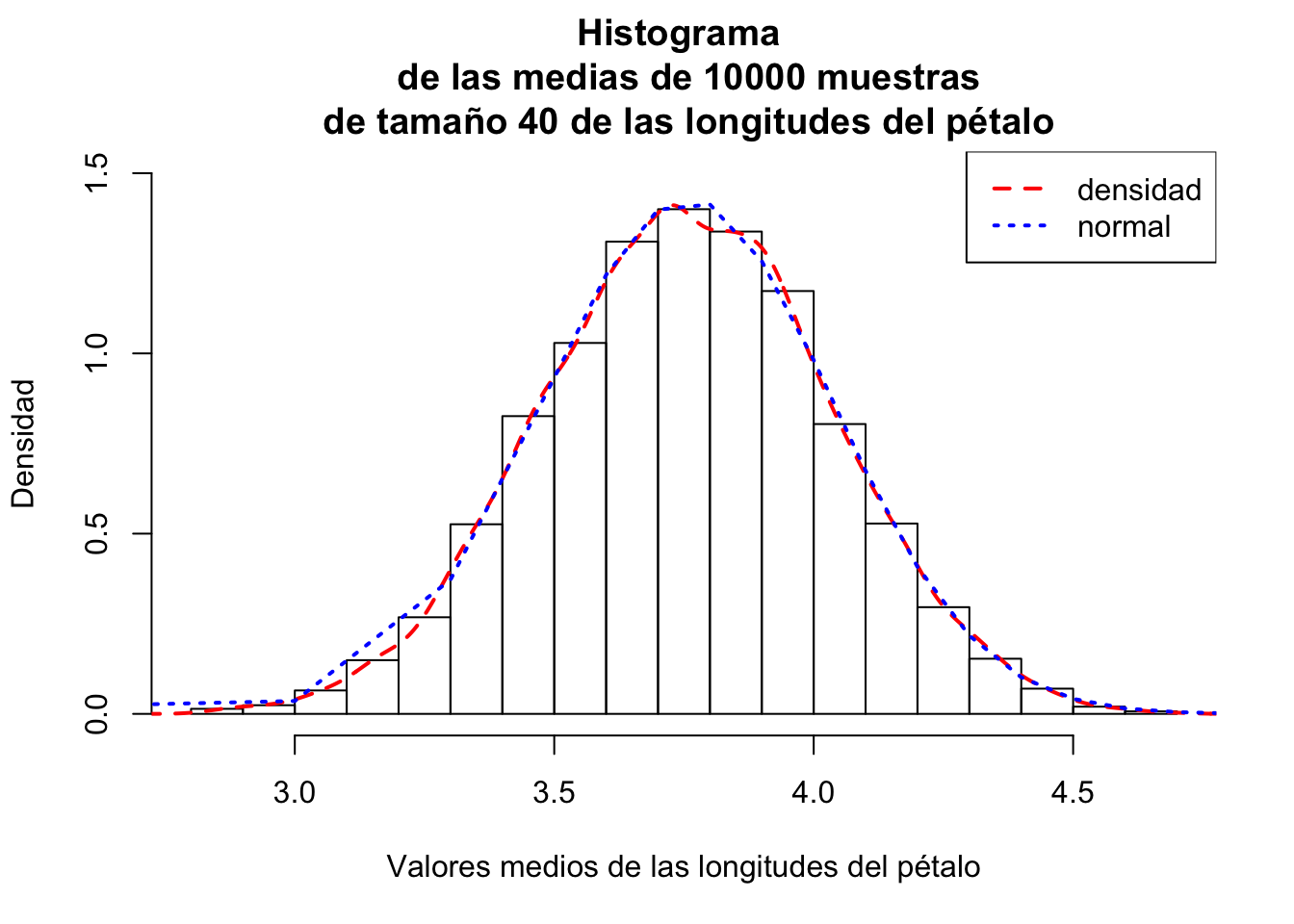
Ejemplo del iris
Consideremos la tabla de datos iris (que ya vimos en el tema de Muestreo).
Vamos a comprobar las propiedades anteriores sobre la variable longitud del pétalo (Petal.Length).
- Generaremos 10000 muestras de tamaño 40 con reposición de las longitudes del pétalo.
- A continuación hallaremos los valores medios de cada muestra.
- Consideraremos la media y la desviación típica de dichos valores medios y los compararemos con los valores exactos dados por las propiedades de la media muestral.
Para generar los valores medios de las longitudes del pétalo de las 10000 muestras usaremos la función replicate de R. Fijaos en su sintaxis:
replicate(n,expresión)evalúanveces laexpresión, y organiza los resultados como las columnas de una matriz (o un vector, si el resultado de cadaexpresiónes unidimensional).
set.seed(1001)
valores.medios.long.pétalo=replicate(10000,mean(sample(iris$Petal.Length,40,
replace =TRUE)))Los valores medios de las 10 primeras muestras anteriores serían
## [1] 3.5975 3.5150 3.9400 3.2650 3.9125 3.9650 4.2825 3.2950 3.8500 3.7850El valor medio de los valores medios de las muestras anteriores vale:
## [1] 3.754478Dicho valor tiene que estar cerca del valor medio de la variable longitud del pétalo:
## [1] 3.758Fijaos que los dos valores están muy próximos.
La desviación típica de los valores medios de las muestras vale:
## [1] 0.27965126Dicho valor tiene que estar cerca de \(\frac{\sigma_{lp}}{\sqrt{40}}\) (donde \(\sigma_{lp}\) es la desviación típica de la variable longitud del pétalo) tal como predice la propiedad de la media muestral referida a la desviación típica de la misma:
## [1] 0.27911816Fijaos también en que los dos valores están muy próximos.
2.2 Poblaciones normales
2.2.1 Combinación lineal de distribuciones normales
\(E(Y)=a_1\cdot\mu_1+\cdots+a_n\cdot\mu_n+b\)
\(\sigma(Y)^2=a_1^2\cdot\sigma_1^2+\cdots+a_n^2\cdot\sigma_n^2\)
2.2.2 Distribución de la media muestral
Veamos cómo se distribuye la media muestral en el caso en que la población \(X\) sea normal.
Sea \(X_1,\ldots, X_n\) una m.a.s. de una v.a. \(X\) de esperanza \(\mu_X\) y desviación típica \(\sigma_X\).
Si \(X\) es \(N(\mu_X,\sigma_X)\), entonces \[ \overline{X}\mbox{ es }N\Big(\mu_X,\frac{\sigma_X}{\sqrt{n}}\Big) \] y por lo tanto \[ Z=\frac{\overline{X}-\mu_X}{\frac{\sigma_X}{\sqrt{n}}}\mbox{ es }N(0,1) \]
\(Z\) es la expresión tipificada de la media muestral.
2.2.3 Teorema Central del Límite
Ejemplo
Tenemos una v.a. \(X\) de media \(\mu_X=3\) y desviación típica. \(\sigma_X=0.2\). Tomamos muestras aleatorias simples de tamaño 50. La distribución de la media muestral \(\overline{X}\) es aproximadamente \[ N\left(3,\frac{0.2}{\sqrt{50}}\right)=N(3,0.0283). \]
En el gráfico siguiente podemos observar el histograma de los valores medios de las longitudes del pétalo de las 10000 muestras junto con la distribución normal correspondiente:
Ejercicio
El tamaño en megabytes (MB) de un tipo de imágenes comprimidas tiene un valor medio de \(115\) MB, con una desviación típica de \(25\). Tomamos una m.a.s. de \(100\) imágenes de este tipo.
¿Cuál es la probabilidad de que la media muestral del tamaño de los ficheros sea \(\leq 110\) MB?
Sea \(X\) la variable aleatoria que nos da el tamaño en megabytes del tipo de imágenes comprimidas. La distribución de \(X\) será \(X=N(\mu=115,\sigma = 25)\)
Sea \(X_1,\ldots,X_{100}\) la m.a.s. La distribución aproximada de la media muestral \(\overline{X}\) usando el Teorema Central del Límite será: \(\overline{X}\approx N\left(\mu_{\overline{X}}=115,\sigma_{\overline{X}}=\frac{25}{\sqrt{100}}=2.5\right)\).
Nos piden la probabilidad siguiente: \(P(\overline{X}\leq 110)\). Si estandarizamos:
\[ P(\overline{X}\leq 110)=P\left(Z=\frac{\overline{X}-115}{2.5}\leq \frac{110-115}{2.5}\right) =p(Z\leq -2)=0.0228. \] donde \(Z\) es la normal estándar \(N(0,1)\)
2.2.4 Media muestral en muestras sin reposición
Sea \(X_1,\ldots, X_n\) una m.a. sin reposición de tamaño \(n\) de una v.a. \(X\) de esperanza \(\mu_X\) y desviación típica \(\sigma_X\).
Si \(n\) es pequeño en relación al tamaño \(N\) de la población, todo lo que hemos contado funciona (aproximadamente).
Si \(n\) es grande en relación a \(N\), entonces \[ E(\overline{X})=\mu_X,\quad \sigma_{\overline{X}}=\frac{\sigma_X}{\sqrt{n}}\cdot \sqrt{\frac{N-n}{N-1}} \] (factor de población finita)
El Teorema Central del Límite ya no funciona exactamente en este último caso.
2.3 Proporción muestral
2.3.1 Proporción muestral. Definición
\(S=\sum_{i=1}^n X_i\) es el nombre de éxitos observados es \(B(n,p)\).
La proporción muestral es \[ \widehat{p}_X=\frac{S}{n} \] y es un estimador de \(p_X\).
Notemos que \(\widehat{p}_X\) es un caso particular de \(\overline{X}\), por lo que todo lo que hemos dicho para medias muestrales es cierto para proporciones muestrales.
2.3.2 Proporción muestral. Propiedades
Valor esperado de la proporción muestral: \[E(\widehat{p}_X)=p_X\]
Error estándar de la proporción muestral:
\[\displaystyle \sigma_{\widehat{p}_X}=\sqrt{\frac{p_X(1-p_X)}{n}}\]
- Si la muestra es sin reposición y \(n\) es relativamente grande,
\[\displaystyle\sigma_{\widehat{p}_X}=\sqrt{\frac{p_X(1-p_X)}{n}}\cdot{\sqrt{\frac{N-n}{N-1}}}.\]
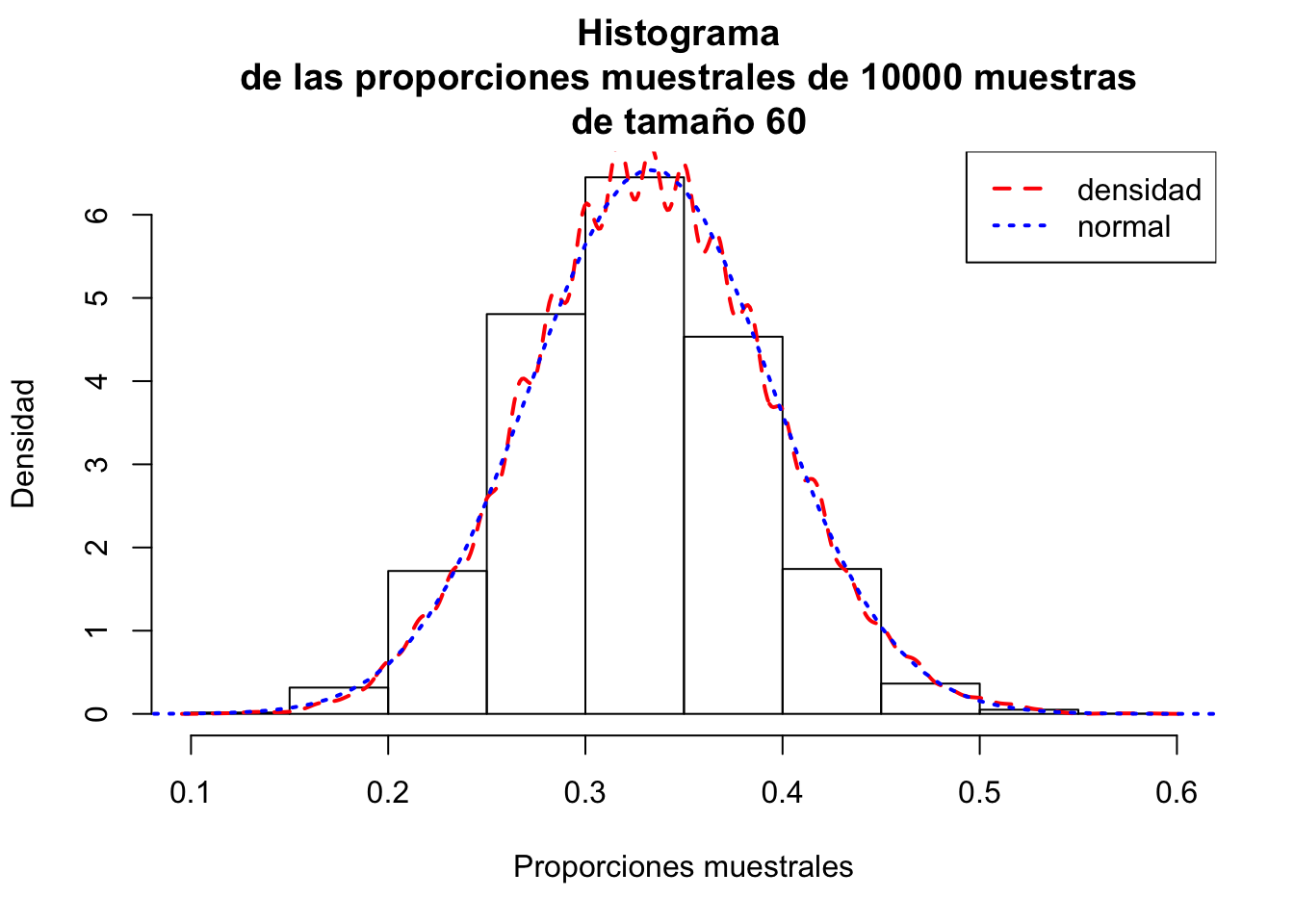
Ejemplo del iris
Dada una muestra de 60 flores de la tabla de datos iris,
- Estimar la proporción de flores de la especie
setosa. - Estimar también la desviación estándar de dicha proporción.
Primero generamos la muestra de las 60 flores:
set.seed(1000)
flores.elegidas = sample(1:150,60,replace=TRUE)
muestra.flores = iris[flores.elegidas,]A continuación miramos cuántas flores de la muestra son de la especie setosa:
##
## FALSE TRUE
## 39 21Tenemos entonces 21 flores de la especie setosa.
La estimación de la proporción de flores de especie setosa será:
## TRUE
## 0.35valor que no está muy lejos del valor poblacional de la proporción \(p_{setosa}\) que es \(p_{setosa}=\frac{50}{150}=0.3333\).
Para estimar la desviación estándar de la proporción muestral de flores de tamaño 60 de la especie setosa, repetiremos el experimento anterior 10000 veces y hallaremos la desviación estándar de las proporciones obtenidas. Al final, compararemos dicho valor con el valor exacto dado por la propiedad correspondiente.
Para generar las proporciones de las 10000 muestras usaremos la función replicate de R:
set.seed(1002)
props.muestrales = replicate(10000,table(sample(iris$Species,60,
replace=TRUE)=="setosa")[2]/60)La desviación típica de las proporciones muestrales anteriores vale:
## [1] 0.060210983valor muy próximo al valor real que vale: \(\displaystyle \sigma_{\widehat{p}_X}=\sqrt{\frac{p_X(1-p_X)}{n}}= \sqrt{\frac{\frac{50}{150}\cdot \left(1-\frac{50}{150}\right)}{60}}=0.0609\).
En el gráfico siguiente podemos observar el histograma de las proporciones muestrales de las 10000 muestras junto con la distribución normal correspondiente:
2.4 Varianza muestral y desviación típica muestral
La varianza muestral es \[ \widetilde{S}_{X}^2=\frac{\sum\limits_{i=1}^n (X_{i}-\overline{X})^2}{n-1} \] La desviación típica muestral es \[ \widetilde{S}_{X}=+\sqrt{\widetilde{S}_{X}^2} \]
Además, escribiremos \[ S^2_{X}=\frac{\sum\limits_{i=1}^n (X_{i}-\overline{X})^2}{n}=\frac{(n-1)}{n}\widetilde{S}^2_{X}\quad\mbox{ y }\quad S_X=+\sqrt{S_X^2} \]
\[\displaystyle \widetilde{S}_{X}^2=\frac{n}{n-1}\left(\frac{\sum\limits_{i=1}^n X_{i}^2}{n}-\overline{X}^2\right)\]
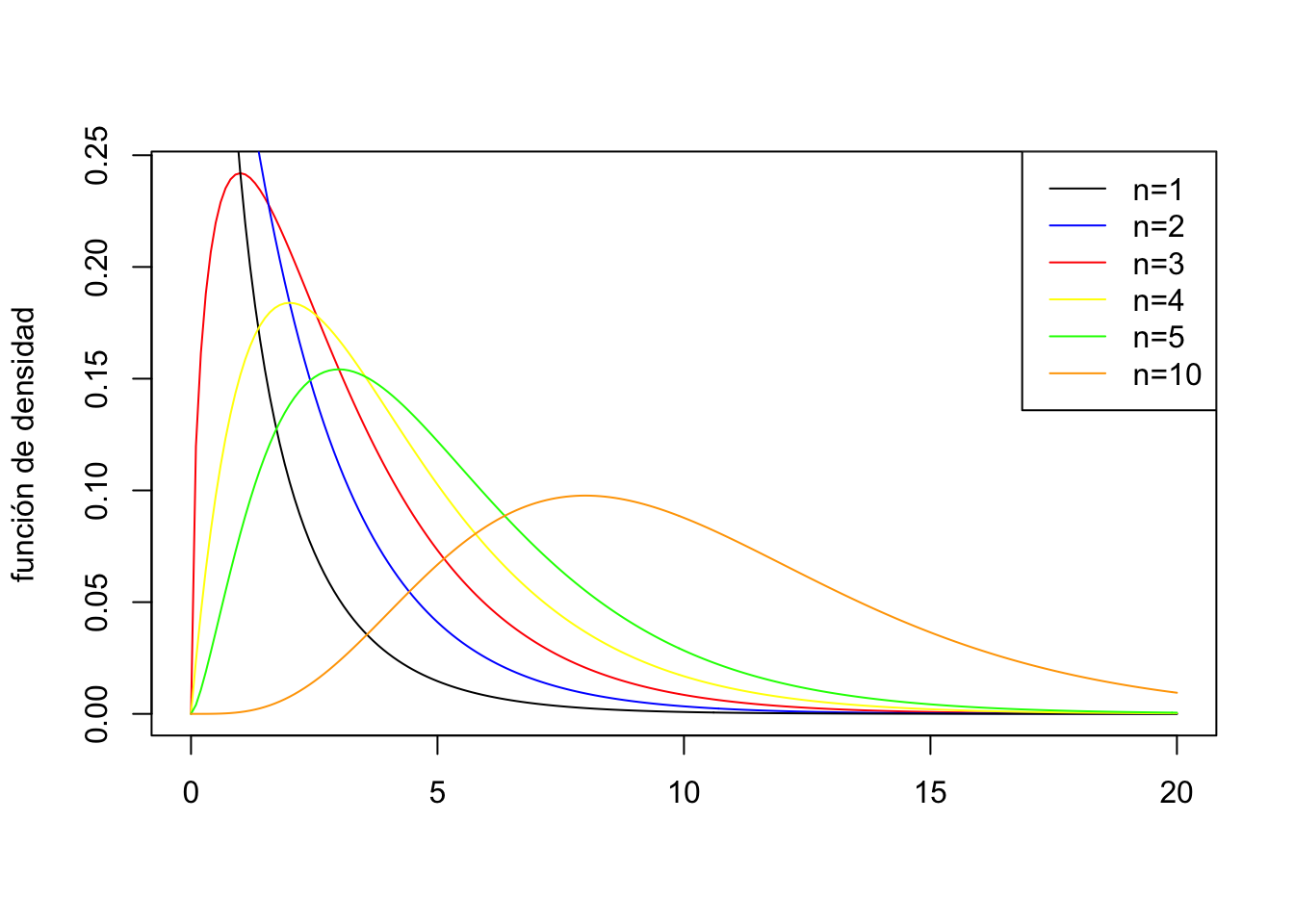
La distribución \(\chi_n^2\) (\(\chi\): en catalán, khi; en castellano, ji; en inglés, chi), donde \(n\) es un parámetro llamado grados de libertad:
es la de \[ X=Z_{1}^{2}+Z_{2}^{2}+\cdots +Z_{n}^{2} \] donde \(Z_{1},Z_{2},\ldots, Z_{n}\) son v.a. independientes \(N(0,1)\).
Su función de densidad es: \[ f_{\chi_n^2}(x)={\frac{1}{2^{n/2} \Gamma (n/2)}} x^{(n/2)-1} e^{-x/2},\quad\mbox{ si $x\geq 0$} \] donde \(\Gamma(x)=\int_{0}^{\infty} t^{x-1}e^{-t}\, dt\), si \(x> 0\).
Si \(X_{\chi_n^2}\) es una v.a. con distribución \(\chi_n^2\), \[E\left(X_{\chi_n^2}\right)=n,\quad Var\left(X_{\chi_n^2}\right)=2 n\]
\({\chi_n^2}\) se aproxima a una distribución normal \(N\left(n,\sqrt{2n}\right)\) para \(n\) grande (\(n>40\) o \(50\)).
Ejemplo
Supongamos que el aumento diario del la ocupación de una granja de discos duros medido en Gigas sigue una distribución normal con desviación típica \(1.7\). Se toma una muestras de 12 discos. Supongamos que esta muestra es pequeña respecto del total de la población de la granja de discos.
¿Cual es la probabilidad de que la desviación típica muestral sea \(\leq 2.5\)?
Sea \(X\)= aumento diario en Gigas de un disco duro elegido al azar.
Sabemos que \(\sigma_{X}^2=(1.7)^2=2.89.\)
Como que \(X\) es normal y \(n=12\), tenemos que \[ \frac{11\cdot \widetilde{S}_{X}^2}{2.89}=\frac{(n-1)\widetilde{S}_{X}^2}{\sigma_{X}^2}\sim \chi^2_{11} \]
Nos piden: \(\displaystyle P(\widetilde{S}_{X}<2.5)= P\left(\widetilde{S}_{X}^2<2.5^2\right)\): \[ P\left(\widetilde{S}_{X}^2<2.5^2\right) = P\left(\frac{11\cdot \widetilde{S}_{X}^2}{2.89}<\frac{11 \cdot 2.5^2}{2.89}\right) = P(\chi_{11}^2<23.7889) =0.9863. \]
2.5 Propiedades de los estimadores
2.5.1 Estimadores insesgados
¿Cuándo un estimador es bueno?
El sesgo de \(\widehat{\theta}\) es la diferencia \[E(\widehat{\theta})-\theta\]
\(\overline{X}\) es estimador no sesgado de \(\mu_X\): \(E(\overline{X})=\mu_X\).
\(\widehat{p}_X\) es estimador no sesgado de \(p_X\): \(E(\widehat{p}_X)=p_X\).
Si \(X\) es normal: \(\widetilde{S}_{X}^2\) es estimador no sesgado de \(\sigma_X^2\): \(E(\widetilde{S}_{X}^2)=\sigma_X^2\)
Si \(X\) es normal: \(E({S}_{X}^2)=\dfrac{n-1}{n}\sigma_X^2\). Por lo tanto \({S}_{X}^2\), es sesgado, con sesgo \[ E({S}_{X}^2)-\sigma_X^2=\dfrac{n-1}{n}\sigma_X^2-\sigma_X^2=-\dfrac{\sigma_X^2}{n}\mbox{ que tiende a }0. \]
2.5.2 Estimadores eficientes
¿Cuando un estimador es bueno?
Cuando es no segado y tiene poca variabilidad (así es más probable que aplicado a una m.a.s. dé un valor más cercano al valor esperado)
\[\sigma_{\widehat{\theta}_1}< \sigma_{\widehat{\theta}_2},\] es decir, cuando \[Var(\widehat{\theta}_1)< Var(\widehat{\theta}_2).\]
Sea \(X\) una v.a. con media \(\mu_X\) y desviación típica \(\sigma_X\)
Consideremos la mediana \(Me=Q_{0.5}\) de la realización de una m.a.s. de \(X\) como estimador puntual de \(\mu_X\)
Si \(X\) es normal, \[ \begin{array}{l} E(Me)=\mu_X,\\ \displaystyle Var(Me)\approx \frac{\pi}{2} \frac{\sigma_{X}^2}{n}\approx \frac{1.57 \sigma_{X}^2}{n}=1.57\cdot Var(\overline{X}) > Var(\overline{X}). \end{array} \] Por lo tanto, \(Me\) es un estimador no sesgado de \(\mu_X\), pero menos eficiente que \(\overline{X}\).
Si la población es normal, la media muestral \(\bar X\) es el estimador no sesgado más eficiente de la media poblacional \(\mu_X\).
Si la población es Bernoulli, la proporción muestral \(\hat p_X\) es el estimador no sesgado más eficiente de la proporción poblacional \(p_X\).
Si la población es normal, la varianza muestral \(\tilde S^2_X\) es el estimador no sesgado más eficiente de la varianza poblacional \(\sigma_x^2\).
Como hemos visto, si la población es normal, la varianza muestral es el estimador no sesgado más eficiente de la varianza poblacional
El estimador varianza
\[
S_X^2=\frac{(n-1)}{n} \widetilde{S}_X^2
\]
aunque sea más eficiente, tiene sesgo que tiende a \(0\).
Si \(n\) es pequeño (\(\leq 30\) o 40), es mejor utilizar la varianza muestral \(\widetilde{S}_X^2\) para estimar la varianza, ya que el sesgo influye, pero si \(n\) es grande, el sesgo ya no es tan importante y se puede utilizar \(S_X^2\).
Tenemos una población numerada \(1,2,\ldots,N\)
Tomamos una m.a.s. \(x_1,\ldots,x_n\); sea \(m=\max\{x_1,\ldots,x_n\}\).
Ejemplo
Sentados en una terraza de un bar del Paseo Marítimo de Palma hemos anotado el número de licencia de los 40 primeros taxis que hemos visto pasar:
taxis=c(1217,600,883,1026,150,715,297,137,508,134,38,961,538,1154,
314,1121,823,158,940,99,977,286,1006,1207,264,1183,1120,
498,606,566,1239,860,114,701,381,836,561,494,858,187)Supondremos que estas observaciones son una m.a.s. de los taxis de Palma. Vamos a estimar el número total de taxis.
2.5.3 Estimadores máximo verosímiles
¿Cómo encontramos buenos estimadores?
Antes de explicar la metodología, necesitamos una definición previa:
Sea \(X_{1},\ldots X_{n}\) una m.a.s. de \(X\), y sea \(x_1,x_2,\ldots,x_n\) una realización de esta muestra.
La función de verosimilitud de la muestra es la probabilidad condicionada siguiente: \[ \begin{array}{ll} {L(\theta|x_1,x_2,\ldots,x_n)} & := P(x_1,x_2,\ldots,x_n|\theta)=P(X_1=x_1)\cdots P(X_n=x_n) \\ & = f_X(x_1;\theta)\cdots f_X(x_n;\theta). \end{array} \]
Dada la función de verosimilitud \(L(\theta|x_1,\ldots,x_n)\) de la muestra, indicaremos por \(\hat{\theta}(x_1,\ldots,x_n)\) el valor del parámetro \(\theta\) en el que se alcanza el máximo de \(L(\theta|x_1,\ldots,x_n)\). Será una función de \(x_1,\ldots,x_n\).
Supongamos que tenemos una v.a. Bernoulli \(X\) de probabilidad de éxito \(p\) desconocida.
Para cada m.a.s. \(x_1,\ldots,x_n\) de \(X\), sean \(\widehat{p}_x\) su proporción muestral y \(P(x_1,\ldots,x_n\mid p)\) la probabilidad de obtenerla cuando el verdadero valor del parámetro es \(p\).
Dicho en otras palabras, la proporción muestral es un estimador MV de \(p\).
Ejercicio
Demostrar el teorema anterior.
En general, al ser \(\ln\) una función creciente, en lugar de maximizar \(L(\theta|x_1,\ldots,x_n)\), maximizamos \[ \ln(L(\theta|x_1,\ldots,x_n)) \] que suele ser más simple (ya que transforma los productos en sumas, y es más fácil derivar estas últimas).
Sea \(X_{1},\ldots X_{n}\) una m.a.s. de una v.a. Bernoulli \(X\) de parámetro \(p\) (desconocido). Denotemos \(q=1-p\) \[ \begin{array}{c} f_X(1;p)=P(X=1)=p,\quad f_X(0;p)=P(X=0)=q \end{array} \] es a decir, para \(x\in\{0,1\}\), resulta que \(f_X(x;p)=P(X=x)=p^{x} q^{1-x}.\)
La función de verosimilitud es: \[ \begin{array}{l} L(p|x_1,\ldots,x_n) = f_{X}(x_1;p)\cdots f_{X}(x_n;p) = p^{x_{1}}q^{1-x_{1}} \cdots p^{x_{n}}q^{1-x_{n}} \\ = p^{\sum_{i=1}^n x_{i}} q^{\sum_{i=1}^n (1-x_{i})}= p^{\sum_{i=1}^n x_{i}} q^{n-\sum_{i=1}^n x_{i}} =p^{\sum_{i=1}^n x_{i}} (1-p)^{n-\sum_{i=1}^n x_{i}} \end{array} \]
La función de verosimilitud es \[ L(p|x_1,\ldots,x_n) =p^{\sum_{i=1}^n x_{i}} (1-p)^{n-\sum_{i=1}^n x_{i}}=p^{n\overline{x}}(1-p)^{n-n\overline{x}}, \] donde \(\overline{x}=\dfrac{\sum_{i=1}^n x_{i}}{n}\).
Queremos encontrar el valor de \(p\) en el que se alcanza el máximo de esta función (donde \(\overline{x}\) es un parámetro y la variable es \(p\))
Maximizaremos su logaritmo: \[ \ln(L(p|x_1,\ldots,x_n))=n\overline{x}\ln(p)+n(1-\overline{x})\ln(1-p). \]
Derivamos respecto de \(p\): \[ \begin{array}{l} \ln(L(p|x_1,\ldots,x_n))' =n\overline{x}\frac{1}{p}-n(1-\overline{x})\frac{1}{1-p}\\ \qquad =\frac{1}{p(1-p)}\Big((1-p)n\overline{x}-pn(1-\overline{x})\Big) =\frac{1}{p(1-p)}(n\overline{x} -pn) \\ \qquad=\frac{n}{p(1-p)}(\overline{x} -p) \end{array} \] Estudiamos el signo: \[ \ln(L(p|x_1,\ldots,x_n))'\geq 0 \Leftrightarrow \overline{x} -p\geq 0 \Leftrightarrow p\leq\overline{x} \]
Por lo tanto \[ \ln(L(p|x_1,\ldots,x_n))\left\{ \begin{array}{l} \mbox{ creciente hasta $\overline{x}$}\\ \mbox{ decreciente a partir de $\overline{x}$}\\ \mbox{ tiene un máximo en $\overline{x}$} \end{array}\right. \]
El resultado queda demostrado. \(L(\widehat{p}_X|x_1,\ldots,x_n)\geq L(p|x_1,\ldots,x_n)\) para cualquier \(p\).
2.5.4 Algunos estimadores Máximo Verosímiles
\(\widehat{p}_x\) es el estimador MV del parámetro \(p\) de una v.a. Bernoulli.
\(\overline{X}\) es el estimador MV del parámetro \(\theta\) de una v.a. Poisson.
\(\overline{X}\) es el estimador MV del parámetro \(\mu\) de una v.a. normal.
\(S_X^2\) (no \(\widetilde{S}_X^2\)) es el estimador MV del parámetro \(\sigma^2\) de una v.a. normal.
El máximo (no \(\widehat{N}\)) es el estimador MV de la \(N\) en el problema de los taxis.
En una población hay \(N\) individuos, capturamos \(K\), los marcamos y los volvemos a soltar.
Ahora volvemos a capturar \(n\), de los que \(k\) están marcados. A partir de estos datos, queremos estimar \(N\).
Supongamos que \(N\) y \(K\) no han cambiado de la primera a la segunda captura.
La variable aleatoria \(X=\) Un individuo esté marcado es \(Be(p)\) con \(p=\dfrac{K}{N}\).
Si \(X_1,\ldots,X_n\) es la muestra capturada la segunda vez, entonces \(\widehat{p}_X=\frac{k}{n}\).
\(\widehat{p}_X\) es un estimador máximo verosímil \(p\). Por tanto, estimamos que: \[ \dfrac{K}{N}=\dfrac{k}{n}\Rightarrow N=\frac{n\cdot K}{k} \]
Por lo tanto, el estimador \[ \widehat{N}=\frac{n\cdot K}{k} \] maximiza la probabilidad de la observación \(k\) marcados de \(n\) capturados, por lo que \(\hat{N}\) es el estimador máximo verosímil de \(N\).
Ejercicio
Supongamos que hemos marcado 15 peces del lago, y que en una captura, de 10 peces, hay 4 marcados. ¿Cuántos peces estimamos que contiene el lago?
El número de peces estimados del lago será: \[ \widehat{N}=\frac{15\cdot 10}{4}=37.5 \] Estimamos que habrá entre 37 y 38 peces en el lago.
El estimador \[ \widehat{N}=\frac{n\cdot K}{k} \] es sesgado, con sesgo que tiende a \(0\).
El estimador de Chapman \[ \widehat{N}=\frac{(n+1)\cdot (K+1)}{k+1}-1, \] es menos segado para muestras pequeñas, y no sesgado si \(K+n\geq N\) (pero no máximo verosímil).
2.6 Estimación puntual con R
2.6.1 La función fitdistr
Para obtener estimaciones puntuales con R hay que usar la función fitdistr del paquete MASS:
donde
xes la muestra, un vector numérico.El valor de
densfunha de ser el nombre de la familia de distribuciones:"chi-squared","exponential","f","geometric","lognormal","normal"y"poisson".Si
fitdistrno dispone de una fórmula cerrada para el estimador máximo verosímil de algún parámetro, usa un algoritmo numérico para aproximarlo que requiere de un valor inicial para arrancar. Este valor (o valores) se puede especificar igualando el parámetrostarta unalistcon cada parámetro a estimar igualado a un valor inicial.
Estimación del parámetro \(\lambda\) de una variable de Poisson.
Consideramos la muestra siguiente de tamaño 50 de una variable de Poisson de parámetro \(\lambda =5\):
## [1] 5 4 4 5 3 4 1 4 6 3 7 7 3 5 4 8 4 4 6 3 6 4 6 11 4
## [26] 7 5 2 8 3 5 4 1 5 6 4 7 7 3 4 6 10 5 4 2 9 1 5 2 2Vamos a estimar el valor del parámetro \(\lambda\) a partir de la muestra anterior.
Para estimar \(\lambda\) usamos la función fitdistr:
## lambda
## 4.76000000
## (0.30854497)La función fitdistr nos ha dado el siguiente valor de \(\lambda\): 4.76, valor que se aproxima al valor real de \(\lambda =5\), con un error típico de 0.30854497.
Recordemos que el estimador máximo verosímil de \(\lambda\) es \(\overline{X}\) con error típico \(\frac{\sqrt{\lambda}}{\sqrt{n}}\). Veamos si la función fitdistr nos ha mentido:
## [1] 4.76## [1] 0.30854497Comprobamos que los valores anteriores coinciden con los dados por la función.
¿Qué estimaciones hubiésemos obtenido de la media \(\mu\) y la desviación típica \(\sigma\) si suponemos que la muestra anterior es normal?
## mean sd
## 4.76000000 2.18686991
## (0.30927011) (0.21868699)Dichos valores coinciden con la media muestral \(\overline{X}\) y la desviación típica “verdadera” de la muestra considerada:
## [1] 2.18686992.7 Guía rápida
fitdistrdel paquete MASS, sirve para calcular los estimadores máximo verosímiles de los parámetros de una distribución a partir de una muestra. Parámetros principales:densfun: el nombre de la familia de distribuciones, entre comillas.start: permite fijar el valor inicial del algoritmo numérico para calcular el estimador, si la función lo requiere.