Tema 3 Intervalos de confianza

Una estimación por intervalos de un parámetro poblacional es una regla para calcular, a partir de una muestra, un intervalo en el que, con una cierta probabilidad (nivel de confianza), se encuentra el valor verdadero del parámetro.

Estas reglas definirán, a su vez, estimadores.

Ejemplo

Hemos escogido al azar 50 estudiantes de grado de la UIB, hemos calculada sus notas medias de las asignaturas del primer semestre, y la media de estas medias ha sido un 6.3, con una varianza muestral de 1.8.

Determinar un intervalo del que podamos afirmar con probabilidad 95% que contiene la media real de las notas medias de los estudiantes de grado de la UIB este primer semestre.

Ejemplo

En un experimento en el que se ha medido la tasa oficial de alcoholemia en sangre a 40 varones (sobrios) después de tomar 3 cañas de cerveza de 330 ml. La media y la desviación típica de esta tasa han sido \[ \overline{x}=0.7,\quad \widetilde{s}=0.1. \] Determinar un intervalo que podamos afirmar con probabilidad 95% que contiene la tasa de alcoholemia media en sangre de una varón después de beber 3 cañas de cerveza de 330 ml.

Intervalo de confianza. Dado un parámetro \(\theta\), el intervalo \((A,B)\) es un intervalo de confianza del \((1-\alpha)\cdot 100\%\) para al parámetro \(\theta\) cuando \[ P(A<\theta<B)=1-\alpha. \] El valor \((1-\alpha)\cdot 100\%\) (o contiene solo el \(1-\alpha\)) recibe el nombre de nivel de confianza.

El valor \(\alpha\) recibe el nombre de nivel de significación.

Por defecto, buscaremos intervalos bilaterales tales que la cola de probabilidad sobrante \(\alpha\) se reparta por igual a cada lado del intervalo: \[ P(\theta<A)=P(\theta>B)=\frac{\alpha}{2} \]

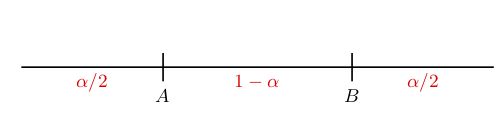
Por ejemplo, para buscar un intervalo de confianza \((A,B)\) del \(95\%\), buscaremos valores \(A,B\) de manera que \[ P(\theta<A)=0.025\quad\mbox{ y }\quad P(\theta>B)=0.025. \]

3.1 Intervalos de confianza para el parámetro \(\mu\) de una población normal

3.1.1 Intervalos de confianza para el parámetro \(\mu\) de una población normal con \(\sigma\) conocida

Sea \(X\) una v.a. normal con media poblacional \(\mu\) desconocida y desviación típica poblacional \(\sigma\) conocida (a la práctica, usualmente, estimada en un experimento anterior)

Sea \(X_1,\ldots,X_n\) una m.a.s. de \(X\), con media muestral \(\overline{X}\)

Queremos determinar un intervalo de confianza para a \(\mu\) con un cierto nivel de confianza (digamos, \(97.5\%\), \(\alpha =0.025\)): un intervalo \((A,B)\) tal que \[ P(A<\mu<B)=1-\alpha = 0.975 \]

Bajo estas condiciones, sabemos que \[ Z=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}} \] sigue una distribución normal estándar.

Comencemos calculando un intervalo centrado en \(0\) en el que \(Z\) tenga probabilidad \(0.975\): \[ \begin{array}{l} 0.975= P(-\delta<Z<\delta)=F_{Z}(\delta)-F_{Z}(-\delta)= 2 F_{Z}(\delta)-1\\ F_{Z}(\delta)=\dfrac{1.975}{2}=0.9875\Rightarrow \delta=\mbox{qnorm}(0.9875)=2.2414. \end{array} \]

Por lo tanto \[ P(-2.2414<Z<2.2414)=0.975 \] Substituyendo \(Z=\dfrac{\overline{X}-\mu}{\sigma/\sqrt{n}}\): \[ \begin{array}{c} P\left(-2.2414<\dfrac{\overline{X}-\mu}{\sigma/\sqrt{n}} <2.2414\right)=0.975\\ P\left(\overline{X} -2.2414 \dfrac{\sigma}{\sqrt{n}}< \mu< \overline{X}+ 2.2414\dfrac{\sigma}{\sqrt{n}}\right)=0.975 \end{array} \]

Por lo tanto, la probabilidad que la media poblacional \(\mu\) de \(X\) se encuentre dentro del intervalo \[ \left(\overline{X} -2.2414 \frac{\sigma}{\sqrt{n}}, \overline{X}+ 2.2414\frac{\sigma}{\sqrt{n}} \right) \] es \(0.975\): es un intervalo de confianza del \(97.5\%\).

Además tenemos que está centrado en \(\overline{X}\): el 0.025 de probabilidad restante está repartido por igual en los dos extremos del intervalo.

Como estimador: un \(97.5\%\) de las veces que tomemos una muestra de tamaño \(n\) de \(X\), el verdadero valor de \(\mu\) caerá dentro de este intervalo

Para una muestra concreta: la probabilidad de que, si una media \(\mu\) poblacional ha producido esta muestra, entonces esté en este intervalo concreto, es del \(97.5\%\).

En ocasiones lo entenderemos como: La probabilidad de que \(\mu\) esté en este intervalo es del \(97.5\%\).

Pero la frase anterior es mentira (es un abuso de lenguaje): La \(\mu\) concreta es un valor fijo, por lo tanto que pertenezca o no a este intervalo concreto tiene probabilidad 1 (si pertenece) y 0 (si no pertenece).

Teorema. Sea \(X\sim N(\mu,\sigma)\) con \(\mu\) desconocida y \(\sigma\) conocida.

Tomamos una m.a.s. de \(X\) de tamaño \(n\), con media \(\overline{X}\).

Un intervalo de confianza del \((1-\alpha)\cdot 100\%\) para \(\mu\) es \[ \left(\overline{X} -z_{1-\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}, \overline{X}+z_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}} \right) \] donde \(z_{1-\frac{\alpha}{2}}\) es el \((1-\frac{\alpha}{2})\)-cuantil de la normal estándar \(Z\) (es decir, \(z_{1-\frac{\alpha}{2}}=F_Z^{-1}(1-\frac{\alpha}{2})\), o \(P(Z\leq z_{1-\frac{\alpha}{2}})=1-\frac{\alpha}{2}\)).

Si \(X\) es normal con \(\sigma\) conocida, un intervalo de confianza I.C. para \(\mu\) de población normal con \(\sigma\) conocida \(\mu\) del \((1-\alpha)\cdot 100\%\) es \[ \overline{X} \pm z_{1-\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}:=\left(\overline{X} -z_{1-\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}, \overline{X}+z_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}. \right) \] Observad que está centrado en \(\overline{X}\).

La tabla siguiente muestra los cuantiles más usados:

Confianza \(1-\alpha\)	Significación \(\alpha\)	Cuantil \(z_{1-\frac{\alpha}{2}}\)
0.90	0.1	1.645
0.95	0.05	1.96
0.975	0.025	2.241

3.1.2 Simulación de intervalos de confianza

Ejemplo

A continuación vamos a simular el funcionamiento de un intervalo de confianza para una distribución normal.

Consideramos una población de \(10^6\) valores de una distribución normal de parámetros \(\mu =1.5\) y \(\sigma =1\):

set.seed(1012)
mu=1.5; sigma=1; alpha=0.05
Población=rnorm(10^6,mu,sigma)

Vamos a generar 100 muestras aleatorias simples de tamaño 50 de dicha población para posteriormente generar un intervalo de confianza al \(95\%\) de confianza para el parámetro \(\mu\) para cada muestra.

Primero definiremos una función para que, dada una muestra, un valor \(\sigma\) y un nivel de significación \(\alpha\) nos genere el intervalo correspondiente para el parámetro \(\mu\) al nivel de confianza \(100\cdot (1-\alpha)\%\). La llamaremos ICZ:

ICZ=function(x,sigma,alpha){
  c(mean(x)-qnorm(1-alpha/2)*sigma/sqrt(length(x)), 
  mean(x)+qnorm(1-alpha/2)*sigma/sqrt(length(x)))}

Usando la función replicate de R generamos las muestras y los intervalos de confianza correspondientes usando la función anterior:

set.seed(2)
M=replicate(100,ICZ(sample(Población,50,replace=T),
 sigma,alpha))

El objeto \(M\) de R es una matriz de 2 filas y 100 columnas donde la columna \(i\)-ésima representa el intervalo de confianza para la muestra \(i\)-ésima generada.

Finalmente vamos a dibujar todos los intervalos anteriores y resaltaremos en color rojo aquéllos en los que el parámetro \(\mu =1.5\) no esté en ellos. Esperamos que haya aproximadamente 5 en los que esta condición falle.

El resultado se muestra en la figura siguiente:

plot(1:10,type="n",xlim=c(1.2,1.8),ylim=c(0,100),
xlab="Valores",ylab="Replicaciones")
seg.int=function(i){color="grey";
  if((mu<M[1,i]) | (mu>M[2,i])){color = "red"}
  segments(M[1,i],i,M[2,i],i,col=color,lwd=3)}
invisible(sapply(1:100,FUN=seg.int))
abline(v=mu,lwd=3)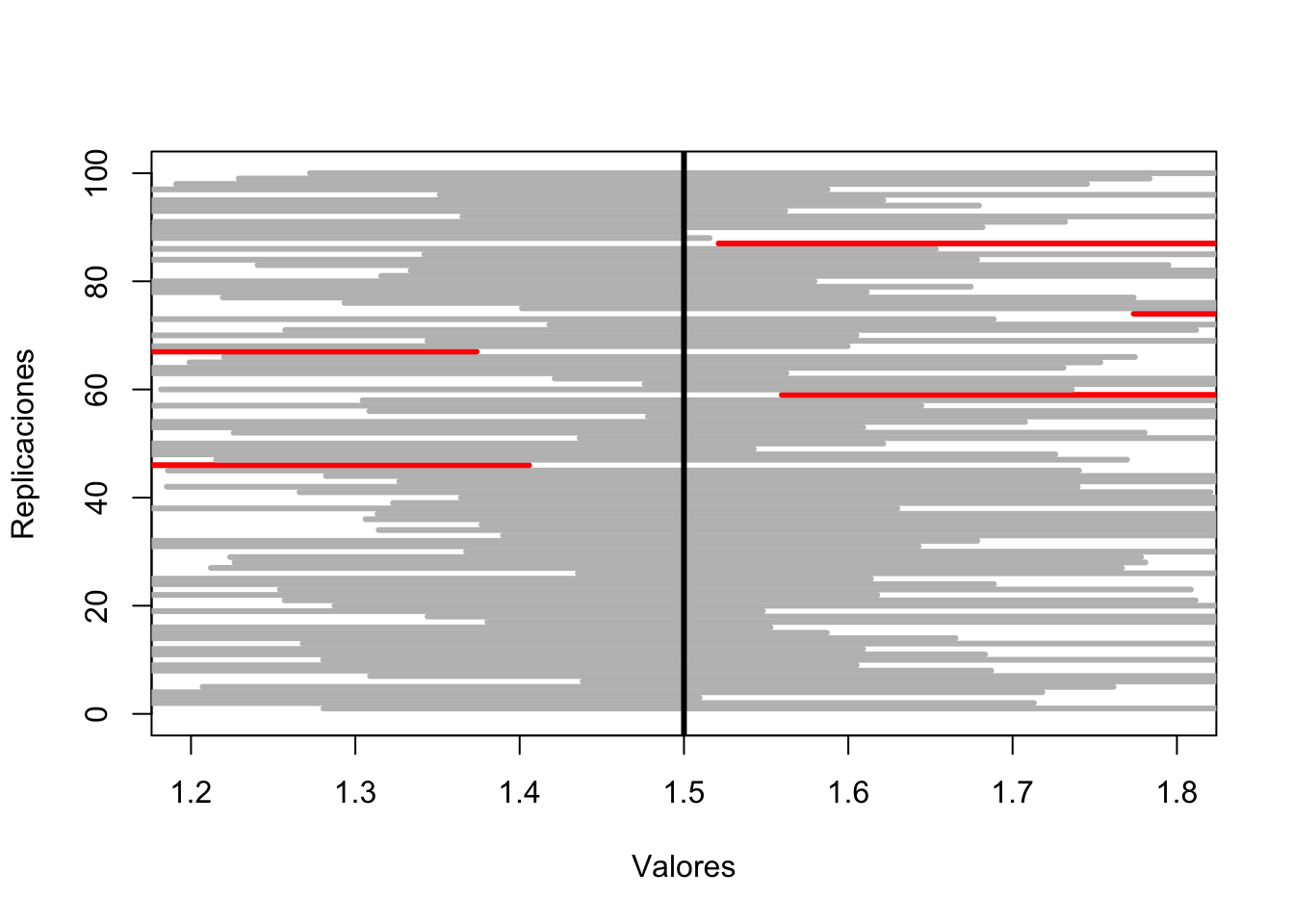

3.1.3 Interpretación del intervalo de confiaza.

¡Atención! De media, un \(\alpha\cdot 100\%\) de las veces, un intervalo de confianza del \((1-\alpha)\cdot 100\%\) no contendrá el valor real del parámetro.

Por ejemplo, de media, un \(5\%\) de las veces un intervalo de confianza del \(95\%\) no contendrá el valor real del parámetro.

Ejercicio

Tomamos una m.a.s. de tamaño \(n=16\) de una v.a. normal con \(\sigma=4\) y \(\mu\) desconocida. La media de la m.a.s. es \(\overline{x}=20\).

Calculad un intervalo de confianza del \(97.5\%\) para \(\mu\) de una población normal con \(\sigma\) conocida.

El valor de \(\alpha\) será \(\alpha = 1-0.975=0.025\). El intervalo de confianza será: \[ \begin{array}{ll} \left(\overline{x}-z_{1-\frac{\alpha}{2}}\cdot\frac{\sigma}{\sqrt{n}},\overline{x}+z_{1-\frac{\alpha}{2}}\cdot\frac{\sigma}{\sqrt{n}}\right) & \\ = \left( 20-2.241\cdot \frac{4}{\sqrt{16}} , 20+2.241\cdot \frac{4}{\sqrt{16}} \right)&\\ =(17.759,22.241).& \end{array} \]

La probabilidad de que, si una media \(\mu\) poblacional ha producido esta muestra, entonces esté en este intervalo concreto, es del \(97.5\%\).

Ejemplo del procesador Intel Core

Queremos analizar un sensor que mide la temperatura de un procesador en grados centígrados, en concreto un Intel Core i7-2600K, que tiene como temperatura normal de \(32^{\circ}\) a \(40^{\circ}\). Para saber si está bien calibrado, diseñamos un experimento en el que ponemos el procesador en las mismas condiciones y tomamos una muestra de 40 valores de su temperatura.

Los resultados son los siguientes:

temperatura=c(36,35,38,38,36,37,38,36,37,36,
              37,37,34,38,35,37,36,36,34,38,
              36,37,35,35,35,35,36,36,36,35,
              36,35,34,34,37,37,35,36,34,36)

Supongamos que las medidas de nuestro sensor siguen una distribución normal con varianza poblacional conocida \(\sigma^2=1.44\). Calculad un intervalo de confianza del \(90\%\) para al resultado medio de la temperatura del procesador.

Tenemos las siguientes condiciones:

• Población normal con \(\sigma=\sqrt{1.44}=1.2\) conocida.
• Muestra aleatoria simple de tamaño \(n=40\).
• Media de la muestra \(\overline{x}=35.975\).
• \(1-\alpha=0.9\Rightarrow \alpha=0.1\Rightarrow 1-\frac{\alpha}{2}=0.95\).
• \(z_{0.95}\approx 1.645.\)

Aplicamos la fórmula \(\overline{X}\pm z_{1-\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\) con \(\overline{x}=35.975, z_{0.95}=1.645, \sigma=1.2, n=40.\)

Obtenemos que el intervalo de confianza del \(90\%\) es

\[ 35.975\pm 1.645\cdot\frac{1.2}{\sqrt{40}} = (35.663 , 36.287). \]

Amplitud del intervalo de confianza. La amplitud \(A\) del intervalo de confianza a un nivell \(100\cdot (1-\alpha)\%\) de confianza será: \[ A = \overline{X}+ z_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}-\Big(\overline{X} -z_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\Big)= 2\cdot z_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}. \]

Error máximo cometido. El error máximo, al nivel de confianza \(100\cdot (1-\alpha)\%\), que cometemos al estimar \(\mu\) por \(\overline{X}\) es la mitad de la amplitud,

\[ z_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}. \]

Propiedades

• La amplitud del intervalo de confianza para el parámetro \(\mu\) de una población normal con \(\sigma\) conocida, \(n\) y \(\alpha\) fijos crece, si \(\sigma\) crece.

• La amplitud del intervalo de confianza para el parámetro \(\mu\) de una población normal con \(\sigma\) conocida y \(\alpha\) fijo decrece, si \(n\) crece.

• La amplitud del intervalo de confianza para el parámetro \(\mu\) de una población normal con \(\sigma\) conocida y \(n\) fijo crece, si \(1-\alpha\) crece, o si \(\alpha\) decrece.

Problema: hallar el tamaño \(n\) mínimo de la muestra para asegurar que el intervalo de confianza para \(\mu\) al nivel de confianza \((1-\alpha)\) tenga una amplitud prefijada máxima \(A_0\) (o un error máximo \(A_0/2\)).

Resolución: usando que la amplitud máxima tiene que ser \(A_0\) tenemos que se tiene que verificar \(A_0\geq 2z_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\).

Despejando \(n\) de la expresión anterior, tendremos que el tamaño de la muestra mínimo será: \[ n\geq \left( 2 z_{1-\frac{\alpha}{2}}\frac{\sigma}{A_0}\right)^2. \]

Ejemplo

Recordemos que las medidas de nuestro sensor de temperatura seguían una distribución normal con varianza poblacional conocida \(\sigma^2=1.44\), \(\sigma=1.2\).

¿Cuántas medidas tendríamos que tomar para obtener la temperatura media con un error máximo de \(0.05^{\circ}\) al nivel de confianza del \(90\%\)?

Nos dicen que \(\frac{A_0}{2}=0.05\), o sea, \(A_0=0.1\). Usando la expresión anterior, tendremos que el número de medidas mínimo \(n\) que tendríamos que tomar será:

\[ n=\left\lceil \left( 2 z_{1-\frac{\alpha}{2}}\frac{\sigma}{A_0} \right)^2\right\rceil \]

donde \(z_{1-\frac{\alpha}{2}}=1.645,\ \sigma=1.2\). Obtenemos \[ n= \left\lceil \left(2\cdot 1.645\cdot \frac{1.2}{0.1}\right)^2 \right\rceil= \lceil 1558.393\rceil = 1559. \]

3.1.4 Intervalos de confianza para el parámetro \(\mu\) de una población normal con \(\sigma\) desconocida

Recordemos que para hallar el intervalo de confianza para el parámetro \(\mu\) de una población normal, era clave la variable aleatoria \(\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}.\)

El problema es que ahora no la podemos usar al no conocer \(\sigma\).

Lo que haremos será sustituir la desviación típica poblacional \(\sigma\) por la desviación típica muestral \(\widetilde{S}_{X}\) y nos quedará: \(\frac{\overline{X}-\mu}{\widetilde{S}_{X}/\sqrt{n}},\) donde \(\overline{X}\) es la media muestral y \(n\), el tamaño de la muestra.

La distribución de la variable anterior \(\frac{\overline{X}-\mu}{\widetilde{S}_{X}/\sqrt{n}},\) no será normal sino \(t\) de Student con \(n-1\) grados de libertad como nos dice el teorema siguiente:

Teorema. Sea \(X\sim N(\mu,\sigma)\). Sea \(X_1,\ldots,X_n\) una m.a.s. de \(X\), con media \(\overline{X}\) y desviación típica muestral \(\widetilde{S}_{X}\)

En estas condiciones, la v.a. \(t=\frac{\overline{X}-\mu}{\widetilde{S}_{X}/\sqrt{n}},\) sigue una distribución \(t\) de Student con \(n-1\) grados de libertad, \(t_{n-1}\).

Distribución \(t\) de Student

La distribución \(t\) de Student con \(\nu\) grados de libertad, \(t_{\nu}\) tiene como función de densidad \[ f_{t_\nu}(x) = \frac{\Gamma(\frac{\nu+1}{2})} {\sqrt{\nu\pi}\,\Gamma(\frac{\nu}{2})} \Big(1+\frac{x^2}{\nu} \Big)^{-\frac{\nu+1}{2}}, \] donde \(\Gamma(x)=\int_{0}^{\infty} t^{x-1}e^{-t}\, dt\) si \(x> 0\).

Propiedades

• \(E(t_{\nu})=0\) si \(\nu>1\) y \(Var(t_{\nu})=\dfrac{\nu}{\nu-2}\) si \(\nu>2\).
• Su función de distribución es simétrica respecto de \(E(t_{\nu})=0\) (como la de una \(N(0,1)\)): \[ P(t_{\nu}\leq -x)=P(t_{\nu}\geq x)=1-P(t_{\nu}\leq x). \]
• Si \(\nu\) es grande, su distribución es aproximadamente la de \(N(0,1)\) (pero con más varianza: un poco más aplastada)

Gráficas de las densidades de diferentes distribuciones \(t\) de Student junto con la densidad de la \(N(0,1)\):

Indicaremos con \(t_{\nu,q}\) el \(q\)-cuantil de una v.a. \(X\) que sigue una distribución \(t_\nu\): \[ P(X\leq t_{\nu,q})=q \]

Por simetría, \(t_{\nu,q}=-t_{\nu,1-q}\).

Consideremos la situación siguiente:

• \(X\) una v.a. normal con \(\mu\) y \(\sigma\) desconocidas.

• \(X_1,\ldots,X_n\) una m.a.s. de \(X\) de tamaño \(n\), con media \(\overline{X}\) y varianza muestral \(\widetilde{S}_X^2\).

Intervalo de confianza para el parámetro \(\mu\). En estas condiciones, un intervalo de confianza del \((1-\alpha)\cdot 100\%\) para el parámetro \(\mu\) de una población normal con \(\sigma\) desconocida es \[ \left( \overline{X}-t_{n-1,1-\frac{\alpha}{2}} \frac{\widetilde{S}_{X}}{\sqrt{n}}, \overline{X}+t_{n-1,1-\frac{\alpha}{2}}\frac{\widetilde{S}_{X}}{\sqrt{n}} \right). \]

Ejemplo 3D-print

La empresa 3D-print ofrece una impresora industrial de papel en color de alta capacidad. En su publicidad afirma que sus cartuchos imprimen una media de 500 mil copias con la especificación:

`Ficha técnica: Muestra de tamaño n=100, población aproximadamente normal, nivel de confianza del \(90\%\).

La OCU (asociación de consumidores) desea comprobar estas afirmaciones y su laboratorio toma una muestra aleatoria de tamaño \(n=24\), obteniendo una media de \(\overline{x}=518\) mil impresiones y una desviación típica muestral \(\widetilde{s}=40\) mil.

Con esta muestra ¿la media poblacional anunciada por fabricante cae en el intervalo de confianza del \(90\%\)?

Hay que calcular el intervalo de confianza para la \(\mu\) de una población normal con \(\sigma\) desconocida \(\mu\) con los valores siguientes: \(n=24, \overline{x}=518, \widetilde{s}=40, \alpha=0.1\).

Dicho intervalo será el siguiente:

\[ \begin{array}{ll} \left(\overline{x}-t_{23,0.95} \frac{\widetilde{s}}{\sqrt{n}}, \overline{x}+t_{23,0.95} \frac{\widetilde{s}}{\sqrt{n}}\right) & \\ =\left(518.000-1.714 \frac{40.000}{\sqrt{24}}, 518.000 + 1.714 \frac{40.000}{\sqrt{24}}\right) \\ = \left( 5.04006298\times 10^{5},\qquad 5.31993702\times 10^{5}\right)&. \end{array} \] Observamos que no contiene a 500.000 (¡pero se equivoca a favor del consumidor!)

Observaciones:

• El intervalo de confianza obtenido está centrado en \(\overline{X}\)

• La fórmula \(\left( \overline{X}-t_{n-1,1-\frac{\alpha}{2}} \frac{\widetilde{S}_{X}}{\sqrt{n}}, \overline{X}+t_{n-1,1-\frac{\alpha}{2}}\frac{\widetilde{S}_{X}}{\sqrt{n}} \right)\) nos da el intervalo de confianza para \(\mu\) en una población normal con \(\sigma\) desconocida. La expresión anterior se puede utilizar cuando \(X\) es normal y \(n\) cualquiera

• Si \(n\) es grande \(t_{n-1,1-\frac{\alpha}{2}}\approx z_{1-\frac{\alpha}{2}}\) y podemos aproximar el intervalo de confianza anterior mediante la expresión siguiente: \[ \left( \overline{X}-z_{1-\frac{\alpha}{2}} \frac{\widetilde{S}_{X}}{\sqrt{n}}, \overline{X}+z_{1-\frac{\alpha}{2}}\frac{\widetilde{S}_{X}}{\sqrt{n}} \right) \]

Consideremos la situación siguiente:

• \(X\) una v.a. cualquiera con media poblacional \(\mu\) desconocida y desviación típica \(\sigma\) desconocida.

• \(X_1,\ldots,X_n\) una m.a.s. de \(X\), con media \(\overline{X}\).

• \(n\) es grande (pongamos que \(n\geq 40\))

3.1.5 Intervalos de confianza para el parámetro \(\mu\) de una población cualquiera con \(\sigma\) conocida y tamaño muestral grande

En estas condiciones, usando el Teorema Central del Límite \(\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\approx N(0,1)\).

Teorema. En las condiciones anteriores, podemos tomar como intervalo de confianza del \((1-\alpha)\cdot 100\%\) de confianza para el parámetro \(\mu\) de una población cualquiera con \(\sigma\) conocida la expresión siguiente: \[ \left(\overline{X}-z_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}, \overline{X}+z_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\right) \]

Si la \(\sigma\) es desconocida, podemos aplicar el Teorema anterior sustituyendo \(\sigma\) por \(\widetilde{S}_X\):

Teorema. En las condiciones anteriores, podemos tomar como intervalo de confianza del \((1-\alpha)\cdot 100\%\) de confianza para el parámetro \(\mu\) de una población cualquiera con \(\sigma\) desconocida la expresión siguiente: \[ \left(\overline{X}-z_{1-\frac{\alpha}{2}}\frac{\widetilde{S}_X}{\sqrt{n}}, \overline{X}+z_{1-\frac{\alpha}{2}}\frac{\widetilde{S}_X}{\sqrt{n}}\right) \]

Ejercicio

Se ha tomado una muestra del tiempo de visualización de vídeo semanal en horas de 1000 usuarios de un canal de videos por internet. Se ha obtenido una media muestral de 9.5 horas/semana con una desviació típica muestral de 0.5 horas/semana.

Calculad un intervalo de confianza del 95% para la media poblacional del número de horas visualizadas por semana supuesto que sigue aproximadamente una población normal con \(\sigma\) desconocida.

Como \(n=1000\) es grande, podemos utilizar la expresión siguiente para hallar el intervalo de confianza: \[\left(\overline{x}-z_{1-\frac{\alpha}{2}}\frac{\widetilde{s}}{\sqrt{n}}, \overline{x}+z_{1-\frac{\alpha}{2}}\frac{\widetilde{s}}{\sqrt{n}}\right),\] donde \(\overline{x}=9.5,\ \widetilde{s}=0.5,\ \alpha=0.05,\ z_{1-\frac{\alpha}{2}}=1.96.\) El intervalo de confianza será, pues:

media=9.5
sd=0.5
n=1000
alpha=0.5
cuantil=qnorm(1-alpha/2)
(extremo.izquierdo=round(media-cuantil*sd/sqrt(n),3))

## [1] 9.489

(extremo.derecho=round(media+cuantil*sd/sqrt(n),3))

## [1] 9.511

Podemos afirmar con un 95% de confianza que la media poblacional de vídeo consumido en horas por semana está entre \(9.489\) y \(9.511\) horas/semana.

Amplitud del intervalo de confianza.

La amplitud de \(\left(\overline{X}-z_{1-\frac{\alpha}{2}}\frac{\widetilde{S}_X}{\sqrt{n}}, \overline{X}+z_{1-\frac{\alpha}{2}}\frac{\widetilde{S}_X}{\sqrt{n}}\right)\) es \(A=2z_{1-\frac{\alpha}{2}}\frac{\widetilde{S}_X}{\sqrt{n}}\).

Para determinar \(n\) (grande) que dé cómo máximo una amplitud \(A\) prefijada, necesitamos \(\widetilde{S}_X\), que depende de la muestra.

Soluciones:

• Si sabemos la desviación típica poblacional \(\sigma\), la utilizaremos en lugar de \(\widetilde{S}_X\).
• Si hemos tomado una muestra previa (piloto), emplearemos la desviación típica muestral de esta muestra piloto para estimar \(\sigma\).

De una población \(X\) hemos tomado una m.a.s. (piloto) que ha tenido una desviación típica muestral \(\widetilde{s}_{piloto}\).

Estimaremos que el tamaño mínimo \(n\) de una m.a.s. de \(X\) que dé un intervalo de confianza I.C. para \(\mu\) de una población normal con \(\sigma\) desconocida de nivell de confianza \(1-\alpha\) y amplitud máxima \(A_0\) es \[ n=\left\lceil \Big(2z_{1-\frac{\alpha}{2}}\frac{\widetilde{s}_{piloto}}{A_0}\Big)^2\right\rceil \]

Ejercicio

Queremos estimar la estatura media de los estudiantes de la UIB. Queremos obtener un intervalo de confianza del 99% con una precisión máxima de 1 cm. En una muestra piloto de 25 estudiantes, obtuvimos que \[\overline{x} = 170\mbox{ cm}, \widetilde{s}=10\mbox{ cm}.\]

¿Basándonos en estos datos, cuál es el tamaño necesario de la muestra para poder alcanzar nuestro objetivo?

Con una precisión de 1 cm. tendremos que la amplitud máxima será el doble: 2 cm.

Por tanto el tamaño necesario de la muestra será:

alpha=0.01
cuantil = qnorm(1-alpha/2)
amplitud = 2
s.piloto = 10
(n.minimo = ceiling((2*cuantil*s.piloto/amplitud)^2))

## [1] 664

Si queremos, podemos estudiar estos conceptos directamente utilizando la función t.test de R:

t.test(X,conf.level=...)$conf.int

donde conf.level es el nivel de confianza \(1-\alpha\) en tanto por uno. Su valor por defecto es \(1-\alpha =0.95\).

Ejemplo tabla de datos iris

Hallemos un intervalo de confianza para la media de la longitud del pétalo para una muestra de 30 flores de la tabla de datos iris.

• En primer lugar elegimos las flores de la muestra:

set.seed(1000)
muestra.iris = sample(1:150,30,replace=TRUE)

A continuación calculamos las longitudes del pétalo de las flores de nuestra muestra:

long.pétalo.muestra = iris[muestra.iris,]$Petal.Length

Un intervalo de confianza al 95% de confianza para las longitudes del pétalo sería:

t.test(long.pétalo.muestra,conf.level=0.95)$conf.int

## [1] 2.9865374 4.1067959
## attr(,"conf.level")
## [1] 0.95

3.1.6 Experimento sobre la “confianza”

Experimento

Vamos a comprobar con un experimento qué papel juega la “confianza” en los intervalos de confianza.

Vamos a generar al azar una Población de 10000000 (\(10^7\)) “individuos” con distribución normal estándard. Vamos a tomar 200 muestras aleatorias simples de tamaño 50 de esta población y calcularemos el intervalo de confianza para la media poblacional usando dicha fórmula.

Finalmente, contaremos cuántos de estos intervalos de confianza contienen la media de la población. Fijaremos la semilla de aleatoriedad para que el experimento sea reproducible y podáis comprobar que no hacemos trampa.

En primer lugar, generamos la población de valores:

set.seed(2020)
valores.población=rnorm(10^7)

Seguidamente, hallamos la media poblacional:

(mu=mean(valores.población))

## [1] -2.9033996e-06

Para hallar 200 muestras, usaremos la función replicate de R que nos permite ejecutar una misma función las veces que le indiquemos:

muestras=replicate(200, sample(valores.población,50,replace=TRUE))

De esta forma muestras es una matriz de 50 filas y 200 columnas donde cada fila representa una muestra.

A continuación, Vamos a aplicar a cada una de estas muestras la función t.test para calcular un intervalo de confianza del 95% y luego contaremos los aciertos, es decir, cuántos de ellos contienen la media poblacional.

Primero definimos la función IC.t que nos da el intervalo de confianza para la media dada una muestra X:

IC.t= function(X, confianza=0.95){
  t.test(X, conf.level=confianza)$conf.int
  }

En segundo lugar, calculamos los 200 intervalos de confianza para nuestras 200 muestras usando la función apply de R:

ICs= apply(muestras,FUN=IC.t,MARGIN=2)

En tercer lugar, miramos cuántos de los intervalos anteriores contienen la media poblacional mu:

Aciertos=length(which((mu>=ICs[1,]) & (mu<=ICs[2,])))
Aciertos

## [1] 195

Hemos acertado 195 veces, o sea, el 97.5% de las veces. Es una buena aproximación del valor 95%, que era el esperado.

Para visualizar mejor los aciertos, vamos a dibujar los intervalos apilados en un gráfico, donde aparecerán en azul claro los que aciertan y en rojo los que no aciertan.

plot(1,type="n",xlim=c(-0.8,0.8),ylim=c(0,200),xlab="Valores",
     ylab="Repeticiones",main="")

seg.int=function(i){
  color="light blue"
  if((mu<ICs[1,i]) | (mu>ICs[2,i])){
    color = "red"
  }
  segments(ICs[1,i],i,ICs[2,i],i,col=color,lwd=2)
}

sapply(1:200,FUN=seg.int)
abline(v=mu,lwd=2)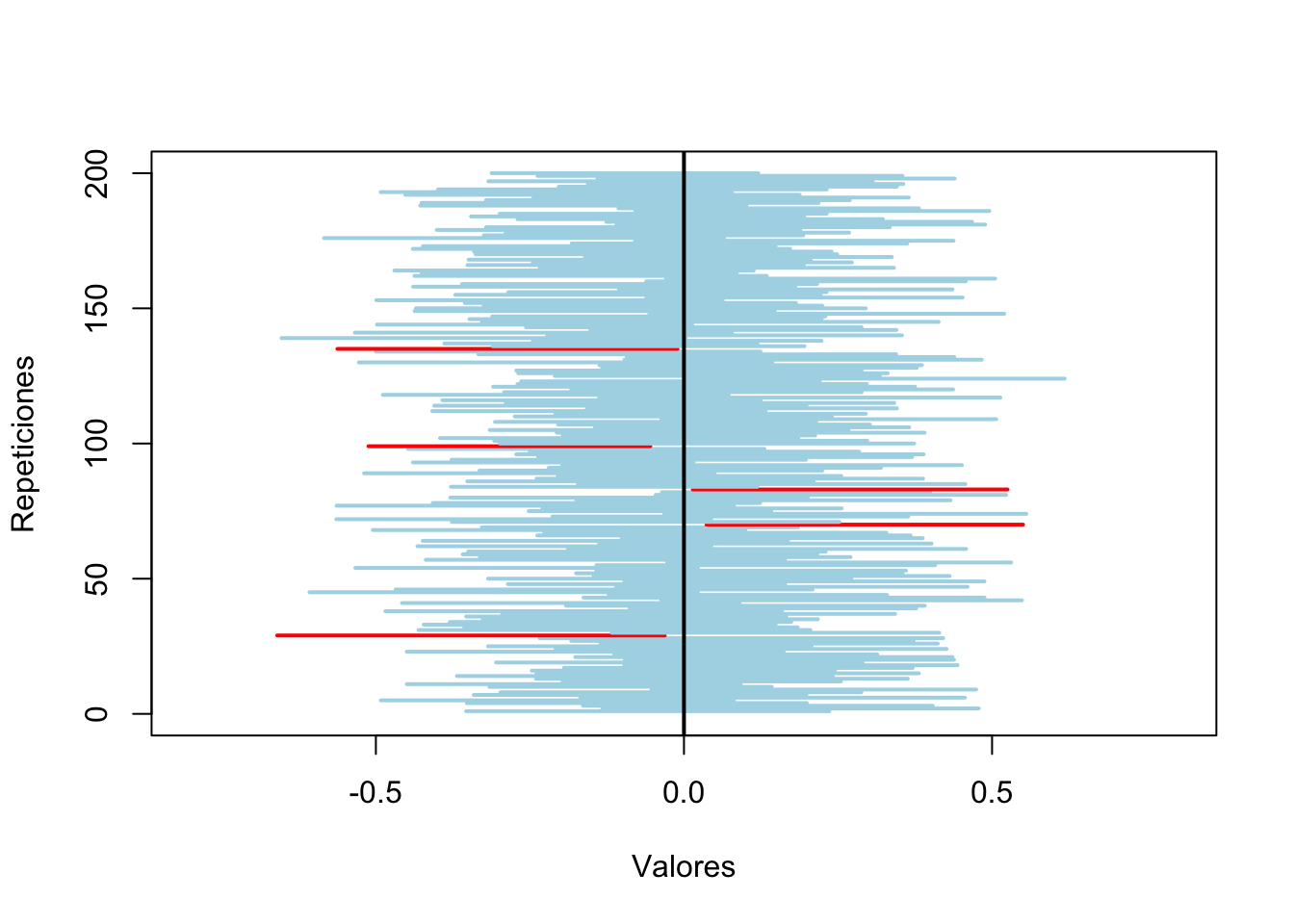

3.2 Intervalos de confianza para el parámetro \(p\) de una población de Bernoulli

3.2.1 Método “exacto” o de Clopper-Pearson

Consideremos la situación siguiente:

• \(X\) una v.a. Bernoulli con \(p\) desconocido.
• \(X_1,\ldots,X_n\) una m.a.s. de \(X\), con número de éxitos \(x\) y por lo tanto la frecuencia relativa de éxitos es \(\widehat{p}_{X}=x/n\).

En este caso, la distribución de la variable \(Y=\)“número de éxitos en la muestra” es binomial de parámetros \(n\) y \(p\), \(Y\) es \(B(n,p)\)

Definición. Un intervalo de confianza \((p_0,p_1)\) del \((1-\alpha)100\%\) nivel de confianza para \(p\) de una población \(X\) de Bernoulli se obtiene encontrando el \(p_0\) más grande y el \(p_1\) más pequeño tales que \[ \displaystyle\sum_{k=x}^n \left(\begin{array}{c} n \\ k\end{array}\right) \cdot p_0^k\cdot (1-p_0)^{n-k}\leq \frac{\alpha}{2},\quad \displaystyle\sum_{k=0}^x \left(\begin{array}{c} n \\ k\end{array}\right)\cdot p_1^k\cdot(1-p_1)^{n-k}\leq \frac{\alpha}{2} \]

Para hallar un intervalo de confianza para la proporción poblacional en R según el método de Clopper-Pearson, hay que usar la función binom.exact del paquete epitools:

binom.exact(x,n,conf.level)

donde x y n representan, respectivamente, el número de éxitos y el tamaño de la muestra, y conf.level es \(1-\alpha\), el nivel de confianza en tanto por uno.

Ejemplo tabla de datos iris

Hallemos un intervalo de confianza para la proporción de flores con especie “setosa” dada una muestra de 60 flores.

Sabemos que la proporción real \(p\) en este caso vale \(p=\frac{50}{150}=\frac{1}{3}=0.333\).

Primero hallamos la muestra de las 60 flores:

set.seed(1000)
flores.elegidas = sample(1:150,60,replace=TRUE)

Las flores elegidas son: (sólo mostramos las 10 primeras)

muestra.flores.prop = iris[flores.elegidas,]
head(muestra.flores.prop,10)

##     Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
## 68           5.8         2.7          4.1         1.0 versicolor
## 43           4.4         3.2          1.3         0.2     setosa
## 51           7.0         3.2          4.7         1.4 versicolor
## 88           6.3         2.3          4.4         1.3 versicolor
## 29           5.2         3.4          1.4         0.2     setosa
## 99           5.1         2.5          3.0         1.1 versicolor
## 61           5.0         2.0          3.5         1.0 versicolor
## 146          6.7         3.0          5.2         2.3  virginica
## 150          5.9         3.0          5.1         1.8  virginica
## 102          5.8         2.7          5.1         1.9  virginica

El número de flores de especie setosa será:

número.flores.setosa=
  table(muestra.flores.prop$Species=="setosa")[2]
número.flores.setosa

## TRUE 
##   21

El intervalo de confianza para la proproción poblacional de flores de especie setosa al 95% de confianza será:

library(epitools)
binom.exact(número.flores.setosa,60,conf.level=0.95)

##       x  n proportion      lower      upper conf.level
## TRUE 21 60       0.35 0.23132642 0.48402801       0.95

Según el método de Clopper-Pearson, con un 95% de confianza podemos decir que en la tabla de datos iris hay entre un 23.13% y 48.4% de flores de especie “setosa”.

3.2.2 Caso del tamaño \(n\) de la muestra grande

Consideremos la situación siguiente :

• \(X\) una v.a. Bernoulli con \(p\) desconocida.

• \(X_1,\ldots,X_n\) una m.a.s. de \(X\), con \(n\) grande (por Ejemplo, \(n\geq 40\)) y frecuencia relativa de éxitos \(\widehat{p}_{X}\).

En estas condiciones (por el Teorema Central del Límite), \[ Z=\dfrac{\widehat{p}_{X}-p} {\sqrt{\frac{p(1-p)}{n}}}\approx N(0,1) \]

Por lo tanto

\[ P\left(-z_{1-\frac{\alpha}{2}}\leq \dfrac{\widehat{p}_{X}-p} {\sqrt{\frac{p(1-p)}{n}}}\leq z_{1-\frac{\alpha}{2}}\right)=1-\alpha. \]

El problema es que no conocemos \(p\)…

La literatura plantea entre otras soluciones:

• El método de Wilson
• La solución de Laplace (1812)

3.2.3 Método de Wilson

Definición. En estas condiciones, un intervalo de confianza del \((1-\alpha)\cdot 100\%\) I.C. para \(p\) (donde \(\widehat{q}_{X}=1-\widehat{p}_{X}\)) es:

\[ \left(\frac{\widehat{p}_{X}+\frac{z_{1-{\alpha}/{2}}^2}{2n}-z_{1-{\alpha}/{2}}\sqrt{\frac{\widehat{p}_{X}\widehat{q}_{X}}{n}+\frac{z_{1-{\alpha}/{2}}^2}{4n^2}}}{1+\frac{z_{1-{\alpha}/{2}}^2}{n}}\right., \left.\frac{\widehat{p}_{X}+\frac{z_{1-{\alpha}/{2}}^2}{2n}+z_{1-{\alpha}/{2}}\sqrt{\frac{\widehat{p}_{X}\widehat{q}_{X}}{n}+\frac{z_{1-{\alpha}/{2}}^2}{4n^2}}}{1+\frac{z_{1-{\alpha}/{2}}^2}{n}}\right). \]

Para hallar un intervalo de confianza para la proporción poblacional en R según el método de Wilson, hay que usar la función binom.wilson del mismo paquete epitools:

binom.wilson(x,n,conf.level)

Ejemplo tabla de datos iris

Usando el ejemplo anterior, hallemos un intervalo de confianza para la proporción de flores de especie “setosa” según el método de Wilson al 95% de confianza.

El intervalo será:

binom.wilson(número.flores.setosa,60,conf.level=0.95)

##       x  n proportion      lower      upper conf.level
## TRUE 21 60       0.35 0.24167774 0.47637381       0.95

Según el método de Wilson, con un 95% de confianza podemos decir que en la tabla de datos iris hay entre un 24.17% y 47.64% de flores de especie “setosa”.

3.2.4 Fórmula de Laplace.

Supongamos que la muestra aleatoria simple es considerablemente más grande que la usada en el método de Wilson y que, además, la proporción muestral de éxitos \(\widehat{p}_{X}\) está alejada de 0 y de 1.

• O sea, \(n\geq 100\) y que \(n\widehat{p}_{X}\geq 10\) y \(n(1-\widehat{p}_{X})\geq 10\).

• En este caso, podemos usar la fórmula de Laplace: \[ \widehat{p}_{X}\pm z_{1-\alpha/2}\sqrt{\frac{\widehat{p}_{X} (1-\widehat{p}_{X})}{n}}. \]

Para hallar un intervalo de confianza para la proporción poblacional en R según la fórmula de Laplace, hay que usar la función binom.approx del mismo paquete epitools:

binom.approx(x,n,conf.level)

Ejemplo

En una muestra aleatoria de 500 familias con niños en edad escolar se encontró que 340 introducían fruta de forma diaria en la dieta de sus hijos

Calculad un intervalo de confianza del 95% para conocida la proporción real de familias de esta ciudad con niños en edad escolar que incorporen fruta fresca de forma diaria en la dieta de sus hijos.

El tamaño de la muestra es \(n=500\) y la estimación de la proporción muestral, \(\widehat{p}_{X}=\dfrac{340}{500}=0.68\).

Como que \(n=500\geq 100\), \(n\widehat{p}_X=340\geq 10\) y \(n\cdot (1-\widehat{p}_X)=160\geq 10\), podemos utilizar la fórmula de Laplace.

Usando que \(z_{1-\frac{\alpha}{2}}=z_{0.975}=1.96\), el intervalo de confianza será:

\[ \begin{array}{ll} \left(0.68-1.96\cdot \sqrt{\frac{0.68\cdot 0.32}{500}},0.68+1.96\cdot \sqrt{\frac{0.68\cdot 0.32}{500}}\right)& \\ =(0.639, 0.721). & \end{array} \]

Ejemplo tabla de datos iris

Usando el ejemplo anterior, hallemos un intervalo de confianza para la proporción de flores de especie “setosa” según la fórmula de Laplace al 95% de confianza.

El intervalo será:

binom.approx(número.flores.setosa,60,conf.level=0.95)

##       x  n proportion      lower      upper conf.level
## TRUE 21 60       0.35 0.22931226 0.47068774       0.95

Según la fórmula de Laplace, con un 95% de confianza podemos decir que en la tabla de datos iris hay entre un 22.93% y 47.07% de flores de especie “setosa”.

Amplitud del intervalo de confianza.

Problema: hallar el tamaño de la muestra fijada la amplitud del intervalo de confianza.

La amplitud del intervalo de confianza usando la fórmulade Laplace es \[ A=2 z_{1-\frac{\alpha}{2}} \sqrt{\frac{\widehat{p}_{X} (1-\widehat{p}_{X})}{n}}. \]

No podemos determinar el tamaño de la muestra para que el intervalo de confianza tenga como máximo una cierta amplitud sin conocer \(\widehat{p}_{X}\).

Vamos a considerar que estamos en el peor de los casos.

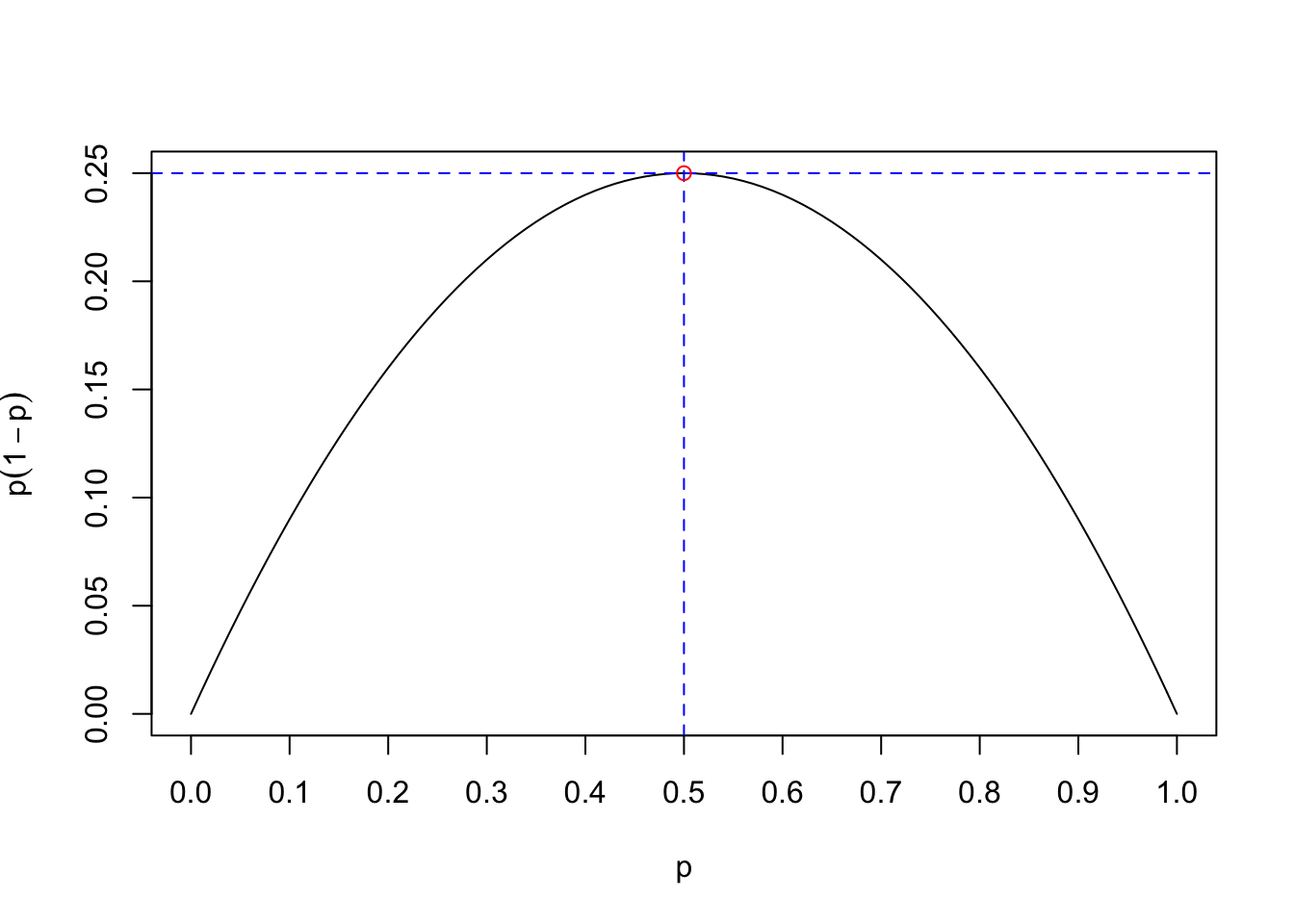
O sea, usando que \(\widehat{p}_{X}\in [0,1]\), nos planteamos hallar el máximo de la expresión \(\widehat{p}_{X} (1-\widehat{p}_{X})\) que aparece en la fórmula de la amplitud.

El máximo de la función anterior, para \(\widehat{p}_{X}\in [0,1]\) se alcanza en \(\widehat{p}_{X}=\frac{1}{2}\) y dicho máximo vale \(\frac{1}{4}\):

Ejercicio

Demostrar que el máximo de la función \(f(p) = p(1-p)\) se alcanza en \(p=1/2\) y vale \(1/4\).

En resumen, calcularemos \(n\) para obtener una amplitud máxima \(A_0\) suponiendo el peor de los casos (\(\widehat{p}_{X}=0.5\)): \[ A_0\geq 2z_{1-\frac{\alpha}{2}}\sqrt{\frac{0.5^2}{n}}=\frac{z_{1-\frac{\alpha}{2}}}{\sqrt{n}} \Rightarrow n\geq \left\lceil\frac{z_{1-\frac{\alpha}{2}}^2}{A_0^2}\right\rceil. \]

Ejemplo de los teléfonos móviles

Quemos estudiar qué fración teléfonos móviles utilizan android para determinar esta proporción con un nivel de confianza del 95% y garantizar un error máximo de 0.05.

¿De qué tamaño ha de ser la muestra en el peor de los casos?

Usando la fórmula anterior, el valor de \(n\) tiene que verificar: \[ n\geq \left\lceil\frac{z_{1-\frac{\alpha}{2}}^2}{A^2}\right\rceil \] donde \(\frac{A}{2}=0.05\), (\(A=0.1\)) y \(z_{1-\frac{\alpha}{2}}=z_{0.975}=1.96\).

El tamaño de la muestra valdrá, como mínimo: \[ n\geq \left\lceil\frac{1.96^2}{0.1^2}\right\rceil =\lceil384.146 \rceil=385. \]

3.3 Intervalo de confianza para la varianza de una población normal

Consideremos la siguiente situación:

• Consideramos una \(X\) una v.a. normal con \(\mu\) y \(\sigma\) desconocidas.

• Sea \(X_1,\ldots,X_n\) una m.a.s. de \(X\) y varianza muestral \(\widetilde{S}_X^2\).

En estas condiciones tenemos el siguiente:

Teorema.

La variable aleatoria \(\frac{(n-1) \tilde{S}_{X}^2}{\sigma^2}\) se distribuye según una distribución \(\chi^2_{n-1}\).

Teorema.

En las condiciones anteriores, un intervalo de confianza del \((1-\alpha)\cdot 100\%\) para la varianza \(\sigma^2\) de la población \(X\) es \[ \left( \frac{(n-1)\widetilde{S}_{X}^2}{\chi_{n-1,1-\frac{\alpha}{2}}^2}, \frac{(n-1)\widetilde{S}_{X}^2}{\chi_{n-1,\frac{\alpha}{2}}^2} \right), \] donde \(\chi_{\nu,q}^2\) es el \(q\)-cuantil de la distribución \(\chi_{\nu}^2\).

Ejemplo

Un algoritmo probabilístico depende de la semilla de aleatorización que se genera en cada paso. Para saber si la semilla influye mucho en el resultado se ejecuta el algoritmo varias veces hasta obtener un resultado similar y se estudia la varianza de su tiempo de ejecución.

Queremos ver si la desviación típica \(\sigma\) es \(\leq 30\).

Se supone que la distribución del tiempo de ejecución del algoritmo es aproximadamente normal.

Se realizan 30 ejecuciones del algoritmo de las que se mide el tiempo de ejecución. Los resultados son:

tiempo=c(12, 13, 13, 14, 14, 14, 15, 15, 16, 17,
         17, 18, 18, 19, 19, 25, 25, 26, 27, 30,
         33, 34, 35, 40, 40, 51, 51, 58, 59, 83)

Nos piden calcular un intervalo de confianza para \(\sigma^2\) del tiempo de ejecución a un \(95\%\) de confianza.

En primer lugar calculamos la varianza muestral de nuestra muestra:

n=30
(var.muestral.tiempo = var(tiempo))

## [1] 301.55057

En segundo lugar, calculamos los cuantiles que necesitamos:

alpha=0.05
(cuantil.izquierda = qchisq(1-alpha/2,n-1))

## [1] 45.722286

(cuantil.derecha = qchisq(alpha/2,n-1))

## [1] 16.047072

El intervalo de confianza para la varianza del tiempo de ejecución será:

(valor.izquierdo= (n-1)*var.muestral.tiempo/cuantil.izquierda)

## [1] 191.26267

(valor.derecho= (n-1)*var.muestral.tiempo/cuantil.derecha)

## [1] 544.95716

El intervalo de confianza para la desviación típica \(\sigma\) del tiempo de ejecución será:

c(sqrt(valor.izquierdo),sqrt(valor.derecho))

## [1] 13.829775 23.344318

Vemos que el valor 30 está a la derecha del intervalo de confianza.

Por tanto, podemos afirmar con un 95% de confianza que \(\sigma\leq 30\).

3.3.1 Intervalo de confianza para la varianza de una población normal en R

Para hallar un intervalo de confianza para la varianza poblacional en R hay que usar la función varTest del paquete EnvStats:

varTest(X,conf.level)$conf.int

donde X es el vector que contiene la muestra y conf.level el nivel de confianza, que por defecto es igual a 0.95.

Ejemplo

Hallemos un intervalo de confianza para la varianza de la amplitud del sépalo de la tabla de datos iris a partir de la muestra anterior. Suponemos que dicha variable es normal. Veremos en temas posteriores cómo se puede comprobar la normalidad de una variable.

Hallemos los valores de la amplitud del sépalo para las flores de nuestra muestra:

(amplitud.sépalo.muestra = iris[flores.elegidas,]$Sepal.Width)

##  [1] 2.7 3.2 3.2 2.3 3.4 2.5 2.0 3.0 3.0 2.7 3.8 3.4 2.7 3.5 3.5 3.0 2.3 3.2 2.0
## [20] 2.8 2.5 2.3 3.1 3.0 2.3 2.9 3.4 3.1 3.4 2.5 2.6 3.7 2.5 4.4 3.0 3.4 2.5 2.5
## [39] 3.2 3.0 3.3 3.2 3.8 3.6 3.0 3.4 2.8 2.6 2.9 3.1 3.1 3.3 3.2 3.2 3.5 3.5 3.0
## [58] 3.4 3.1 2.3

Un intervalo de confianza para la varianza de las amplitudes del sépalo para la tabla de datos iris al 95% de confianza será:

library(EnvStats)
varTest(amplitud.sépalo.muestra,conf.level=0.95)$conf.int

##        LCL        UCL 
## 0.16256399 0.33657861 
## attr(,"conf.level")
## [1] 0.95

3.4 Bootstrap o remuestreo

Cuando no se satisfacen las condiciones teóricas que garantizan que el intervalo obtenido contiene el 95% de las veces el parámetro poblacional deseado, podemos recurrir a un método no paramétrico. El más utilizado es el bootstrap, que básicamente consiste en:

1. Remuestrear la muestra: tomar muchas muestras aleatorias simples de la muestra de la que disponemos, cada una de ellas del mismo tamaño que la muestra original (pero simples, es decir, con reposición).

2. Calcular el estimador sobre cada una de estas submuestras.

3. Organizar los resultados en un vector.

4. Usar este vector para calcular un intervalo de confianza.

3.4.1 Bootstrap: método de los percentiles

La manera más sencilla de llevar a cabo el cálculo final del intervalo de confianza es el llamado método de los percentiles , en el que se toman como extremos del intervalo de confianza del \((1-\alpha)\cdot 100\%\) los cuantiles de orden \(\frac{\alpha}{2}\) y \(1-\frac{\alpha}{2}\) del vector de estimadores.

Ejemplo

Como aplicación del método de los percentiles hallemos un intervalo de confianza para la varianza de la longitud del pétalo de la tabla de datos iris.

No podemos usar la fórmula vista anteriormente ya que la variable considerada no puede considerarse normal.

Tomaremos la muestra de la tabla de datos iris que hemos calculado anteriormente en la sección de intervalo de confianza para proporciones.

Usaremos la función replicate de R para calcular las varianzas de 1000 muestras “remuestradas” de nuestra muestra original:

set.seed(42)
X=replicate(1000, 
            var(sample(iris[flores.elegidas,]$Petal.Length,
                       replace=TRUE)
                )
            )

A continuación hallamos el intervalo de confianza al 95% (\(1-\alpha=0.95\)) calculando los cuantiles del método: (cuantiles de orden \(\frac{\alpha}{2}=0.025\) y \(1-\frac{\alpha}{2}=0.975\))

alpha = 0.05
IC.boot=c(quantile(X,alpha/2),quantile(X,1-alpha/2))
round(IC.boot,2)

##  2.5% 97.5% 
##  2.41  3.53

Para aplicar el método de los percentiles en R, podemos usar la función boot del paquete boot:

boot(X,estadístico,R)

donde:

• X es el vector que forma la muestra de la que disponemos

• R es el número de muestras que queremos extraer de la muestra original

• El estadístico es la función que calcula el estadístico deseado de la submuestra, y tiene que tener dos parámetros: el primero representa la muestra original X y el segundo representa el vector de índices de una m.a.s. de X.

Ejemplo anterior

Vamos a aplicar la función boot al ejemplo anterior definiendo primero el estadístico a usar que sería la varianza en nuestro caso.

library(boot)

## 
## Attaching package: 'boot'

## The following objects are masked from 'package:faraway':
## 
##     logit, melanoma

var.boot=function(X,índices){var(X[índices])}
simulación=boot(iris[flores.elegidas,]$Petal.Length,var.boot,1000)

El intervalo de confianza viene dado por la función boot.ci:

boot.ci(simulación)

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = simulación)
## 
## Intervals : 
## Level      Normal              Basic         
## 95%   ( 2.531,  3.567 )   ( 2.529,  3.603 )  
## 
## Level     Percentile            BCa          
## 95%   ( 2.409,  3.483 )   ( 2.488,  3.535 )  
## Calculations and Intervals on Original Scale

Obtenemos cuatro intervalos de confianza para \(\sigma^2\), calculados con cuatro métodos a partir de la simulación realizada.

El intervalo Percentile es el calculado con el método de los percentiles que hemos explicado antes, y se obtiene con el sufijo $percent[4:5].

Vemos que los valores son parecidos a los obtenidos en la simulación hecha a mano.

Ejercicio

Mirando la documentación e investigando un poco, elaborad un pequeño resumen de cómo se obtienen y qué significan cada uno de los otros tres intervalos de confianza de la función boot.ci.

3.5 Guía rápida

• t.test(X, conf.level=...)$conf.int calcula el intervalo de confianza del conf.level\(\times 100\%\) para la media poblacional usando la fórmula basada en la t de Student aplicada a la muestra X.

• binom.exact(x,n,conf.level=...) del paquete epitools, calcula el intervalo de confianza del conf.level\(\times 100\%\) para la proporción poblacional aplicando el método de Clopper-Pearson a una muestra de tamaño n con x éxitos.

• binom.wilson(x,n,conf.level=...) del paquete epitools, calcula el intervalo de confianza del conf.level\(\times 100\%\) para la proporción poblacional aplicando el método de Wilson a una muestra de tamaño n con x éxitos.

• binom.approx(x,n,conf.level=...) del paquete epitools, calcula el intervalo de confianza del conf.level\(\times 100\%\) para la proporción poblacional aplicando la fórmula de Laplace a una muestra de tamaño n con x éxitos.

• varTest(X,conf.level=...)$conf.int del paquete EnvStats, calcula el intervalo de confianza del conf.level\(\times 100\%\) para la varianza poblacional usando la fórmula basada en la khi cuadrado aplicada a la muestra X.

• boot(X,E,R) del paquete boot, lleva a cabo una simulación bootstrap, tomando R submuestras del vector X y calculando sobre ellas el estadístico representado por la función E.

• boot.ci del paquete boot, aplicado al resultado de una función boot, calcula diversos intervalos de confianza a partir del resultado de la simulación efectuada con boot. El nivel de confianza se especifica con el parámetro conf.