Tema 9 Introducción al Clustering

Uno de los problemas que más se presentan en el ámbito del machine learning es la clasificación de objetos.

Más concretamente, nos planteamos el problema siguiente: dado un conjunto de objetos, clasificarlos en grupos (clusters) basándonos en sus parecidos y diferencias.

9.1 ¿Qué es el clustering?

Algunas aplicaciones del clustering son las siguientes:

En Biología: clasificación jerárquica de organismos (relacionada con una filogenia), agrupamiento de genes y agrupamiento de proteínas por parecido estructural.
En Marketing: identificación de individuos por comportamientos similares (de compras, ocio, etc.)
En Tratamiento de imágenes (en particular imágenes médicas): eliminación de ruido, detección de bordes, etc.
En Biometría: identificación de individuos a partir de sus caras, huellas dactilares, etc.

9.1.1 Principios básicos

Los algoritmos de clasificación o clustering deben verificar dos principios básicos:

Homogeneidad: los clusters deben ser homogéneos en el sentido de que objetos dentro de un mismo cluster tienen que ser próximos o parecidos.
Separación: los objectos que pertenezcan a clusters diferentes tienen que estar alejados.

En los dos gráficos de la figura siguiente vemos un ejemplo de dos algoritmos de clustering donde en el de la izquierda, los clusters cumplen los principios anteriores pero en el de la derecha se violan los dos principios.

9.1.2 Tipos de algoritmos de clustering

Vamos a intentar formalizar los principios anteriores de cara a definir algoritmos de clustering que los verifiquen.

Existen dos tipos de algoritmos de clustering:

De partición: el número de clusters con los que vamos a clasificar nuestro conjunto de objetos es un valor conocido y prefijado de entrada.

Sin embargo, veremos métodos que nos dirán como calcular el número óptimo de cantidad de clusters con los que dividir o clasificar nuestros objectos de nuestra tabla de datos. Por ejemplo, si consideramos los objetos de la figura anterior, se observa gráficamente que el número óptimo de clusters con los que clasificar dichos puntos es 2.

Jerárquico: el algoritmo de clustering se compone de un número finito de pasos donde usualmente dicho número coincide con el número de objetos menos uno.

Los métodos jerárquicos a su vez se subclasifican en dos tipos más:

métodos aglomerativos, donde en el paso inicial todos los objetos están separados y forman un cluster de un sólo objeto y en cada paso, se van agrupando aquellos objetos o clusters más próximos hasta llegar a un único cluster formado por todos los objetos.
métodos divisivos, donde en el paso inicial existe un único cluster formado por todos los objetos y en cada paso se van dividiendo aquellos clusters más heterogéneos hasta llegar a tantos clusters como objetos existían inicialmente.

Los métodos jerárquicos tanto aglomerativos como divisivos producen un árbol binario de clasificación donde cada nodo de dicho árbol indica una agrupación de un cluster en dos en el caso de los métodos aglomerativos y una partición de un cluster en dos en el caso de los métodos divisivos.

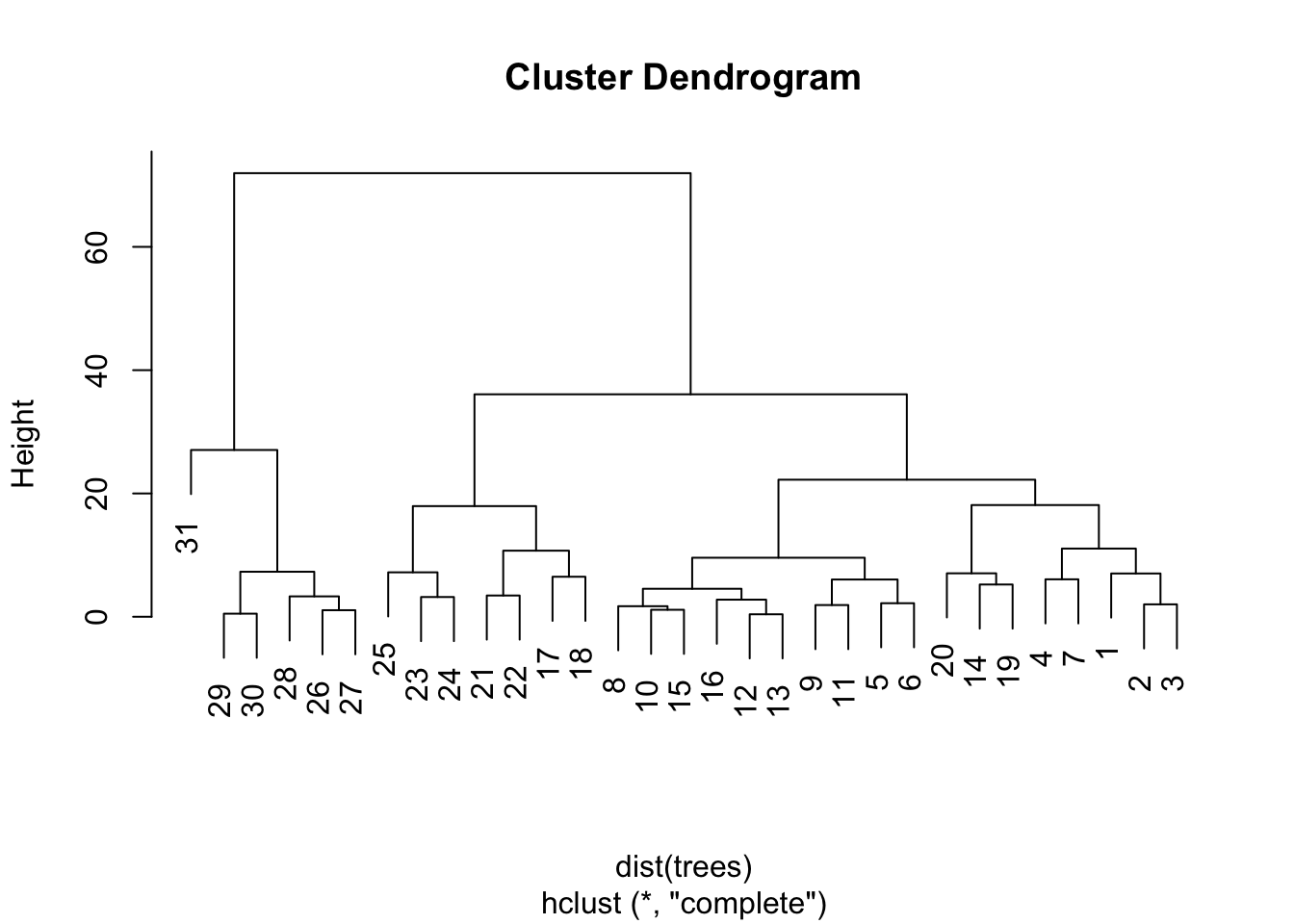
En el siguiente gráfico, se observa cómo se han clasificado los 31 árboles de la tabla de datos trees de R a partir de los valores de las tres variables de dicha tabla de datos usando un método jerárquico aglomerativo:

Girth: el valor del contorno del diámetro del árbol en pulgadas.
Height: la altura del árbol en pies.
Volume: el volumen del tronco del árbol en pies cúbicos.

Fijaos cómo al principio en la base del árbol todos los árboles forman un cluster y en la cima del árbol hay un único cluster formado por todos los árboles.

9.2 Métodos de partición

9.2.1 Algoritmo de las $k$-medias ($k$-means)

El algoritmos de las $k$-medias o $k$-means en inglés es el algoritmo de partición más conocido y más usado.

Recordemos que, al ser un algoritmo de partición, el número de clusters $k$ se ha prefijado de entrada.

Dicho algoritmo busca una partición del conjunto de objetos, donde suponemos que conocemos un conjunto de características o variables que tienen valores continuos.

Concretamente, tenemos una tabla de datos de $n$ filas y $m$ columnas, donde cada fila representa un objeto u individuo y cada columna representa una característica de dicho individuo.

Individuos/Variables	$X_1$	$X_2$	$\ldots$	$X_m$
1	$x_{11}$	$x_{12}$	$\ldots$	$x_{1m}$
2	$x_{21}$	$x_{22}$	$\ldots$	$x_{2m}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$i$	$x_{i1}$	$x_{i2}$	$\ldots$	$x_{im}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$n$	$x_{n1}$	$x_{n2}$	$\ldots$	$x_{nm}$

Por tanto, podemos identificar el individuo $i$-ésimo con un vector $\mathbf{x}_i =(x_{i1},x_{i2},\ldots,x_{im})$ de $\mathbb{R}^m$.

El algoritmo de las $k$-medias va a clasificar los $n$ individuos usando la información de la tabla anterior, es decir, la información de las $m$ variables continuas.

Para realizar dicha clasificación, necesitamos definir cuándo dos objetos están próximos.

Una manera de definir la proximidad entre dos individuos, (no es la única) es a partir de la distancia euclídea.

Dados dos objetos $\mathbf{x}$ y $\mathbf{y}$ en $\mathbb{R}^m$, se define la distancia euclídea entre los dos como: \[ \|\mathbf{x}-\mathbf{y}\|=\sqrt{\sum_{i=1}^m (x_i-y_i)^2}. \] Para $m=2$ o $m=3$, la distancia euclídea es la longitud del segmento que une los puntos $\mathbf{x}$ e $\mathbf{y}$.

Por tanto, dos objectos estarán más próximos, cuánto más pequeña sea la distancia euclídea entre ambos.

Una vez establecidos las bases para el algoritmo, enunciemos el objetivo del mismo:

El objetivo del algoritmo de las $k$-medias es, a partir de la tabla de datos anterior de $n$ filas (los individuos u objetos) y $m$ columnas (las variables), hallar $k$ puntos $\mathbf{c}_1,\ldots,\mathbf{c}_k\in \mathbb{R}^n$ que minimicen \[ SS_C(\mathbf{x}_1,\ldots,\mathbf{x}_n; k)=\sum_{i=1}^n\min_{j=1,\ldots,k} \|\mathbf{x}_i-\mathbf{c}_j\|^2. \] La cantidad $SS_C$ se denomina suma de cuadrados dentro de los clusters.

Estos $k$ puntos $\mathbf{c}_1,\ldots,\mathbf{c}_k$ serán los centros de los clusters $C_1,\ldots,C_k$ que queremos hallar.

Fijaos que, una vez hallados dichos centros $\mathbf{c}_1,\ldots,\mathbf{c}_k$, los clusters quedan definidos por: \[ C_j=\{\mathbf{x}_i\mbox{ tal que} \|\mathbf{x}_i-\mathbf{c}_j\|<\|\mathbf{x}_i-\mathbf{c}_l\|\mbox{ para todo }l\neq j\} \] Es decir, el cluster $i$-ésimo estará formado por los objetos $\mathbf{x}_l$ más próximos al centro $\mathbf{c}_i$.

Desgraciadamente, el problema anterior es un problema abierto, es decir, no se sabe hallar la solución para cualquier tabla de datos.

El algoritmo de las $k$-medias es un intento de hallar una solución local del mismo. Es decir, halla unos centros $\mathbf{c}_1,\ldots,\mathbf{c}_k$ que solucionan el problema parcialmente pero no tenemos asegurado que los centros que halla el algoritmo minimicen globalmente $SS_C$.

Una vez establecidos las bases y el objetivo del algoritmo, vamos a explicar los pasos de los que consta.

Existen bastantes variantes del algoritmo de las $k$-medias, básicamente se diferencian en cómo iniciamos el algoritmo. En este curso, explicaremos el algoritmo de Lloyd:

Paso 1: escogemos aleatoriamente los centros $\mathbf{c}_1,\ldots,\mathbf{c}_k$.
Paso 2: para cada $i=1,\ldots,n$, asignamos el individuo $i$-ésimo, $\mathbf{x}_i$, al cluster $C_j$ definido por el centro $\mathbf{c}_j$ más próximo. Dicho en otras palabras, definimos los clusters a partir de los centros como hemos explicado antes.
Paso 3: una vez hallados los clusters, hallamos los nuevos centros $\mathbf{c}_j$ calculando el valor medio de los objetos que forman el cluster $C_j$: \[ \mathbf{c}_j= \Big(\sum_{\mathbf{x}_i\in C_j} \mathbf{x}_i\Big)/|C_j|. \]
Paso 4: se repiten los pasos 2 y 3 hasta que los clusters estabilizan, o se llega a un número prefijado de iteraciones ya que el algoritmo anterior puede entrar en un “bucle infinito”.

Observación: el resultado final, es decir, los clusters obtenidos, depende de cómo inicializemos el algoritmo, es decir, de cómo definamos los centros iniciales $\mathbf{c}_1,\ldots,\mathbf{c}_k$.

Como ya hemos comentado, el algoritmo anterior no tiene porque dar un clustering óptimo, es decir, los centros obtenidos $\mathbf{c}_1,\ldots,\mathbf{c}_k$ no tienen por qué minimizar la suma de cuadrados de los clusters $SS_C$. Por este motivo, conviene repetirlo varias veces con diferentes inicializaciones.

Ejemplo

Veamos un ejemplo de aplicación del algoritmo de $k$-medias.

La figura siguiente nos muestra los valores de un conjunto de puntos en el plano y queremos clasificarlos en 3 clusters usando el algoritmo de $k$-medias.

En la figura se observa el paso 1: una elección inicial de los centros $\mathbf{c}_1,\mathbf{c}_2$ y $\mathbf{c}_3$ representados con tres cuadrados de color verde, azul y rojo.

Por tanto, las dos coordenadas de los puntos serían las variables. Como consecuencia, tendríamos que $m=2$.

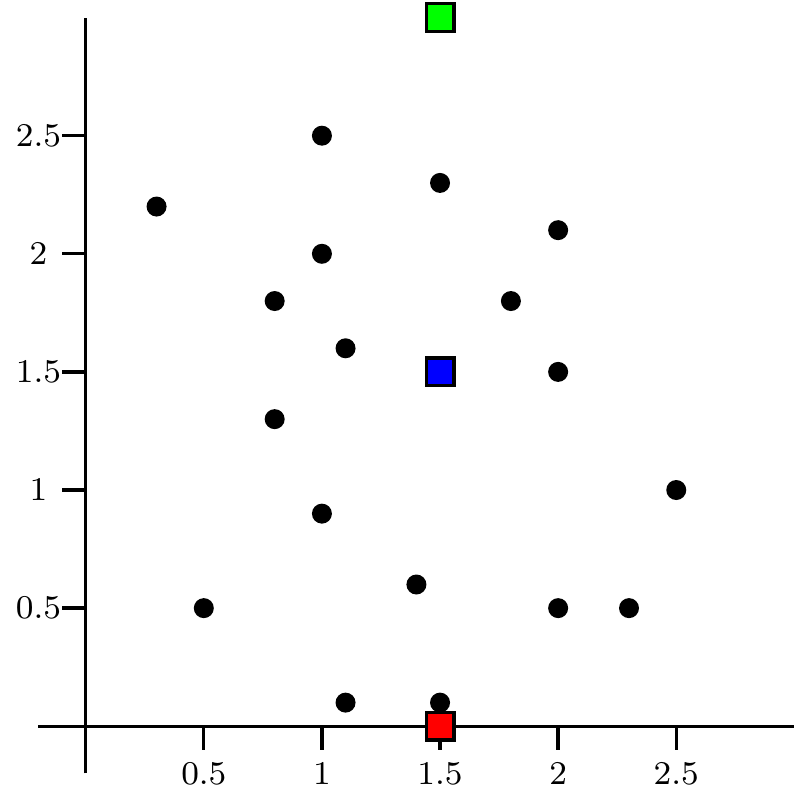
Figure 9.1: Configuración inicial o paso 1

En la figura siguiente, observamos el paso 2 del algoritmo, es decir, la creación de los clusters correspondientes a los tres centros iniciales.

Los puntos de color verde son los puntos más cercanos al centro de color verde, los puntos de color azul son los puntos más cercanos al centro de color azul y los puntos de color rojo son los puntos más cercanos al centro de color rojo.

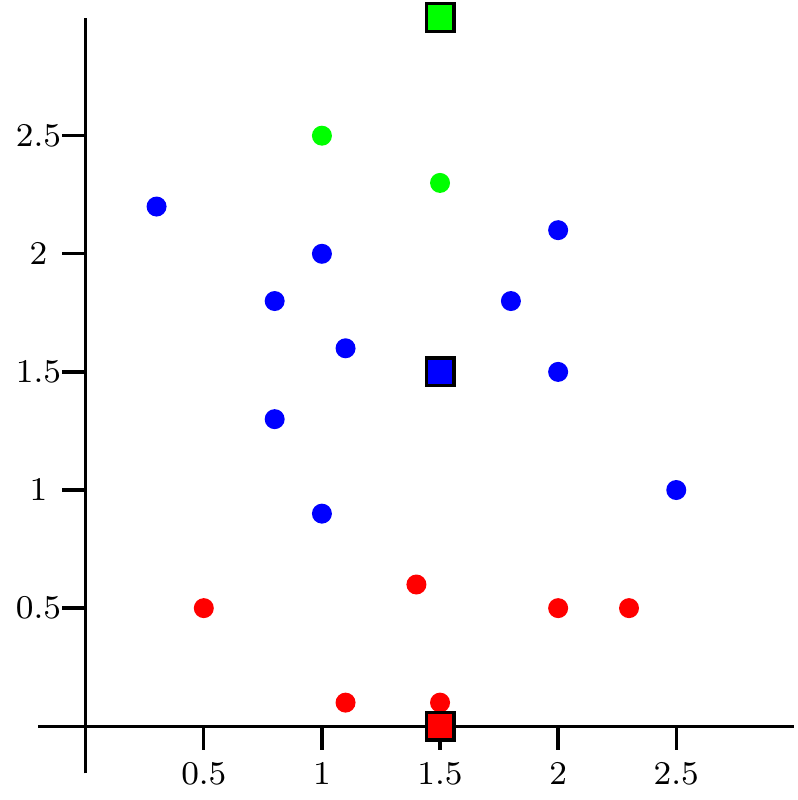
Figure 9.2: Paso 2

En el tercer paso de aplicación del algoritmo, recalculamos los centros a partir del valor medios de los puntos que forman cada cluster $C_j$, $j=1,2,3$ en la siguiente figura.

Por ejemplo, el centro de los dos puntos que forman el cluster de color verde está situado en medio de dichos puntos.

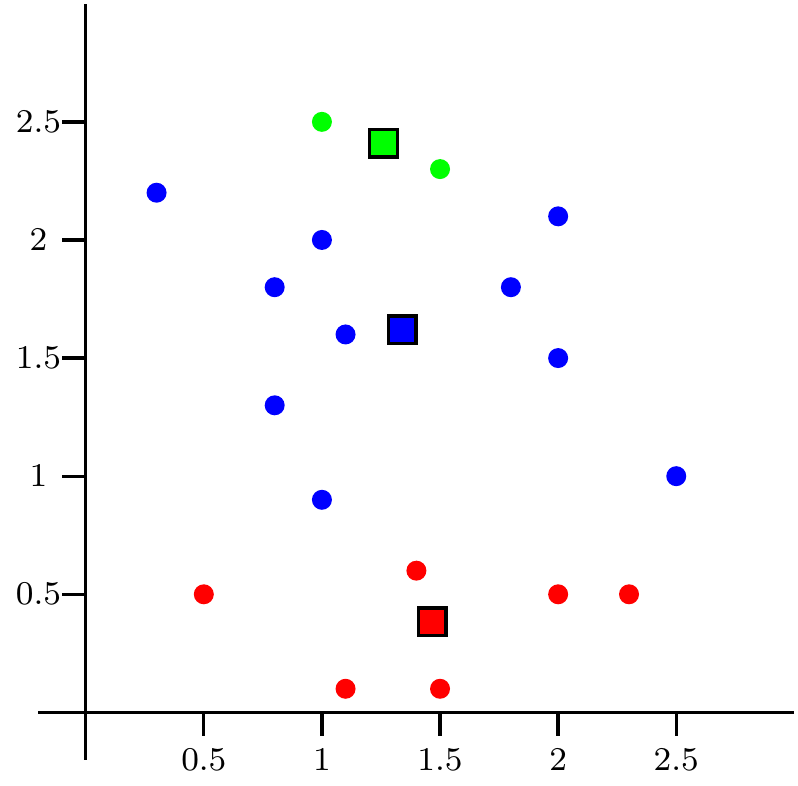
Figure 9.3: Paso 3

En el paso 4 repetimos los pasos 2 y 3 hasta que el algoritmo se estabiliza.

En la figuras siguientes repetimos los pasos 2 y 3.

Recordemos que en los pasos 2, recalculamos los clusters para los nuevos centros recalculados, es decir, asignamos a cada punto al cluster cuyo centro sea más cercano a dicho punto.

En los pasos 3, calculamos los nuevos centros para los clusters calculados en el paso 2.

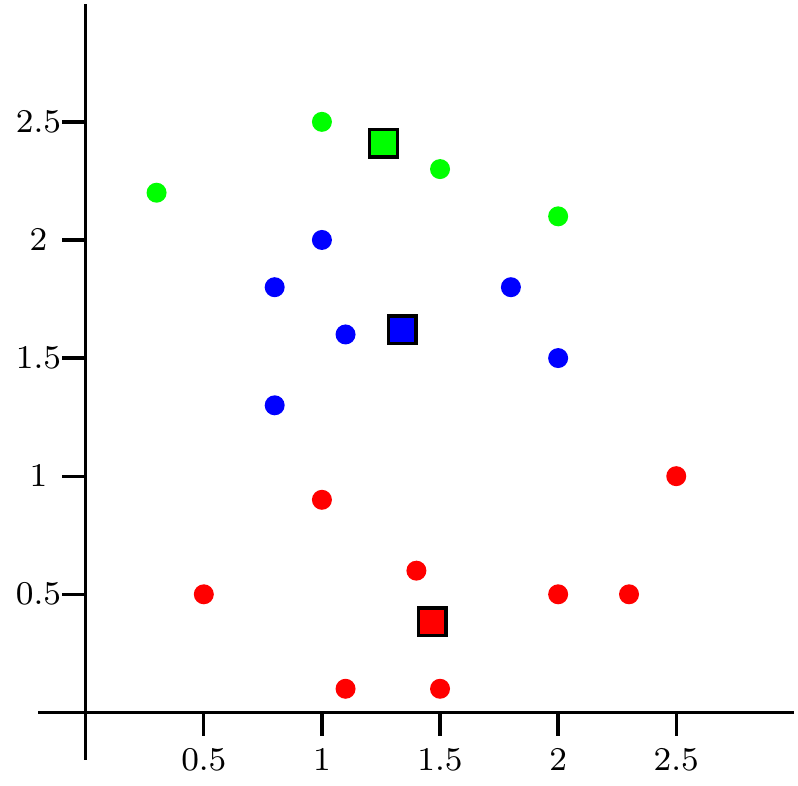
Figure 9.4: Paso 4: repetimos paso 2

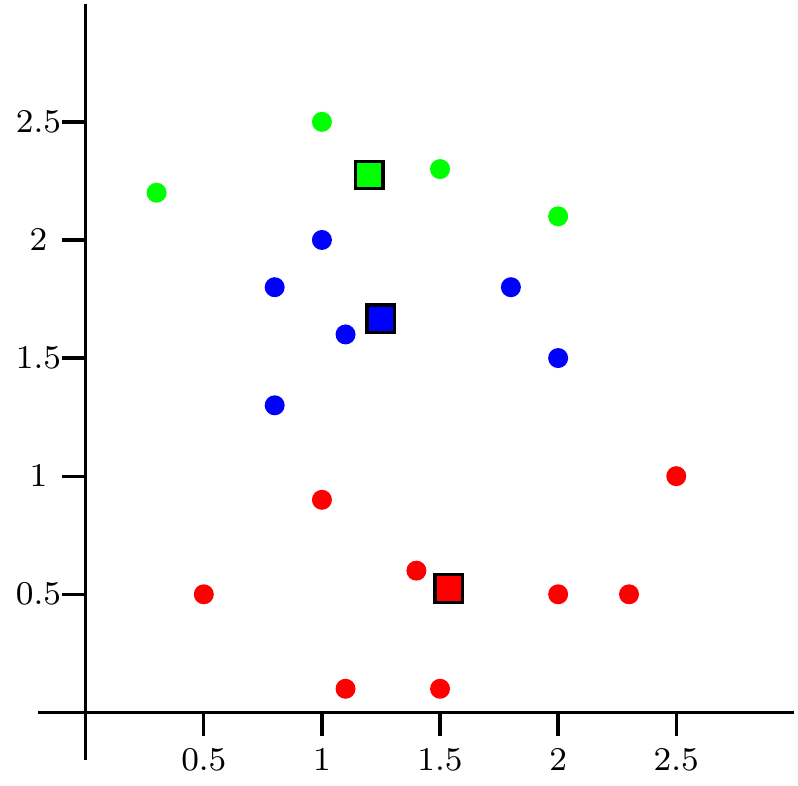
Figure 9.5: Repetimos paso 3

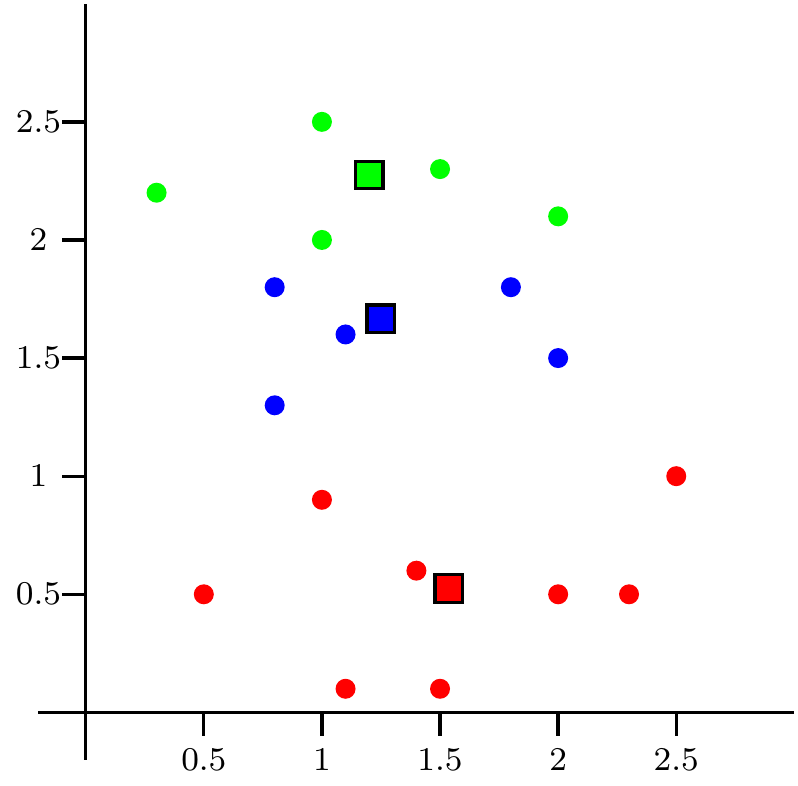
Figure 9.6: Repetimos paso 2

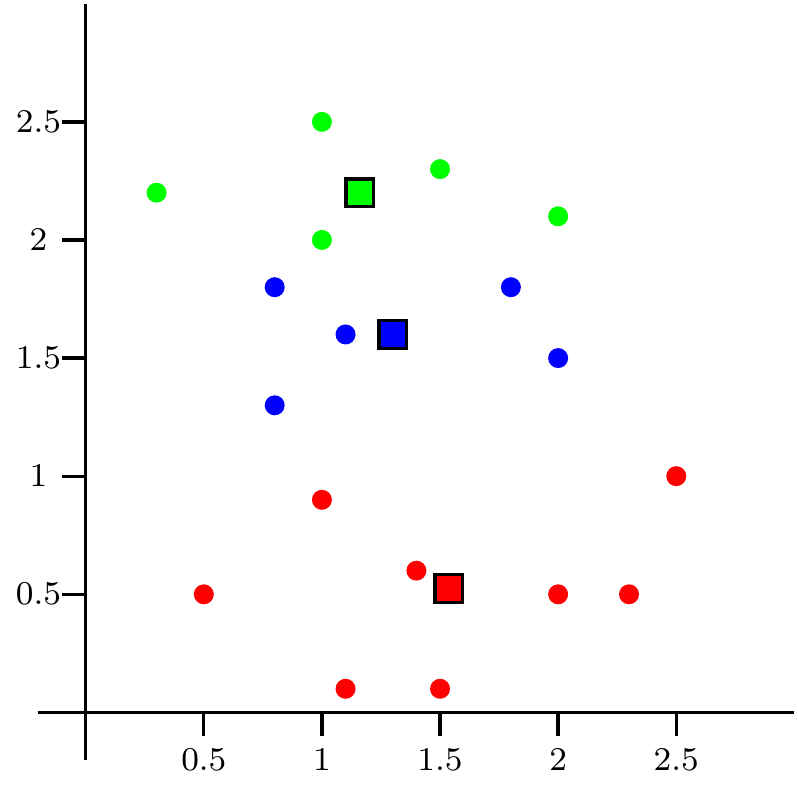
Figure 9.7: Repetimos paso 3

En la última figura el algoritmo se ha estabilizado con un valor de la suma de cuadrados de los clusters de $SS_C=7.25375$.

9.2.2 Limitación del algoritmo de $k$-medias

El algoritmo de $k$-medias tiene las limitaciones siguientes:

No existe un método eficiente y universal de elegir los centros de partida.
Como ya hemos comentado anteriormente, no se puede garantizar un óptimo global.
No se puede determinar de manera efectiva el número $k$ de clusters a priori aunque existe algún método como veremos más adelante.
Si no queremos que la variación de los datos intervenga en el análisis, conviene estandarizar dichos datos ya que el algoritmo no es invariante a cambio de escala. De esta manera todas las variables tendrán media 0 y varianza 1.
El algoritmo es sensible a outliers o datos atípicos.
Si nuestra tabla de datos contiene variables no numéricas tipo factor, ordinales, etc., el algoritmo no se puede aplicar. Es decir, sólo es aplicable para variables continuas que tengan valores en $\mathbb{R}^n$ usando la distancia euclídea.
Los clusters que encuentra son esféricos debido a que usa la distancia euclídea.

9.2.3 Métodos para hallar el número de clusters $k$. Método del codo

Vamos a ver el método más usado para determinar el número óptimo de clusters a calcular con el algoritmo de las $k$ medias.

Uno de dichos métodos se denomina el método del codo. Dicho método se basa en observar como varía la suma de cuadrados de los clusters $SS_C$ como función del número de clusters $k$ y escoger aquel valor $k$ que haga que la variación de dicha función sea lo más pronunciada posible.

La idea es que dicho $k$ es el valor óptimo en el sentido que hace que la disminución de $SS_C$ sea lo más “óptima” posible.

Veamos un ejemplo para ver cómo aplicar el método del codo para hallar el número óptimo de clusters $k$.

Ejemplo

Consideremos la tabla de datos trees de R que ya hemos comentado anteriormente.

En la figura siguiente observamos como evoluciona el valor de la suma de cuadrados de los clusters $SS_C$ con el número de clusters $k$:

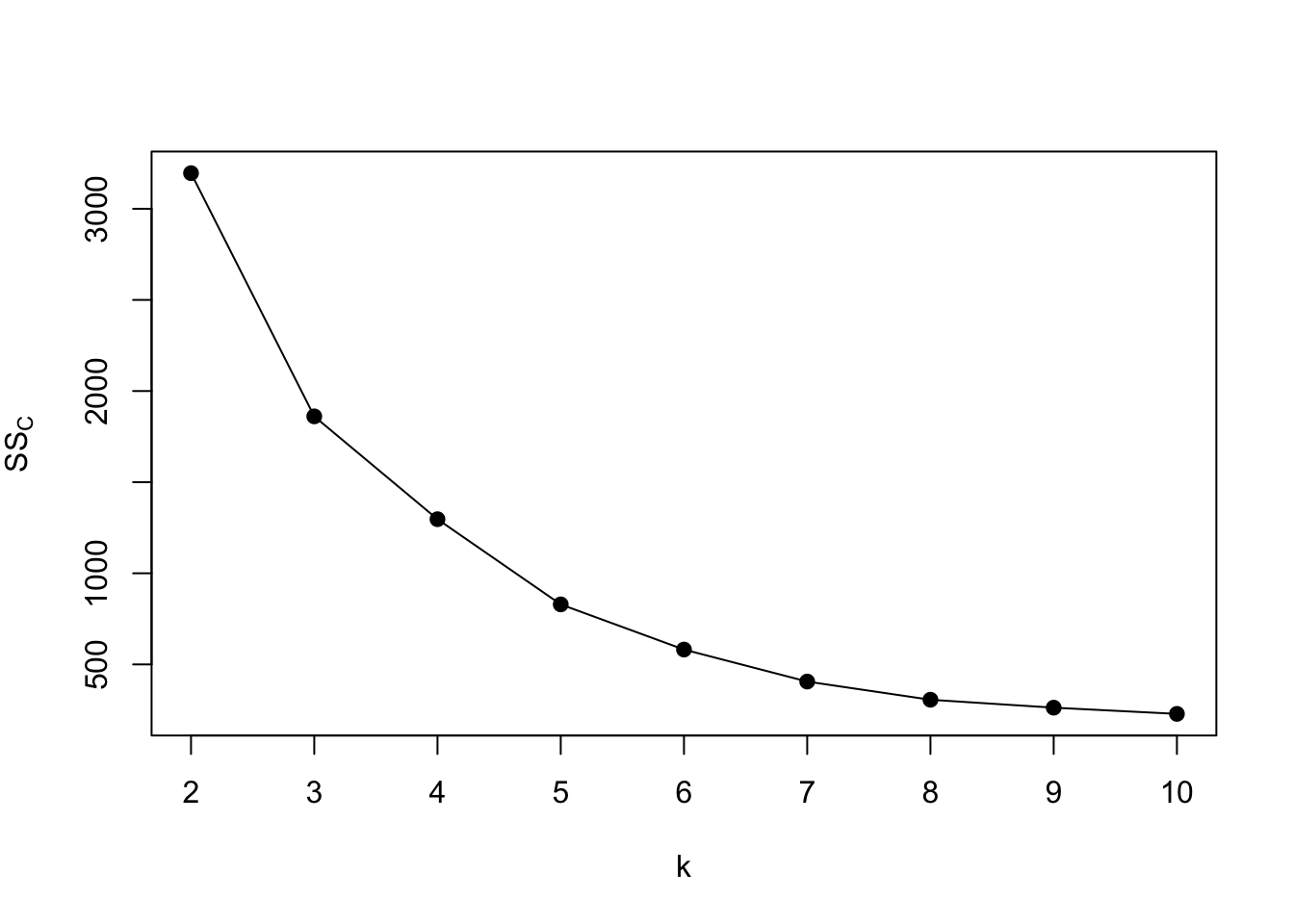
Vemos que la función $SS_C(k)$ es una función cóncava.

El método del codo elige el valor $k$ a partir del cual $SS_C$ disminuye mucho más lentamente que antes de él.

Dicho matemáticamente, el valor $k$ óptimo es aquel en el que la variación de la pendiente antes de $k$ y después de $k$ es más pronunciada.

Los valores de las pendientes en el gráfico anterior son los siguientes:

$k$’s	2-3	3-4	4-5	5-6	6-7	7-8	8-9	9-10
	-1334.531	-564.209	-467.337	-247.838	-175.649	-99.766	-43.484	-34.082

Entonces el $k$ óptimo es $k=3$ en este caso.

9.2.4 Algoritmo de $k$-medias con `R`

Para ejecutar el algoritmo de $k$-medias con R hay que usar la función kmeans:

kmeans(x, centers=..., iter.max=..., algorithm =...)

donde:

x es la matriz o el data frame cuyas filas representan los objetos; en ambos casos, todas las variables han de ser numéricas como ya hemos indicado.
centers sirve para especificar los centros iniciales, y se puede usar de dos maneras: igualado a un número $k$, R escoge aleatoriamente los $k$ centros iniciales, mientras que igualado a una matriz de $k$ filas y el mismo número de columnas que x, R toma las filas de esta matriz como centros de partida.
iter.max permite especificar el número máximo de iteraciones a realizar; su valor por defecto es 10. Al llegar a este número máximo de iteraciones, si el algoritmo aún no ha acabado porque los clusters aún no hayan estabilizado, se para y da como resultado los clusters que se han obtenido en la última iteración.
algorithm indica el algoritmo a usar. Los algoritmos pueden ser los siguientes:
- Lloyd: es el que hemos explicado.
- Hartigan-Wong: este algoritmo empieza igual que el de Lloyd: se escogen $k$ centros, se calculan las distancias euclídeas de cada punto a cada centro, y se asigna a cada centro el cluster de puntos que están más cerca de él que de los otros centros. A continuación, en pasos sucesivos se itera el bucle 1–5 siguiente hasta que en una iteración del mismo los clusters no cambian:
1. Se sustituye cada centro por el punto medio de los puntos asignados a su cluster.
2. Se calculan las distancias euclídeas de cada punto a cada centro.
3. Se asigna (temporalmente) a cada centro el cluster formado por los puntos que están más cerca de él que de los otros centros.
4. Si en esta asignación algún punto ha cambiado de cluster, digamos que el punto $\mathbf{x}_i$ se ha incorporado al cluster $C_j$ de centro $\mathbf{c}_j$, entonces:
- Se calcula el valor $SSE_j$ que se obtiene multiplicando la suma de cuadrados de cada cluster $SS_{C_j}=\sum\limits_{l=1}^{n_j} \|\mathbf{x}_{jl}-\mathbf{c}_j\|^2$, donde $\mathbf{x}_{jl}$ son los puntos del cluster $C_j$, para $l=1,\ldots,n_j$, por $n_j/(n_j−1)$ (donde $n_j$ indica el número de elementos del cluster $C_j$).
- Se calcula, para todo otro cluster $C_k$, el correspondiente valor $SSE_{i,k}$ como si $\mathbf{x}_i$ hubiera ido a parar a $C_k$.
- Si algún $SSE_{i,k}$ resulta menor que $SSE_j$, $\mathbf{x}_i$ se asigna definitivamente al cluster $C_k$ que da valor mínimo de $SSE_{i,k}$.

5.Una vez realizado el procedimiento anterior para todos los puntos que han cambiado de cluster, éstos se asignan a sus clusters definitivos y se da el bucle por completado.

MacQueen: es el mismo método que el de Lloyd salvo por el hecho de que no se recalculan todos los clusters y sus centros de golpe, sino elemento a elemento. Es decir, se empieza igual que en los dos algoritmos anteriores: se escogen $k$ centros, se calculan las distancias euclídeas de cada punto a cada centro, se asigna a cada centro el cluster de puntos que están más cerca de él que de los otros centros, y se sustituye cada centro por el punto medio de los puntos asignados a su cluster. A partir de aquí, en pasos sucesivos se itera el bucle siguiente (recordemos que los puntos a clasificar son $\mathbf{x}_1,\ldots,\mathbf{x}_n$, y los supondremos ordenados por su fila en la tabla de datos):
- Para cada $i=1,\ldots,n$, se mira si el punto $\mathbf{x}_i$ está más cerca del centro de otro cluster que del centro del cluster al que está asignado.
- Si no lo está, se mantiene en su cluster y se pasa al punto siguiente, $\mathbf{x}_{i+1}$. Si se llega al final de la lista de puntos y todos se mantienen en sus clusters, el algoritmo se para.
- Si $\mathbf{x}_i$ está más cerca de otro centro, se traslada al cluster definido por este centro, se recalculan los centros de los dos clusters afectados (el que ha abandonado $\mathbf{x}_i$ y aquél al que se ha incorporado), y se reinicia el bucle, empezando de nuevo con $\mathbf{x}_1$.

El clustering resultante está formado por los clusters existentes en el momento de parar.

La salida del algoritmo de $k$-medias con R tiene las componentes siguientes: (supongamos que hemos guardado en el objeto resultado.km la salida del algoritmo de $k$-medias aplicado a nuestra tabla de datos)

resultado.km$size: nos da los números de objetos, es decir, los tamaños de cada cluster.
resultado.km$cluster: nos dice qué cluster pertenece cada uno de los objetos de nuestra tabla de datos.
resultado.km$centers: nos da los centros de cada cluster en filas. Es decir, la fila 1 sería el centro del cluster 1, la fila 2, del cluster 2 y así sucesivamente.
resultado.km$withinss: nos da las sumas de cuadrados de cada cluster, lo que antes hemos denominado $SS_{C_j}$, para $j=1,\ldots,k$.
resultado.km$tot.withinss: la suma de cuadrados de todos los clusters, lo que antes hemos denominado $SS_C$. También se puede calcular sumando las sumas de los cuadrados de cada cluster: sum(resultado.km$withinss).
resultado.km$totss: es la suma de los cuadrados de las distancias de los puntos en su punto medio de todos estos puntos. Es decir, seria la suma de los cuadrados $SS_C$ pero suponiendo que sólo hubiera un sólo cluster.
resultado.km$betweenss es la diferencia entre resultado.km$totss y resultado.km$tot.withinss y puede demostrarse (es un cálculo bastante tedioso) que es igual a la suma, ponderada por el número de objetos del cluster correspondiente, de los cuadrados de las distancias de los centros de los clusters al punto medio de todos los puntos.

Es decir:

sean $n_1,\ldots, n_k$ los números de objectos de los clusters $C_1,\ldots, C_k$,
sean $\mathbf{x}_{i1},\ldots,\mathbf{x}_{in_i}$ los objectos pertenecientes al cluster $C_i$,
sean $\mathbf{\overline{x}}_1,\ldots,\mathbf{\overline{x}}_k$, los centros de los clusters $C_1,\ldots, C_k$: $\mathbf{\overline{x}}_i =\frac{1}{n_i}\sum\limits_{j=1}^{n_i}\mathbf{x}_{ij},\ i=1,\ldots,k,$
sea $\mathbf{x}$ el punto medio de todos los puntos: $\overline{x}=\frac{1}{n}\sum\limits_{i=1}^k\sum\limits_{j=1}^{n_i} \mathbf{x}_{ij}$.

Entonces: \[ \verb+resultado.km$betweenss+=\sum_{i=1}^{k} n_i \|\mathbf{\overline{x}}_i-\mathbf{x}\|^2. \]

Podríamos considerar la medida anterior como una medida de dispersión de los centros o una medida de cuan separados están los clusters ya que cuanto mayor sea resultado.km$betweenss más separados estarán los centros del punto medio global de todos los puntos y mayor separación habrá entre los clusters.

Entonces, nos interesa el cociente resultado.km$betweenss/resultado.km$totss, que mide la fracción de la variabilidad de los datos que explican los clusters. Cuanto mayor mejor.

Ejemplo

Apliquemos el algoritmo de $k$-medias en R a la tabla de datos trees usando la variante del algoritmo de McQueen con $k=3$ clusters

resultado.km.trees=kmeans(trees,centers=3,algorithm = 'MacQueen')
resultado.km.trees

## K-means clustering with 3 clusters of sizes 19, 7, 5
## 
## Cluster means:
##   Girth Height Volume
## 1 12.52  76.47  25.32
## 2 17.94  81.00  55.93
## 3  9.44  67.20  12.56
## 
## Clustering vector:
##  [1] 3 3 3 3 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2
## 
## Within cluster sum of squares by cluster:
## [1] 1335.0  737.9  100.5
##  (between_SS / total_SS =  77.4 %)
## 
## Available components:
## 
## [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
## [6] "betweenss"    "size"         "iter"         "ifault"

resultado.km.trees=kmeans(trees,centers=3,algorithm = 'MacQueen')
resultado.km.trees

## K-means clustering with 3 clusters of sizes 23, 7, 1
## 
## Cluster means:
##   Girth Height Volume
## 1 11.70  74.65  21.98
## 2 17.29  78.86  50.40
## 3 20.60  87.00  77.00
## 
## Clustering vector:
##  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 3
## 
## Within cluster sum of squares by cluster:
## [1] 2177.8  397.2    0.0
##  (between_SS / total_SS =  73.2 %)
## 
## Available components:
## 
## [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
## [6] "betweenss"    "size"         "iter"         "ifault"

Vemos que R nos ha dado 3 clusters de 23, 7 y 1 elementos cada uno.

Recordemos que el vector resultado.km.trees$cluster nos dice a qué cluster pertenece cada uno de los 31 árboles de nuestra tabla de datos.

Por ejemplo los árboles enumerados como

which(resultado.km.trees$cluster==1)

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

están en el cluster número 1, los árboles enumerados como

which(resultado.km.trees$cluster==2)

## [1] 24 25 26 27 28 29 30

están en el cluster número 2

y los árboles enumerados como

which(resultado.km.trees$cluster==3)

## [1] 31

están en el cluster número 3.

El centro del cluster número 1 ha sido:

resultado.km.trees$centers[1,]

##  Girth Height Volume 
##  11.70  74.65  21.98

El centro del cluster número 2 ha sido:

resultado.km.trees$centers[2,]

##  Girth Height Volume 
##  17.29  78.86  50.40

y el del cluster 3,

resultado.km.trees$centers[3,]

##  Girth Height Volume 
##   20.6   87.0   77.0

Las sumas de cuadrados de cada cluster $SS_{C_1}$, $SS_{C_2}$ y $SS_{C_3}$ son las siguientes:

resultado.km.trees$withinss

## [1] 2177.8  397.2    0.0

La suma de cuadrados de todos los clusters vale, en nuestro caso:

sum(resultado.km.trees$withinss)

## [1] 2575

resultado.km.trees$tot.withinss

## [1] 2575

El valor resultado.km.trees$totss nos da la suma de los cuadrados $SS_C$ pero suponiendo que sólo hubiera un cluster:

resultado.km.trees$totss

## [1] 9620

La dispersión de los centros de los clusters respecto del punto medio de todos los árboles vale:

resultado.km.trees$betweenss

## [1] 7044

Comprobemos la expresión vista anteriormente:

(centro.global=apply(trees,2,mean))

##  Girth Height Volume 
##  13.25  76.00  30.17

sum(resultado.km.trees$size*apply((t(resultado.km.trees$centers)-centro.global)^2,2,sum))

## [1] 7044

En este caso, los clusters han explicado un 73.23% de la variabilidad total de los puntos.

Tal como hemos indicado anteriormente, ejecutar sólo una vez el algoritmo de $k$-means no es aconsejable ya que no tenemos asegurado que hemos llegado al mínimo.

Por dicho motivo, ejecutemos el algoritmo de $k$-means sobre la tabla de datos trees 50 veces a ver si podemos obtener un mínimo más óptimo:

veces=50
SSCs=c()
for (i in 1:veces){
  SSCs=c(SSCs,kmeans(trees,3,algorithm = "MacQueen")$tot.withinss)
}
(min(SSCs))

## [1] 1861

¡Uy!, no habíamos llegado al mínimo. Ahora sabemos que hay un mínimo más óptimo que el hallado anteriormente.

9.3 Clustering jerárquico

En esta parte vamos a introducir un tipo de clustering que, en lugar de darnos los clusters de la partición de objetos, va a darnos un árbol binario que nos va a indicar cómo se van agrupando los objetos de nuestra tabla de datos.

De cara a no extendernos demasiado, vamos a describir con todo detalle los métodos aglomerativos al ser los más usados tanto en técnicas de machine learning como en la literatura.

Otra diferencia a tener en cuenta con respecto a los métodos de partición es que los métodos de clustering jerárquico dan el árbol binario de clasificación a partir de una matriz de distancias entre los objetos de nuestra tabla de datos, no a partir de la tabla de datos misma, tal como hacíamos con el algoritmo de $k$-medias.

Por tanto, antes de empezar a aplicar las técnicas del clustering jerárquico, hemos de hallar una matriz de distancias entre los objectos de nuestra tabla de datos.

En resumen, los métodos jerárquicos parten de una matriz $\mathbf{D}$ de distancias entre los $n$ objetos de nuestra tabla de datos. \[ \mathbf{D}=\left(\begin{array}{cccc} d_{11} & d_{12} & \ldots & d_{1n}\\ d_{21} & d_{22} & \ldots & d_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ d_{n1} & d_{n2} & \ldots & d_{nn} \end{array} \right), \] dónde cada $d_{ij}$ es la distancia o el parecido entre el objeto $i$ y lo objeto $j$.

9.3.1 Distancias

A continuación, especifiquemos la definición general de distancia en un conjunto $X$:

Definición. Una distancia sobre un conjunto $X$ de objetos es una aplicación $d:X\times X\to [0,\infty[$ que satisface las condiciones siguientes:

Separación: $d(x,y)=0$ si, y sólo si, $x=y$.
Simetría: dados dos objectos cualesquiera $x,y\in X$, $d(x,y)=d(y,x)$.
Desigualdad triangular: dados tres objectos cualesquiera $x,y,z\in X$, se verifica $d(x,z)\leq d(x,y)+d(y,z)$.

Diremos que dos objetos $x,y$ son más parecidos o más cercanos cuanto más pequeña es $d(x,y)$, la distancias entre ellos.

Si tenemos una tabla de datos, el conjunto $X$ será un conjunto finito formado por los $n$ objetos o las $n$ filas de la tabla de datos: $X=\{\mathbf{x}_1,\ldots,\mathbf{x}_n\}$.

Por tanto, dar una distancia sobre $X$ es equivalente a dar una matriz $\mathbf{D}$ de $n$ filas y $n$ columnas, donde la componente $i,j$ de dicha matriz, $d_{ij}=d(\mathbf{x}_i,\mathbf{x}_j)$, sería la distancia entre el objeto $i$ y el objeto $j$-ésimo.

Usando la definición de distancia vista anteriormente, tendremos que dicha matriz $\mathbf{D}$ debe ser

simétrica: $d(\mathbf{x}_i,\mathbf{x}_j)=d(\mathbf{x}_j,\mathbf{x}_i)$, para cualquier $i$ y $j$,
cumplir la desigualdad triangular: $d(\mathbf{x}_i,\mathbf{x}_k)\leq d(\mathbf{x}_i,\mathbf{x}_j)+d(\mathbf{x}_j,\mathbf{x}_k)$, para cualquier $i, j, k$.

La primera decisión a tomar cuando queramos realizar un clustering jerárquico es elegir la distancia que vamos a usar.

Es una decisión muy importante ya que dicha decisión determinará el árbol binario que vamos a obtener y dará un significado u otro a los clusters que se deriven del mismo.

La distancia a elegir dependerá del tipo de datos con los que trabajemos. Más concretamente, vamos a distinguir dos tipos de datos: binarios y continuos.

El significado de las distancias dependerá del tipo de datos con los que trabajemos.

9.3.2 Datos binarios

Supongamos que las variables de nuestra matriz de datos sólo contiene datos binarios, es decir, datos con sólo dos posibles valores: 0/1, ausencia/presencia, éxito/fracaso, etc.

Usar por ejemplo la distancia euclídea en este tipo de datos no tendría ningún sentido ya que los valores 0 y 1 no tienen ningún significado numérico.

Para fijar ideas, supongamos que nuestra tabla de datos tiene $n$ filas (objetos) y $m$ columnas (variables), donde los valores $x_{ij}$ valen 0 o 1, $i=1\ldots,n$, $j=1,\ldots,m$.

Consideramos los valores de dos objectos cualesquiera $\mathbf{x}_i =(x_{i1},\ldots,x_{im})$, $\mathbf{x}_j =(x_{j1},\ldots,x_{jm})$ y queremos medir de alguna manera lo parecidos que son dichos objetos.

Para ello, definimos primeramente las cantidades siguientes: \[ \begin{array}{l} a_0 = \left|\{k\mid x_{ik}=x_{jk}=0\}\right|,\\ a_1 =\left|\{k\mid x_{ik}=x_{jk}=1\}\right|, \\ a_2 = \left|\{k\mid x_{ik}\neq x_{jk}\}\right|. \end{array} \] Es decir, $a_0$ serían el número de variables en los que los objetos $i$ y $j$ tienen el valor 0, $a_1$, el número de variables en los que los objetos $i$ y $j$ tienen el valor $1$ y $a_2$, el número de variables en los que los objetos $i$ y $j$ difieren.

Intuitivamente, cuanto mayores sean $a_0$ y $a_1$ y cuanto menor sea $a_2$, más parecidos deben ser los objetos $i$ y $j$.

Basándonos en la consideración anterior, definimos el “parecido” o la distancia entre los objetos $i$ y $j$ como: \[ \sigma_{ij}=\frac{a_1 + \delta a_0}{\alpha a_1 + \beta a_0 +\lambda a_2}, \] donde los parámetros $\alpha$, $\beta$, $\delta$ y $\lambda$ son valores a elegir que nos determinarán la distancia entre los objetos $i$ y $j$.

Fijarse que el numerador de la distancia $\sigma_{ij}$ sólo depende del número de variables coincidentes $a_0$ y $a_1$ y el denominador depende de todas, tanto las coincidentes $a_0$ y $a_1$ como la disidente $a_2$.

Los valores más comunes de los parámetros anteriores junto con sus nombres se presentan en la tabla siguiente:

Nombre	$\delta$	$\lambda$	$\alpha$	$\beta$	Definición
Hamming	$1$	$1$	1	1	$\dfrac{a_1 + a_0}{a_0+a_1+a_2}$
Jaccard	$0$	$1$	1	0	$\dfrac{a_1}{a_1 + a_2}$
Tanimoto	$1$	$2$	1	1	$\dfrac{a_1+a_0}{a_1+2a_2+a_0}$
Rusell–Rao	0	1	1	1	$\dfrac{a_1}{a_0+a_1+a_2}$
Dice	$0$	$0.5$	1	0	$\dfrac{2a_1}{2a_1 + a_2}$
Kulczynski	0	1	0	0	$\dfrac{a_1}{a_2}$

Ejemplo

La tabla de datos Arrests de la librería car nos da la información de 5226 arrestos en Toronto por posesión de cantidades pequeñas de marihuana.

En este ejemplo nos interesan las siguientes variables binarias:

colour: la raza del arrestado/a con niveles Black y White.
sex: el sexo del arrestado/a con niveles Female y Male.
employed: si el arrestado/a tenía empleo con niveles No y Yes.
citizen: si el arrestado/a era ciudadano/a de Toronto con niveles No y Yes.

Como dicha tabla de datos contiene muchos individuos, vamos a considerar sólo una muestra de 25 individuos:

library(car)
set.seed(888)  ## Fijamos la semilla
individuos.elegidos = sample(1:5226,25)
tabla.arrestados = Arrests[individuos.elegidos,c("colour","sex","employed","citizen")]
rownames(tabla.arrestados)=1:25

Los 10 primeros individuos de nuestra tabla de datos son:

head(tabla.arrestados,10)

##    colour    sex employed citizen
## 1   White   Male       No     Yes
## 2   White   Male      Yes     Yes
## 3   White   Male      Yes     Yes
## 4   White   Male      Yes     Yes
## 5   White   Male      Yes     Yes
## 6   White   Male      Yes     Yes
## 7   White   Male      Yes     Yes
## 8   White Female       No     Yes
## 9   Black   Male      Yes     Yes
## 10  Black   Male      Yes     Yes

Vamos a hallar la matriz de distancias de Hamming entre los 25 individuos.

En primer lugar, codificamos los valores de los niveles de las variables de nuestra tabla de datos de la forma siguiente:

colour: White=0, Black=1.
sex: Male=0, Female=1.
employed: No=0, Yes=1.
citizen: No=0, Yes=1.

tabla.arrestados$colour = ifelse(tabla.arrestados$colour=="White",0,1)
tabla.arrestados$sex = ifelse(tabla.arrestados$sex=="Male",0,1)
tabla.arrestados$employed = ifelse(tabla.arrestados$employed=="No",0,1)
tabla.arrestados$citizen = ifelse(tabla.arrestados$citizen=="No",0,1)

En segundo lugar, definimos la función siguientes para que nos dé los valores $a_0$, $a_1$ y $a_2$ dados un par de individuos $i$ y $j$:

as = function(xi,xj){
  n=length(xi)
  a0 = length(which(xi==xj & xi==0))
  a1 = length(which(xi==xj & xi==1))
  a2 = length(which(xi!=xj))
  return(c(a0,a1,a2))
  }

Recordemos que la distancia de Hamming vale $\sigma_{ij}=\frac{a_1+a_0}{a_0+a_1+a_2}$:

n=dim(tabla.arrestados)[1]
matriz.dist.hamming=matrix(1,n,n)
for (i in 1:(n-1)){
  for (j in (i+1):n){
    aux=as(tabla.arrestados[i,],tabla.arrestados[j,])
    matriz.dist.hamming[i,j]=(aux[1]+aux[2])/sum(aux)
    matriz.dist.hamming[j,i]=matriz.dist.hamming[i,j]
  }
}

La distancia de Hamming de los 10 primeros individuos vale:

matriz.dist.hamming[1:10,1:10]

##       [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
##  [1,] 1.00 0.75 0.75 0.75 0.75 0.75 0.75 0.75 0.50  0.50
##  [2,] 0.75 1.00 1.00 1.00 1.00 1.00 1.00 0.50 0.75  0.75
##  [3,] 0.75 1.00 1.00 1.00 1.00 1.00 1.00 0.50 0.75  0.75
##  [4,] 0.75 1.00 1.00 1.00 1.00 1.00 1.00 0.50 0.75  0.75
##  [5,] 0.75 1.00 1.00 1.00 1.00 1.00 1.00 0.50 0.75  0.75
##  [6,] 0.75 1.00 1.00 1.00 1.00 1.00 1.00 0.50 0.75  0.75
##  [7,] 0.75 1.00 1.00 1.00 1.00 1.00 1.00 0.50 0.75  0.75
##  [8,] 0.75 0.50 0.50 0.50 0.50 0.50 0.50 1.00 0.25  0.25
##  [9,] 0.50 0.75 0.75 0.75 0.75 0.75 0.75 0.25 1.00  1.00
## [10,] 0.50 0.75 0.75 0.75 0.75 0.75 0.75 0.25 1.00  1.00

9.3.3 Datos continuos

Supongamos ahora que nuestra matriz de datos contiene datos continuos, es decir, los objectos a clasificar se pueden considerar elementos de $\mathbb{R}^m$, donde recordemos que tenemos $n$ individuos u objetos y $m$ variables.

El significado de distancia en este caso es el opuesto al significado de distancia en el caso de datos binarios.

Ahora en el caso de datos continuos, cuanto mayor sea la distancia entre dos objetos, más disimilares son y cuanto menor sea, más similares serán.

En este caso, las distancias que se definen entre los objectos se basan en las llamadas normas $L_r$.

Más concretamente, dados dos objectos $\mathbf{x}_i$ y $\mathbf{x}_j$ de componentes, \[ \mathbf{x}_i=(x_{i1},\ldots,x_{im}),\ \mathbf{x}_j=(x_{j1},\ldots,x_{jm}), \] la distancia $L_r$ entre dichos objetos se define como: \[ d_{ij}=\|\mathbf{x_i} - \mathbf{x_j}\|_r = \left(\sum_{k=1}^m |x_{ik} - x_{jk}|^r\right)^{1/r} \]

Cuando $r=1$, la distancia anterior: $d_{ij}= \sum\limits_{k=1}^m |x_{ik} - x_{jk}|,$ se denomina distancia de Manhattan y cuando $r=2$, $d_{ij}= \sqrt{\sum\limits_{k=1}^m (x_{ik} - x_{jk})^2}$, distancia euclídea.

Ejemplo

Para ilustrar el cálculo de distancias en caso de variables continuas, vamos a considerar la tabla de datos iris vista ya anteriormente y vamos a elegir aleatoriamente 10 flores al azar:

set.seed(2020)
flores.elegidas = sample(1:150,10)
tabla.iris = iris[flores.elegidas,]
rownames(tabla.iris)=1:10

Vamos a calcular la matriz de distancias euclídeas entre las 30 flores anteriores usando las 4 variables continuas de la tabla de datos: la longitud y la amplitud del sépalo y del pétalo.

En primer lugar definimos una función que nos calcula la distancia euclídea entre dos vectores:

dist.euclidea = function(x,y){
  n=length(x)
  d = sqrt(sum((x-y)^2))
  return(d)
}

La matriz de distancias será la siguiente:

n=dim(tabla.iris)[1]
matriz.dist.iris = matrix(0,n,n)
for (i in 1:(n-1)){
  for (j in (i+1):n){
    matriz.dist.iris[i,j]=dist.euclidea(tabla.iris[i,1:4],tabla.iris[j,1:4])
    matriz.dist.iris[j,i]=matriz.dist.iris[i,j]
  }
}

Las distancias entre las 10 primeras flores vale:

round(matriz.dist.iris,2)

##       [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
##  [1,] 0.00 3.79 1.58 3.89 1.29 0.71 1.08 4.30 1.71  3.86
##  [2,] 3.79 0.00 2.47 0.41 4.94 3.87 3.31 1.54 2.44  0.39
##  [3,] 1.58 2.47 0.00 2.67 2.54 1.48 0.91 2.80 0.45  2.54
##  [4,] 3.89 0.41 2.67 0.00 5.09 4.03 3.51 1.84 2.64  0.58
##  [5,] 1.29 4.94 2.54 5.09 0.00 1.19 1.74 5.23 2.63  5.00
##  [6,] 0.71 3.87 1.48 4.03 1.19 0.00 0.78 4.27 1.71  3.97
##  [7,] 1.08 3.31 0.91 3.51 1.74 0.78 0.00 3.60 1.06  3.38
##  [8,] 4.30 1.54 2.80 1.84 5.23 4.27 3.60 0.00 2.62  1.31
##  [9,] 1.71 2.44 0.45 2.64 2.63 1.71 1.06 2.62 0.00  2.44
## [10,] 3.86 0.39 2.54 0.58 5.00 3.97 3.38 1.31 2.44  0.00

9.3.4 Cálculo de distancias en `R`

La matriz de distancias $\mathbf{D}$ entre los objetos de nuestra tabla de datos se puede calcular con la función dist, cuya sintaxis básica es:

dist(x, method=...)

donde:

x es nuestra tabla de datos (una matriz o un data frame de variables cuantitativas).
method sirve para indicar la distancia que queremos usar, cuyo nombre se ha de entrar entrecomillado. La distancia por defecto es la euclídea que hemos venido usando hasta ahora. Otros posibles valores son (en lo que sigue, $\mathbf{x}=(x_1,\ldots,x_m)$ e $y=(y_1,\ldots,y_m)$ son dos vectores de $\mathbb{R}^m$):
- La distancia de Manhattan, manhattan, que recordemos que vale $\sum\limits_{i=1}^m |x_i-y_i|$.
- La distancia del máximo, maximum, que vale: $\max_{i=1,\ldots,m}|x_i-y_i|$.
- La distancia de Canberra, canberra, que vale $\sum\limits_{i=1}^m \frac{|x_i-y_i|}{|x_i|+|y_i|}$.
- La distancia de Minkowski, minkowski, que depende de un parámetro $p>0$ (que se ha de especificar en la función dist con p igual a su valor), y que vale: $\left(\sum_{i=1}^m |x_{i} - y_{i}|^p\right)^{1/p}$. Observad que cuando $p=1$ se obtiene la distancia de Manhattan y cuando $p=2$, la distancia euclídea usual.
- La distancia binaria, binary, que sirve básicamente para comparar vectores binarios (si los vectores no son binarios, R los entiende como binarios sustituyendo cada entrada diferente de 0 por 1). La distancia binaria entre x e y binarios es el número de posiciones en las que estos vectores tienen entradas diferentes, dividido por el número de posiciones en las que alguno de los dos vectores tiene un 1.

La salida de aplicar la función dist a nuestra tabla de datos es un objeto dist de R, no es una matriz de distancias usual.

Calculemos la matriz de distancias en el ejemplo anterior.

La matriz de distancias con la distancia euclídea de la tabla de datos de las 30 flores anteriores vale:

round(dist(tabla.iris[,1:4]),2)

##       1    2    3    4    5    6    7    8    9
## 2  3.79                                        
## 3  1.58 2.47                                   
## 4  3.89 0.41 2.67                              
## 5  1.29 4.94 2.54 5.09                         
## 6  0.71 3.87 1.48 4.03 1.19                    
## 7  1.08 3.31 0.91 3.51 1.74 0.78               
## 8  4.30 1.54 2.80 1.84 5.23 4.27 3.60          
## 9  1.71 2.44 0.45 2.64 2.63 1.71 1.06 2.62     
## 10 3.86 0.39 2.54 0.58 5.00 3.97 3.38 1.31 2.44

Si queremos transformar la salida de la matriz de distancias anterior a una matriz de distancias “usual” hay que aplicarle la función as.matrix:

round(as.matrix(dist(tabla.iris[,1:4])),2)

##       1    2    3    4    5    6    7    8    9   10
## 1  0.00 3.79 1.58 3.89 1.29 0.71 1.08 4.30 1.71 3.86
## 2  3.79 0.00 2.47 0.41 4.94 3.87 3.31 1.54 2.44 0.39
## 3  1.58 2.47 0.00 2.67 2.54 1.48 0.91 2.80 0.45 2.54
## 4  3.89 0.41 2.67 0.00 5.09 4.03 3.51 1.84 2.64 0.58
## 5  1.29 4.94 2.54 5.09 0.00 1.19 1.74 5.23 2.63 5.00
## 6  0.71 3.87 1.48 4.03 1.19 0.00 0.78 4.27 1.71 3.97
## 7  1.08 3.31 0.91 3.51 1.74 0.78 0.00 3.60 1.06 3.38
## 8  4.30 1.54 2.80 1.84 5.23 4.27 3.60 0.00 2.62 1.31
## 9  1.71 2.44 0.45 2.64 2.63 1.71 1.06 2.62 0.00 2.44
## 10 3.86 0.39 2.54 0.58 5.00 3.97 3.38 1.31 2.44 0.00

9.3.5 Escalado de los datos

En el caso de que no queramos que la variación de las variables no influya en el posterior análisis del cálculo del árbol binario debido a que los datos están en escalas diferentes o para que la contribución a la matriz de distancias de cada una de las variables sea parecida, es conveniente que los datos estén en la misma escala.

En este caso, se escalan los datos de la forma siguiente: a los datos de la variable $k$ o columna $k$, $x_{ik}$, $i=1,\ldots,n$ se les resta la media de dicha variable $\overline{x}_k =\frac{\sum\limits_{i=1}^n x_{ik}}{n}$ y se dividen por su desviación estándar $\tilde{s}_k=\sqrt{\frac{n}{n-1}\left(\frac{\sum\limits_{i=1}^n x_{ik}^2}{n}-\overline{x}_k^2\right)}$:

\[ \tilde{x}_{ik}=\frac{x_{ik}-\overline{x}_k}{\tilde{s}_k}, \] donde $\tilde{x}_{ik}$ serían los nuevos valores de la tabla de datos escalada.

De esta forma, todas las $m$ variables o columnas de nuestra tabla de datos tendrán media 0 y desviación estándar 1.

Observación: Cuando usamos la distancia euclídea, la distancia entre los objetos $i$ y $j$ escalados puede calcularse a partir de los valores iniciales $x_{ik}$ y $y_{jk}$, $k=1,\ldots,m$ de la forma siguiente: \[ d_{ij}= \sqrt{\sum_{k=1}^n \frac{(x_{ik} - x_{jk})^2}{\tilde{s}^2_{k}}}. \]

Para escalar los datos en R hemos de usar la función scale:

scale(x, center = TRUE, scale = TRUE)

donde:

x: nuestra tabla de datos.
center: es un parámetro lógico o un vector numérico de longitud el número de columnas de x indicando la cantidad que queremos restar a los valores de cada variable o columna. Si vale TRUE que es su valor por defecto, a cada columna se le resta la media de dicha columna.
scale: es un parámetro lógico o un vector numérico de longitud el número de columnas de x indicando la cantidad por la que queremos dividir los valores de cada variable o columna. Si vale TRUE que es su valor por defecto, a los valores de cada columna se les divide por la desviación estándar de dicha columna.

Las desviaciones estándar de las variables de la tabla de datos de la muestra de flores iris que hemos trabajado son bastante diferentes:

apply(tabla.iris[,1:4],2,sd)

## Sepal.Length  Sepal.Width Petal.Length  Petal.Width 
##       0.6913       0.5181       1.7373       0.6289

Si no queremos que la variación de los datos intervenga en el análisis posterior que vamos a hacer, tenemos que escalar los datos:

tabla.iris.escalada = scale(tabla.iris[,1:4])

Comprobemos que las variables de la tabla de datos nueva tienen media 0 y desviación estándar 1:

apply(tabla.iris.escalada,2,mean)

##            Sepal.Length             Sepal.Width            Petal.Length 
##  0.00000000000000013601 -0.00000000000000006665  0.00000000000000002776 
##             Petal.Width 
##  0.00000000000000002219

apply(tabla.iris.escalada,2,sd)

## Sepal.Length  Sepal.Width Petal.Length  Petal.Width 
##            1            1            1            1

9.3.6 Clustering jerárquico aglomerativo

Una vez explicado con todo detalle cómo realizar el cálculo de una matriz de distancias a partir de una tabla de datos, vamos a desarrollar los pasos de los que consta el clustering jerárquico aglomerativo.

Recordemos que la salida del algoritmo del clustering jerárquico aglomerativo es un árbol binario donde se va indicando cómo se van agrupando los clusters partiendo de una configuración inicial en la que cada objeto forma un cluster.

Los pasos del algoritmo son los siguientes:

Suponemos que partimos de $n$ objetos, y de una matriz de distancias $\mathbf{D}$ de dimensiones $n\times n$, es decir, $n$ filas y $n$ columnas.
En el primer paso, suponemos que cada objeto forma un cluster inicial.
En el segundo paso, hallamos los dos clusters $C_1$ y $C_2$ cuya distancia sea la más pequeña de entre todos los pares de clusters. Si hay pares de clusters que empatan en la distancia mínima, escogemos un par al azar. Seguidamente, unimos $C_1$ y $C_2$ en un cluster nuevo que denotamos $C_1+C_2$. ¡Ojo, la suma no significa sumar en el sentido clásico sino unir!
Los clusters $C_1$ y $C_2$ que hemos unido en el paso anterior ya no existen. Por tanto, en el tercer paso, los eliminamos de la lista de clusters.
En el cuarto paso, recalculamos la distancia del nuevo cluster $C_1+C_2$ a los demás clusters tal como indicaremos más adelante. Tendremos una matriz de distancias $\mathbf{D'}$ con una fila menos y una columna menos.
Repetimos los pasos 2, 3 y 4 hasta que sólo queda un único cluster y una matriz de distancias que sea un único número.

Tal como hemos comentado en el algoritmo anterior, falta indicar en el cuarto paso cómo se calcula la distancia del nuevo cluster $C_1+C_2$ a los demás clusters. Dicha distancia se puede calcular de varias maneras, dando lugar a resultados diferentes o a tipos de clusters diferentes:

Por enlace simple: la distancia entre dos clusters $C$ y $C'$ cualquiera se calcula como: $d(C,C')=\min\{d(a,b)\mid a\in C,b\in C'\}$.

Por tanto, la distancia del nuevo cluster $C_1+C_2$ a un cluster $C$ sería: \[ d(C,C_1+ C_2)=\min\{d(C,C_1),d(C,C_2)\}. \]

Por enlace completo: la distancia entre dos clusters $C$ y $C'$ cualquiera se calcula como: $d(C,C')=\max\{d(a,b)\mid a\in C,b\in C'\}$.

Por tanto, la distancia del nuevo cluster $C_1+C_2$ a un cluster $C$ sería: \[d(C,C_1+ C_2)=\max\{d(C,C_1),d(C,C_2)\}.\]

Por enlace medio: la distancia entre dos clusters $C$ y $C'$ cualquiera se calcula como: $\displaystyle d(C,C')=\displaystyle\frac{\sum\limits_{a\in C, b\in C'} d(a,b)}{|C|\cdot |C'|},$ donde $|C|$ indica el tamaño del cluster $C$ o el número de elementos del mismo.

Por tanto, la distancia del nuevo cluster $C_1+C_2$ a un cluster $C$ sería: \[ d(C,C_1+ C_2)=\frac{|C_1|}{|C_1|+|C_2|}d(C,C_1)+\frac{|C_2|}{|C_1|+|C_2|}d(C,C_2). \]

Las expresiones anteriores son casos particulares de la siguiente regla general: suponiendo conocidas las distancias siguientes: \[ d(C,C_1),\quad d(C,C_2),\quad d(C_1,C_2), \] la formula genérica para hallar $d(C,C_1+ C_2)$ es la siguiente: \[ \begin{array}{rl} d(C,C_1+C_2) = & \delta_1 d(C,C_1)+\delta_2 d(C,C_2)+\delta_3 d(C_1,C_2) \\ & + \delta_0 |d(C,C_1)-d(C,C_2)|, \end{array} \] donde los $\delta_i$ son parámetros a elegir. Cada elección da lugar a un algoritmo diferente, con resultados posiblemente diferentes como se muestra en la tabla siguiente:

Nombre	$\delta_1$	$\delta_2$	$\delta_3$	$\delta_0$
Enlace simple	$1/2$	$1/2$	$0$	$-1/2$
Enlace completo	$1/2$	$1/2$	$0$	$1/2$
Enlace promedio	$\frac{\|C_1\|}{\|C_1\| + \|C_2\|}$	$\frac{\|C_2\|}{\|C_1\|+ \|C_2\|}$	$0$	$0$
Centroide	$\frac{\|C_1\|}{\|C_1\| + \|C_2\|}$	$\frac{\|C_2\|}{\|C_1\| + \|C_2\|}$	$-\frac{\|C_1\| \|C_2\|}{(\|C_1\| + \|C_2\|)^2}$	$0$
Mediana	$1/2$	$1/2$	$-1/4$	$0$
Ward	$\frac{\|C\| + \|C_1\|}{\|C\| + \|C_1\| + \|C_2\|}$	$\frac{\|C\| + \|C_2\|}{\|C\| + \|C_1\|+ \|C_2\|}$	$-\frac{\|C\|}{\|C\| + \|C_1\| + \|C_2\|}$	$0$

Ejercicio

Demostrar que para el enlace simple y para el enlace completo las fórmulas dadas anteriormente y la fórmulas dadas por la tabla anterior son equivalentes.

Más concretamente, demostrar que dados $C_1,C_2$ y $C$ clusters,

Enlace simple: \[ d(C,C_1+ C_2)=\min\{d(C,C_1),d(C,C_2)\}=\frac{1}{2}d(C,C_1)+\frac{1}{2} d(C,C_2)-\frac{1}{2} |d(C,C_1)-d(C,C_2)|. \]
Enlace completo: \[ d(C,C_1+ C_2)=\max\{d(C,C_1),d(C,C_2)\}=\frac{1}{2}d(C,C_1)+\frac{1}{2} d(C,C_2)+\frac{1}{2} |d(C,C_1)-d(C,C_2)|. \]

Ejemplo de la muestra de flores iris

Vamos a aplicar el método del enlace simple a la muestra de flores de la tabla de datos iris.

Usaremos los datos sin escalar. Dejamos como ejercicio repetir este ejemplo con los datos escalados.

Recordemos que la matriz de distancias estaba en la matriz matriz.dist.iris.

Hallemos las dos flores distintas que tienen distancia mínima que no estén en la diagonal ya que los valores de la diagonal en la matriz de distancias valen 0 y éstas no nos interesan ya que corresponden a las distancias entre todas las flores iguales.

Una forma de hacerlo (no la única) es definir otra matriz asignando el valor máximo de nuestra matriz de distancias a los valores de la diagonal y hallar el mínimo de la nueva matriz. De esta manera, no nos saldrán los valores de la diagonal:

matriz.nueva=matriz.dist.iris
diag(matriz.nueva)=max(matriz.dist.iris)
(flores.min=which(matriz.nueva == min(matriz.nueva), arr.ind = TRUE))

##      row col
## [1,]  10   2
## [2,]   2  10

Vemos que las flores 10 y flores 2 son las más cercanas con una distancia de 0.3873.

Definimos el cluster nuevo $\{10,2\}$ y eliminamos las flores 10 y flores 2.

Los nuevos clusters serán:

## [1] 1
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9

## row col 
##  10   2

A continuación tenemos que hallar la distancia del nuevo cluster $\{10,2\}$ a los demás clusters que en este caso serán clusters con una sola flor usando la expresión del enlace simple: $d(C,C_1+ C_2)=\min\{d(C,C_1),d(C,C_2)\}:$

\[ \begin{array}{rl} d(\{1\},\{10,2\}) & =\min\{d(\{1\},\{10\}),d(\{1\},\{2\})\}=\min\{3.8626,3.7908\} = 3.7908,\\ d(\{3\},\{10,2\}) & =\min\{d(\{3\},\{10\}),d(\{3\},\{2\})\}=\min\{2.5417,2.4718\} = 2.4718,\\ d(\{4\},\{10,2\}) & =\min\{d(\{4\},\{10\}),d(\{4\},\{2\})\}=\min\{0.5831,0.4123\} = 0.4123,\\ d(\{5\},\{10,2\}) & =\min\{d(\{5\},\{10\}),d(\{5\},\{2\})\}=\min\{4.998,4.9447\} = 4.9447,\\ d(\{6\},\{10,2\}) & =\min\{d(\{6\},\{10\}),d(\{6\},\{2\})\}=\min\{3.9724,3.8743\} = 3.8743,\\ d(\{7\},\{10,2\}) & =\min\{d(\{7\},\{10\}),d(\{7\},\{2\})\}=\min\{3.3808,3.3136\} = 3.3136,\\ d(\{8\},\{10,2\})& =\min\{d(\{8\},\{10\}),d(\{8\},\{2\})\}=\min\{1.3115,1.5395\} = 1.3115,\\ d(\{9\},\{10,2\}) & =\min\{d(\{9\},\{10\}),d(\{9\},\{2\})\}=\min\{2.4372,2.4352\} = 2.4352. \end{array} \]

La nueva matriz de distancias entre los clusters: \[ \{1\},\ \{3\},\ \{4\},\ \{5\},\ \{6\},\ \{7\},\ \{8\},\ \{9\},\ \{10,2\}, \] es la siguiente:

##        [,1]  [,2]  [,3]  [,4]  [,5]  [,6]  [,7]  [,8]  [,9]
##  [1,] 0.000 1.581 3.886 1.288 0.707 1.082 4.299 1.715 3.791
##  [2,] 1.581 0.000 2.672 2.542 1.483 0.911 2.804 0.447 2.472
##  [3,] 3.886 2.672 0.000 5.085 4.027 3.514 1.838 2.642 0.412
##  [4,] 1.288 2.542 5.085 0.000 1.192 1.741 5.233 2.634 4.945
##  [5,] 0.707 1.483 4.027 1.192 0.000 0.781 4.273 1.709 3.874
##  [6,] 1.082 0.911 3.514 1.741 0.781 0.000 3.596 1.063 3.314
##  [7,] 4.299 2.804 1.838 5.233 4.273 3.596 0.000 2.619 1.311
##  [8,] 1.715 0.447 2.642 2.634 1.709 1.063 2.619 0.000 2.435
##  [9,] 3.791 2.472 0.412 4.945 3.874 3.314 1.311 2.435 0.000

Observamos que tiene una dimensión menor y es una matriz de 9 filas y 9 columnas.

El siguiente paso es hallar los dos clusters siguientes con distancia mínima.

Haremos el mismo truco que hemos hecho anteriormente: (la nueva matriz de distancias la hemos guardado en matriz.dist.iris2)

matriz.nueva=matriz.dist.iris2
diag(matriz.nueva)=max(matriz.dist.iris2)
(flores.min2 = which(matriz.nueva == min(matriz.nueva),arr.ind=TRUE))

##      row col
## [1,]   9   3
## [2,]   3   9

Vemos que los clusters $\{10,2\}$ y $\{4\}$ son las más cercanos con una distancia de 0.4123. Acordarse que la fila 9 correspondía al cluster que hemos unido en el paso anterior $\{10,2\}$.

Definimos el cluster nuevo $\{10,2, 4\}$ y eliminamos los clusters $\{10,2\}$ y $\{4\}$.

Los nuevos clusters serán:

## [1] 1
## [1] 3
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9

## col     row 
##   2   4  10

A continuación tenemos que hallar la distancia del nuevo cluster $\{10,2,4\}$ a los demás clusters que en este caso serán clusters con una sola flor usando la expresión del enlace simple: $d(C,C_1+ C_2)=\min\{d(C,C_1),d(C,C_2)\}:$

\[ \begin{array}{rl} d(\{1\},\{10,2,4\}) & =\min\{d(\{1\},\{10,2\}),d(\{1\},\{4\})\}=\min\{3.7908,3.8859\} = 3.7908,\\ d(\{3\},\{10,2,4\}) & =\min\{d(\{3\},\{10,2\}),d(\{3\},\{4\})\}=\min\{2.4718,2.6721\} = 2.4718,\\ d(\{5\},\{10,2,4\}) & =\min\{d(\{5\},\{10,2\}),d(\{5\},\{4\})\}=\min\{4.9447,5.0853\} = 4.9447,\\ d(\{6\},\{10,2,4\}) & =\min\{d(\{6\},\{10,2\}),d(6\},\{4\})\}=\min\{3.8743,4.0274\} = 3.8743,\\ d(\{7\},\{10,2,4\}) & =\min\{d(\{7\},\{10,2\}),d(\{7\},\{4\})\}=\min\{3.3136,3.5143\} = 3.3136,\\ d(\{8\},\{10,2,4\}) & =\min\{d(\{8\},\{10,2\}),d(\{8\},\{4\})\}=\min\{1.3115,1.8385\} = 1.3115,\\ d(\{9\},\{10,2,4\}) & =\min\{d(\{9\},\{10,2\}),d(\{9\},\{4\})\}=\min\{2.4352,2.642\} = 2.4352. \end{array} \]

La nueva matriz de distancias entre los clusters: \[ \{1\},\ \{3\},\ \{5\},\ \{6\},\ \{7\},\ \{8\},\ \{9\},\ \{10,2,4\}, \] es la siguiente:

##       [,1]  [,2]  [,3]  [,4]  [,5]  [,6]  [,7]  [,8]
## [1,] 0.000 1.581 1.288 0.707 1.082 4.299 1.715 3.791
## [2,] 1.581 0.000 2.542 1.483 0.911 2.804 0.447 2.472
## [3,] 1.288 2.542 0.000 1.192 1.741 5.233 2.634 4.945
## [4,] 0.707 1.483 1.192 0.000 0.781 4.273 1.709 3.874
## [5,] 1.082 0.911 1.741 0.781 0.000 3.596 1.063 3.314
## [6,] 4.299 2.804 5.233 4.273 3.596 0.000 2.619 1.311
## [7,] 1.715 0.447 2.634 1.709 1.063 2.619 0.000 2.435
## [8,] 3.791 2.472 4.945 3.874 3.314 1.311 2.435 0.000

Observamos que tiene una dimensión menor y es una matriz de 8 filas y 8 columnas.

El siguiente paso es hallar los dos clusters siguientes con distancia mínima.

Haremos el mismo truco que hemos hecho en los dos pasos anteriores: (la nueva matriz de distancias la hemos guardado en matriz.dist.iris3)

matriz.nueva=matriz.dist.iris3
diag(matriz.nueva)=max(matriz.dist.iris3)
(flores.min3 = which(matriz.nueva == min(matriz.nueva),arr.ind=TRUE))

##      row col
## [1,]   7   2
## [2,]   2   7

Vemos que los clusters $\{9\}$ y $\{3\}$ son las más cercanos con una distancia de 0.4472.

Definimos el cluster nuevo $\{3,9\}$ y eliminamos los clusters $\{3\}$ y $\{9\}$

Los nuevos clusters serán:

## [1] 1
## [1] 5
## [1] 6
## [1] 7
## [1] 8

## col     row 
##   2   4  10

## [1] 3 9

A continuación tenemos que hallar la distancia del nuevo cluster $\{3,9\}$ a los demás clusters que en este caso serán clusters con una sola flor usando la expresión del enlace simple: $d(C,C_1+ C_2)=\min\{d(C,C_1),d(C,C_2)\}:$

\[ \begin{array}{rl} d(\{1\},\{3,9\}) & =\min\{d(\{1\},\{3\}),d(\{1\},\{9\})\}=\min\{1.7146,1.5811\} = 1.5811,\\ d(\{5\},\{3,9\}) & =\min\{d(\{5\},\{3\}),d(\{5\},\{9\})\}=\min\{2.6344,2.5417\} = 2.5417,\\ d(\{6\},\{3,9\}) & =\min\{d(\{6\},\{3\}),d(\{6\},\{9\})\}=\min\{1.7088,1.4832\} = 1.4832,\\ d(\{7\},\{3,9\}) & =\min\{d(\{7\},\{3\}),d(\{7\},\{9\})\}=\min\{1.063,0.911\} = 0.911,\\ d(\{8\},\{3,9\}) & =\min\{d(\{8\},\{3\}),d(\{8\},\{9\})\}=\min\{2.6192,2.8036\} = 2.6192,\\ d(\{2,4,10\},\{3,9\}) & =\min\{d(\{2,4,10\},\{3\}),d(\{2,4,10\},\{9\})\}=\min\{2.4352,2.4718\} \\ & = 2.4352. \end{array} \]

La nueva matriz de distancias entre los clusters: \[ \{1\},\ \{5\},\ \{6\},\ \{7\},\ \{8\},\ \{2,4,10\},\ \{3,9\}, \] es la siguiente:

##       [,1]  [,2]  [,3]  [,4]  [,5]  [,6]  [,7]
## [1,] 0.000 1.288 0.707 1.082 4.299 3.791 1.581
## [2,] 1.288 0.000 1.192 1.741 5.233 4.945 2.542
## [3,] 0.707 1.192 0.000 0.781 4.273 3.874 1.483
## [4,] 1.082 1.741 0.781 0.000 3.596 3.314 0.911
## [5,] 4.299 5.233 4.273 3.596 0.000 1.311 2.619
## [6,] 3.791 4.945 3.874 3.314 1.311 0.000 2.435
## [7,] 1.581 2.542 1.483 0.911 2.619 2.435 0.000

Observamos que tiene una dimensión menor y es una matriz de 7 filas y 7 columnas.

Y así sucesivamente hasta tener un solo cluster.

9.3.7 Clustering jerárquico aglomerativo con `R`

La función de R para realizar un clustering jerárquico aglomerativo es hclust:

hclust(d, method = ...)

donde:

d es la matriz de distancias entre nuestros objetos calculada con la función dist.
method sirve para especificar cómo se define la distancia de la unión de dos clusters al resto de los clusters. El nombre del método se ha de entrar entrecomillado. Los más populares son los siguientes:
- Método de enlace completo, complete,
- Método de enlace simple, single,
- Método de enlace promedio, average,
- Método de la mediana, median,
- Método del centroide, centroid,
- Método de Ward clásico, ward.D.

Para la interpretación de la salida, imaginemos que hemos guardado en el objeto estudio.clustering el resultado de la función hclust:

estudio.clustering = hclust(d,method=...)

entonces:

estudio.clustering$merge nos indica cómo ha ido agrupando los clusters. Es una matriz de $n-1$ filas y 2 columnas, donde $n$ es el número de objetos. En esta matriz, los objetos originales se representan con números negativos, y los nuevos clusters con números positivos que indican el paso en el que se han creado.
estudio.clustering$height es un vector que contiene las distancias a las que se han ido agrupando los pares de clusters.

Ejemplo de la muestra de flores iris

Para realizar el estudio de la muestra de flores de la tabla de datos iris hacemos los siguiente:

estudio.clustering.iris = hclust(dist(tabla.iris[,1:4]),method="single")

Veamos cómo ha realizado los agrupamientos:

estudio.clustering.iris$merge

##       [,1] [,2]
##  [1,]   -2  -10
##  [2,]   -4    1
##  [3,]   -3   -9
##  [4,]   -1   -6
##  [5,]   -7    4
##  [6,]    3    5
##  [7,]   -5    6
##  [8,]   -8    2
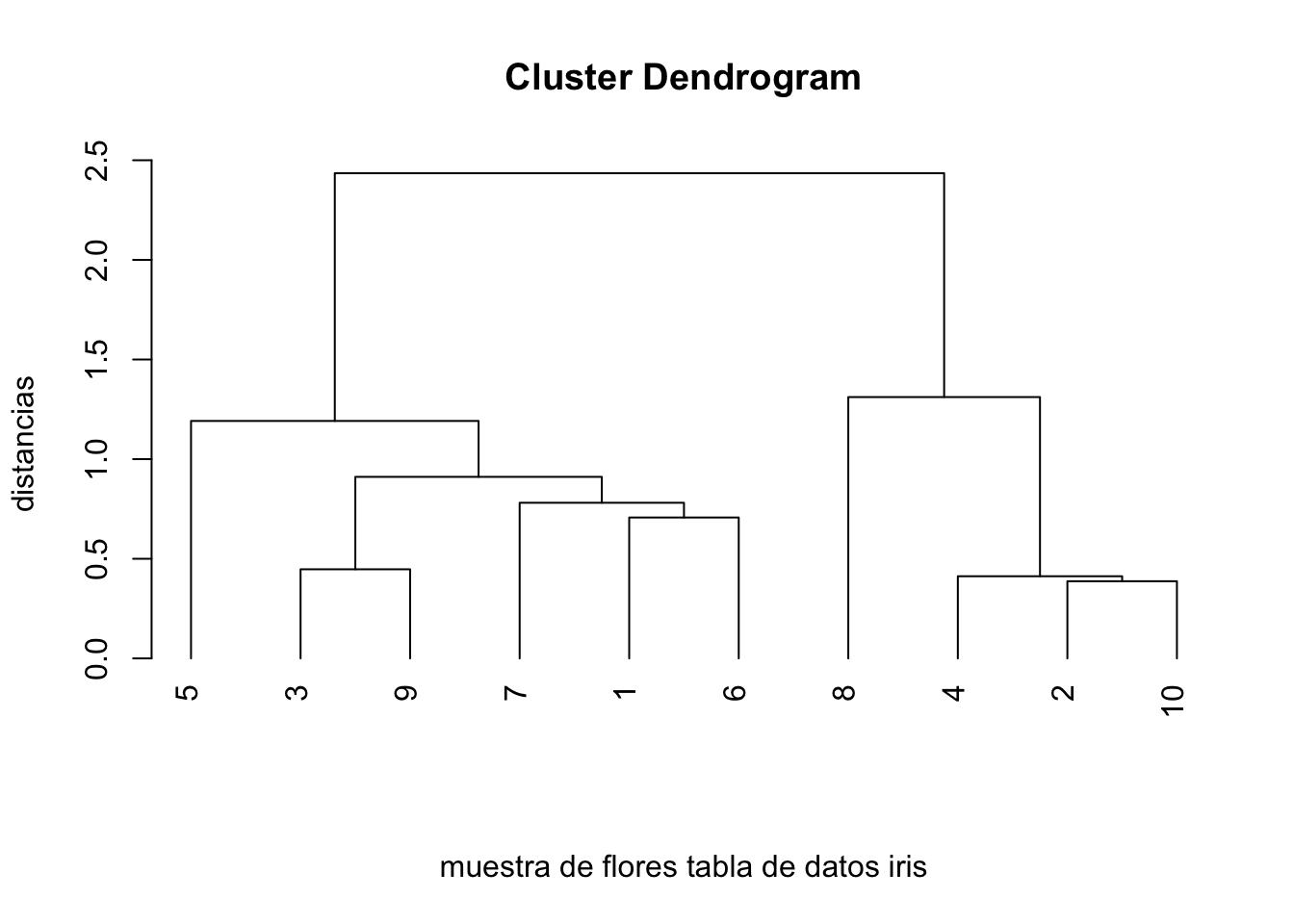
##  [9,]    7    8

R primero agrupa las flores 2 y 10 tal como hemos hecho anteriormente a mano.

Seguidamente agrupa la flor número 4 con el cluster creado en el paso 1 ($\{2,10\}$) creando el nuevo cluster $\{2,4,10\}$.

Seguidamente agrupa las flores 3 y 9 creando el cluster $\{3,9\}$.

Fijarse que los tres pasos coinciden con los pasos hechos a mano.

En el cuarto paso agrupa las flores 1 y 6 creando el cluster $\{1,6\}$.

En el quinto, la flor 7 con el cluster creado en el paso 4 ($\{1,6\}$) creando el cluster $\{1,6,7\}$.

En el sexto paso agrupa los clusters creados en el paso 3 $\{3,9\}$ y en el paso 5 $\{1,6,7\}$ creando el cluster $\{1,3,6,7,9\}$.

En el séptimo paso agrupa la flor número 5 con el cluster creado en el sexto paso ($\{1,3,6,7,9\}$) creando el cluster $\{1,3,5,6,7,9\}$.

En el octavo paso agrupa la flor número 8 con el cluster creado en el segundo paso ($\{2,10,4\}$) creando el cluster $\{2,4,8,10\}$.

Por último, en el noveno paso, agrupa los clusters creados en el paso 7 ($\{1,3,5,6,7,9\}$) y en el paso 8 ($\{2,4,8,10\}$) creando el cluster formado por todas las flores de la muestra.

Para ver a qué distancias ha realizado los agrupamientos, hacemos lo siguiente:

estudio.clustering.iris$height

## [1] 0.3873 0.4123 0.4472 0.7071 0.7810 0.9110 1.1916 1.3115 2.4352

Fijarse que las tres primeras distancias corresponden a las distancias con las que hemos creado los nuevos clusters en los tres primeros pasos realizados a mano.

9.3.8 Gráfico del árbol binario o dendrograma

La visualización de los pasos del clustering aglomerativo se realiza mediante un árbol binario denominado dendrograma.

Para visualizarlo en R basta usar la función plot:

plot(estudio.clustering,hang=...,labels=...)

donde

hang es un parámetro que controla la situación de las hojas del dendrograma respecto del margen inferior.
labels es un vector de caracteres que permite poner nombres a los objetos; por defecto, se identifican en la representación gráfica por medio de sus números de fila en la matriz o el data frame que contiene los datos.

Ejemplo de la muestra de flores iris

El dendrograma para estudio del clustering aglomerativo de los datos de la muestra de flores iris es el siguiente:

plot(estudio.clustering.iris,hang=-1,xlab="muestra de flores tabla de datos iris",
     sub="", ylab="distancias",labels=1:10)

Fijaos como los agrupamientos comentados anteriormente se visualizan en el dendrograma.

9.3.9 ¿Cómo calcular los clusters definidos por un clustering jerárquico?

Un clustering jerárquico puede usarse para definir un clustering ordinario, es decir, una clasificación de los objetos bajo estudio dando los clusters correspondientes.

Dichos clusters se pueden hallar de dos maneras: indicando cuántos clusters deseamos, o indicando a qué altura queremos cortar el dendrograma, de manera que clusters que se unan a una distancia mayor que dicha altura queden separados.

En el dendrograma del ejemplo anterior, si sólo queremos tres clusters, éstos deben ser: \[ \{1,3,5,6,7,9\},\ \{8\},\ \{2,4,10\}. \]

En cambio, si cortamos por una distancia de 1.5, sólo aparecerán dos clusters: \[ \{1,3,5,6,7,9\},\ \{2,4,8,10\}. \]

Para calcular los clusters en R debemos usar la función cutree:

cutree(estudio.clustering,k=...,h=...)

donde:

k es un parámetro que indica el número de clusters deseado
h es un parámetro que indica la altura a la que queremos cortar.

Ejemplo de la muestra de flores iris

En el ejemplo de la muestra de flores iris, si sólo queremos tres clusters para el estudio de clustering aglomerativo, hemos de hacer lo siguiente:

cutree(estudio.clustering.iris,k=3)

##  1  2  3  4  5  6  7  8  9 10 
##  1  2  1  2  1  1  1  3  1  2

Observamos que R nos ha dado los mismos clusters que hemos indicado anteriormente.

Si cortamos a una distancia de 1.5, los clusters serán:

cutree(estudio.clustering.iris,h=1.5)

##  1  2  3  4  5  6  7  8  9 10 
##  1  2  1  2  1  1  1  2  1  2

dando los mismos clusters vistos anteriormente.

Para visualizar los clusters en el dendrograma hemos de usar la función rect.hclust:

plot(estudio.clustering,...)
rect.hclust(estudio.clustering,h=...,k=...)

Fijarse que antes de llamar a la función rect.hclust hemos de realizar el dendrograma usando la función plot.

Ejemplo de la muestra de flores iris

Visualicemos los clusters anteriores:

plot(estudio.clustering.iris,hang=-1,xlab="muestra de flores tabla de datos iris",
     sub="", ylab="distancias",labels=1:10)
rect.hclust(estudio.clustering.iris,k=3)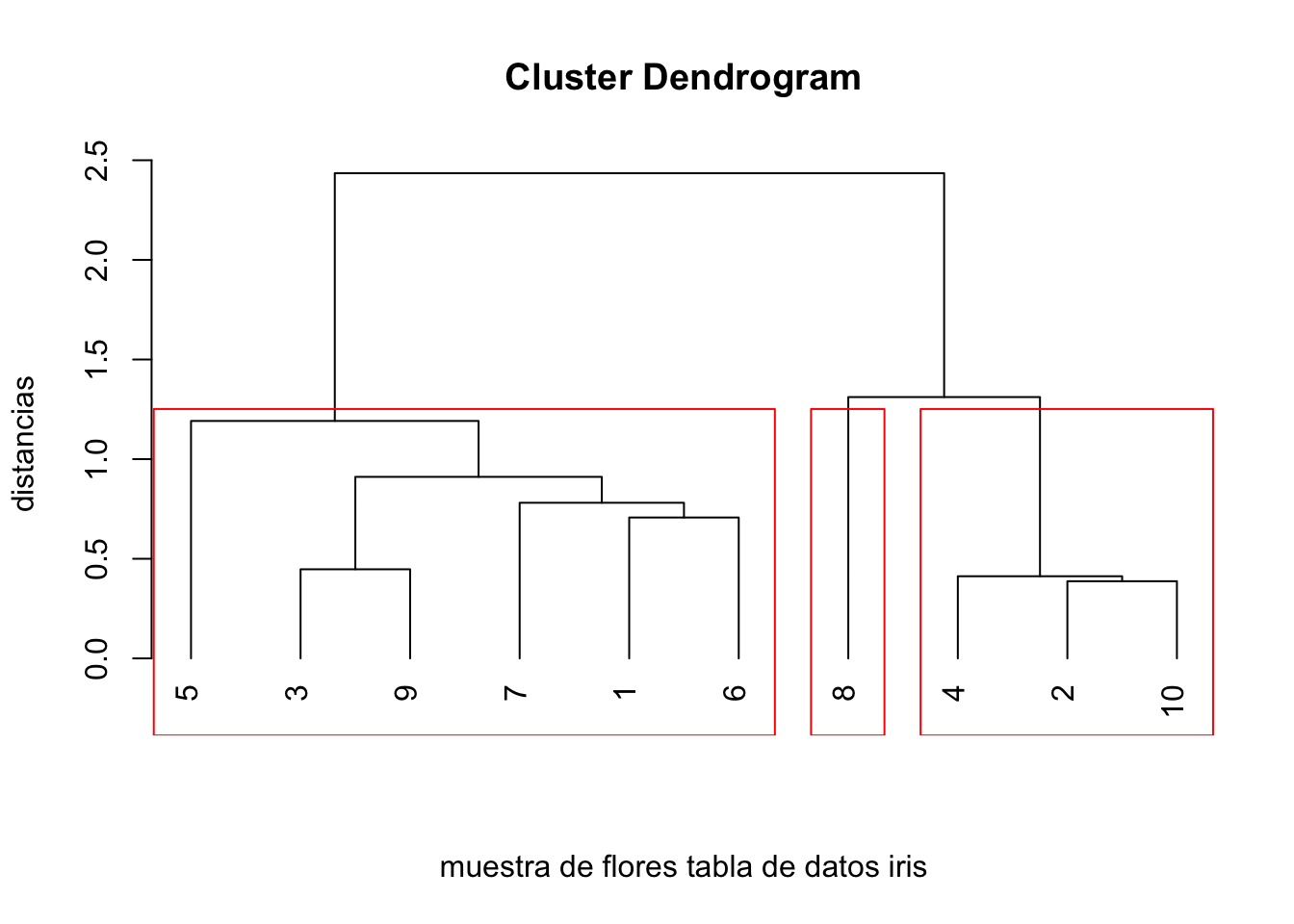

plot(estudio.clustering.iris,hang=-1,xlab="muestra de flores tabla de datos iris",
     sub="", ylab="distancias",labels=1:10)
rect.hclust(estudio.clustering.iris,h=1.5)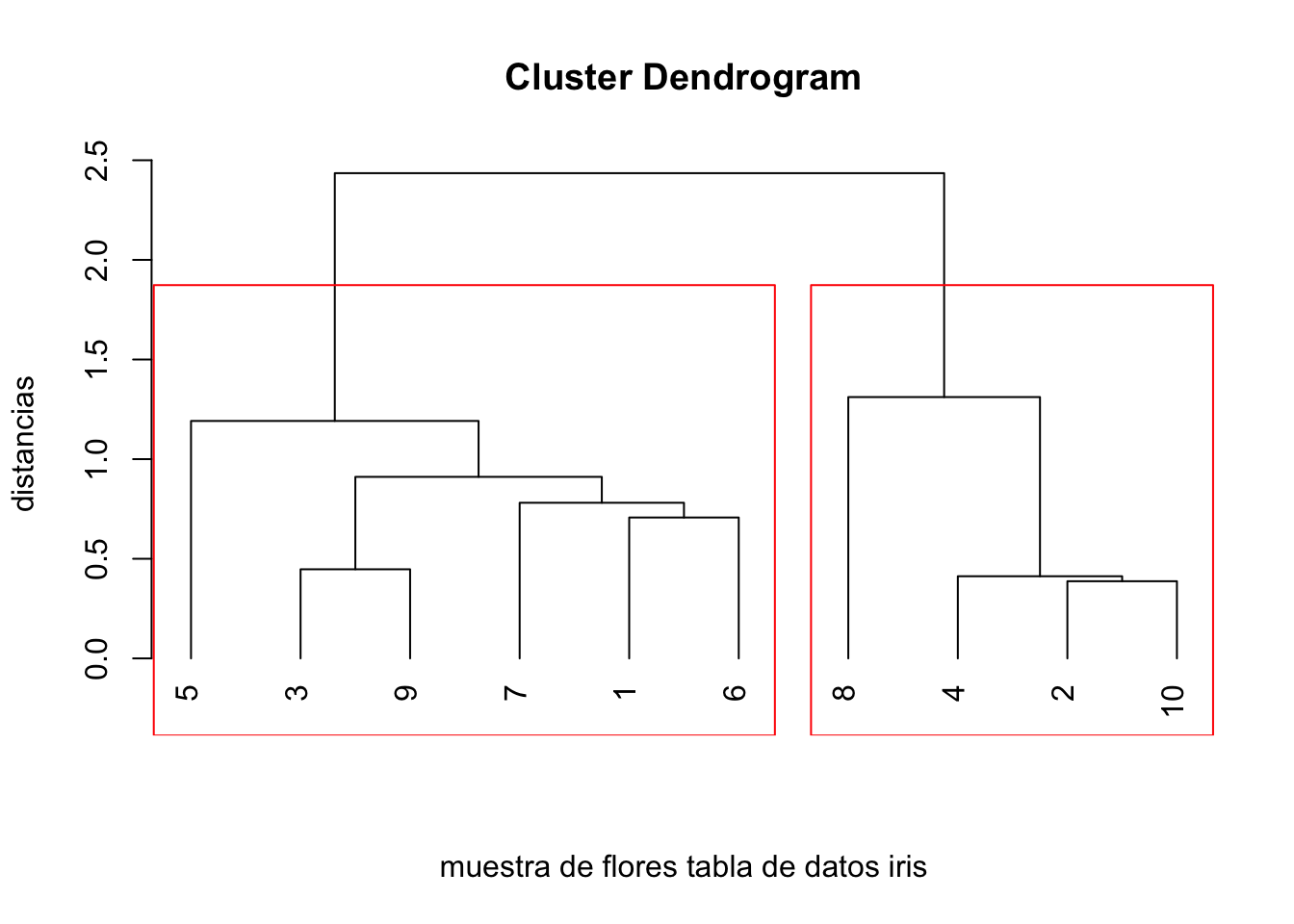

9.3.10 Propiedades de los métodos en el clustering jerárquico

Si usamos el método del enlace simple, donde recordemos que \[ d(C,C_1+C_2)=\min \left(d(C,C_1),d(C,C_2)\right), \] tiende a construir clusters grandes: clusters que tendrían que ser diferentes pero que tienen dos individuos próximos se unen en un único cluster.

Si usamos el método del enlace completo, donde recordemos que \[ d(C,C_1+C_2)=\max \left(d(C,C_1),d(C,C_2)\right), \] se comporta de forma totalmente diferente agrupando clusters solo cuando todos los puntos están próximos.

Si usamos el método de enlace promedio, donde recordemos que \[ d(C,C_1+C_2)=\frac{|C_1|}{|C_1|+ |C_2|} d(C,C_1)+\frac{|C_2|}{|C_1| + |C_2|} d(C,C_2), \] se comportaría como una solución intermedia entre los dos métodos anteriores.

Dicho método es muy usado en la reconstrucción de árboles filogenéticos a partir de matrices de distancias (método UPGMA, Unweighted Pair Group Method Using Arithmetic Averages)

Ejemplo de la muestra de flores iris

Si en lugar de usar el método del enlace simple usamos el método del enlace completo en la muestra de la tabla de datos de flores iris, obtenemos el dendrograma siguiente:

estudio.clustering.iris.completo=hclust(dist(tabla.iris[,1:4]),method="complete")
plot(estudio.clustering.iris.completo,hang=-1,xlab="muestra de flores tabla de datos iris",
     sub="", ylab="distancias",labels=1:10)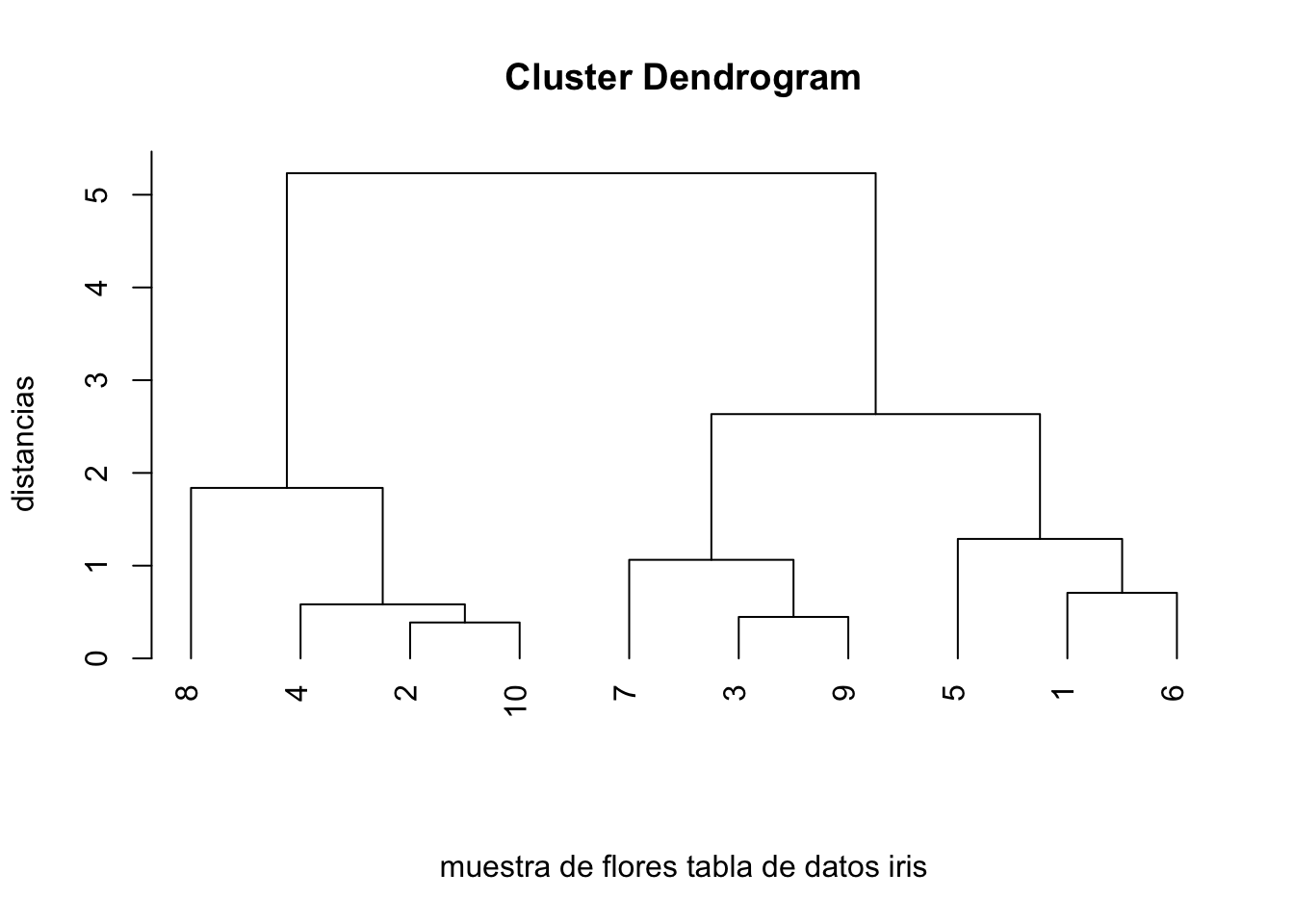

Si cortamos a la misma distancia que antes, h=1.5 obtenemos los clusters siguientes:

cutree(estudio.clustering.iris.completo,h=1.5)

##  1  2  3  4  5  6  7  8  9 10 
##  1  2  3  2  1  1  3  4  3  2

Observamos que ahora nos ha creado 4 clusters: \[ \{1,5,6\},\ \{2,4,10\},\ \{7,9\},\ \{8\}, \] comportándose tal como hemos indicado, es decir, “le cuesta” hacer clusters grandes.

Visualicemos el resultado:

plot(estudio.clustering.iris.completo,hang=-1,
     xlab="muestra de flores tabla de datos iris",
     sub="", ylab="distancias",labels=1:10)
rect.hclust(estudio.clustering.iris,h=1.5)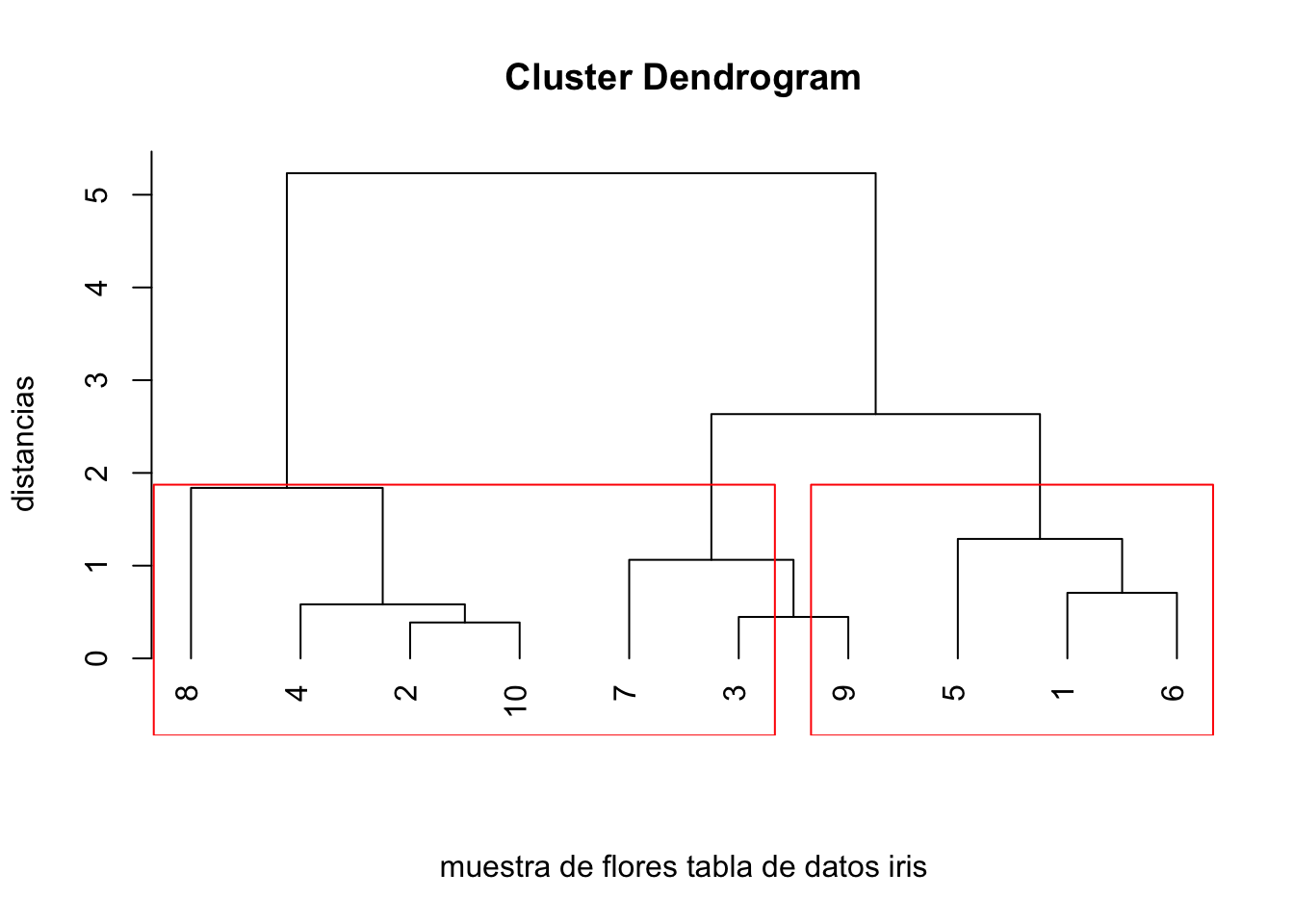

Ejemplo de los arrestados por posesión de cantidades pequeñas de marihuana

Realizemos el análisis de clustering aglomerativo usando el algoritmo de Ward para los datos binarios de este ejemplo.

Como la matriz de distancias es una matriz de similaridad y la matriz de distancias que tenemos que considerar es una matriz de disimilaridad al usar la función hclust, hacemos 1-matriz.dist.hamming para tener una matriz de disimilaridad.

Otra cosa a tener en cuenta es que la función hclust sólo admite objetos tipo dist, por tanto, tenemos que transformar la matriz de distancias en un objeto dist.

Sin más preámbulos, guardamos en el objeto estudio.clustering.arrestados el análisis del clustering jerárquico:

estudio.clustering.arrestados=hclust(as.dist(1-matriz.dist.hamming),method="ward.D")

La visualización de los resultados es la siguiente:

plot(estudio.clustering.arrestados,hang=-1,xlab="muestra de arrestados",
     sub="", ylab="distancias")

Observamos que, como hay muchas distancias con valores 0, tenemos 12 arrestados en un cluster inicial que se unen a distancia 0: $\{2,3,4,5,6,7,11,13,21,23,24,25\}.$ También se unen a dicha distancia los arrestados 20 y 22 en el cluster $\{20,22\}$, los arrestados 8 y 17 en el cluster $\{8,17\}$, los arrestados 1, 14 y 19 en el cluster $\{1,14,19\}$ y los arrestados 9, 10 y 15 en el cluster $\{9,10,15\}$.

A continuación a distancia $\frac{1}{3}$, se unen los clusters $\{18\}$, y $\{8,17\}$ en el cluster $\{8,17, 18\}$.

Después, a distancia 0.375, se unen los clusters $\{12\}$ y $\{1,14,19\}$ en el cluster $\{1,12,14,19\}$ y los clusters $\{16\}$ y $\{9, 10, 15\}$ en el cluster $\{9,10,15,16\}$.

El siguiente paso es la unión a distancia 0.7083333 de los clusters $\{20,22\}$ y $\{1,12,14,19\}$ en el cluster $\{1,12,14,19,20,22\}$.

El siguiente paso es la unión a distancia 1.25 de los clusters $\{8,17, 18\}$ y $\{1,12,14,19,20,22\}$ en el cluster $\{1,8,12,14,18,19,20,22\}$.

El penúltimo paso es la unión a distancia 1.59375 de los clusters $\{2,3,4,5,6,7,11,13,21,23,24,25\}$ y $\{9,10,15,16\}$ en el cluster $\{2,3,4,5,6,7,9,10,11,13,15,16,21,23,24,25\}$.

El último paso es la unión a distancia 2.6045833 de los clusters $\{1,8,12,14,18,19,20,22\}$ y $\{2,3,4,5,6,7,9,10,11,13,15,16,21,23,24,25\}$ en el cluster formado por todos los arrestados.

9.4 Guía rápida

kmeans(x, centers=..., iter.max=..., algorithm =...): aplica el algoritmo de $k$-medias a una tabla de datos, donde:
- x es la matriz o el data frame cuyas filas representan los objetos; en ambos casos, todas las variables han de ser numéricas como ya hemos indicado.
- centers sirve para especificar los centros iniciales, y se puede usar de dos maneras: igualado a un número $k$, R escoge aleatoriamente los $k$ centros iniciales, mientras que igualado a una matriz de $k$ filas y el mismo número de columnas que x, R toma las filas de esta matriz como centros de partida.
- iter.max permite especificar el número máximo de iteraciones a realizar; su valor por defecto es 10. Al llegar a este número máximo de iteraciones, si el algoritmo aún no ha acabado porque los clusters aún no hayan estabilizado, se para y da como resultado los clusters que se han obtenido en la última iteración.
- algorithm indica el algoritmo a usar. Los algoritmos pueden ser los siguientes: Hartigan-Wong, Lloyd, MacQueen.
Salida de kmeans (suponemos que hemos guardado en el objeto resultado.km la salida del algoritmo):
- resultado.km$size: nos da los números de objetos, es decir, los tamaños de cada cluster.
- resultado.km$cluster: nos dice qué cluster pertenece cada uno de los objetos de nuestra tabla de datos.
- resultado.km$centers: nos da los centros de cada cluster en filas. Es decir, la fila 1 sería el centro del cluster 1, la fila 2, del cluster 2 y así sucesivamente.
- resultado.km$withinss: nos da las sumas de cuadrados de cada cluster, lo que antes hemos denominado $SS_{C_j}$, para $j=1,\ldots,k$.
- resultado.km$tot.withinss: la suma de cuadrados de todos los clusters, lo que antes hemos denominado $SS_C$. También se puede calcular sumando las sumas de los cuadrados de cada cluster: sum(resultado.km$withinss).
- resultado.km$totss: es la suma de los cuadrados de las distancias de los puntos en su punto medio de todos estos puntos. Es decir, seria la suma de los cuadrados $SS_C$ pero suponiendo que sólo hubiera un sólo cluster.
- resultado.km$betweenss es la diferencia entre resultado.km$totss y resultado.km$tot.withinss y puede demostrarse (es un cálculo bastante tedioso) que es igual a la suma, ponderada por el número de objetos del cluster correspondiente, de los cuadrados de las distancias de los centros de los clusters al punto medio de todos los puntos.
dist(x, method=...): calcula la matriz de distancias de una tabla de datos, donde:
- x es nuestra tabla de datos (una matriz o un data frame de variables cuantitativas).
- method sirve para indicar la distancia que queremos usar, cuyo nombre se ha de entrar entrecomillado. La distancia por defecto es la euclídea que hemos venido usando hasta ahora. Otros posibles valores son (en lo que sigue, $\mathbf{x}=(x_1,\ldots,x_m)$ e $y=(y_1,\ldots,y_m)$ son dos vectores de $\mathbb{R}^m$):
- La distancia de Manhattan, manhattan, que recordemos que vale $\sum\limits_{i=1}^m |x_i-y_i|$.
- La distancia del máximo, maximum, que vale: $\max_{i=1,\ldots,m}|x_i-y_i|$.
- La distancia de Canberra, canberra, que vale $\sum\limits_{i=1}^m \frac{|x_i-y_i|}{|x_i|+|y_i|}$.
- La distancia de Minkowski, minkowski, que depende de un parámetro $p>0$ (que se ha de especificar en la función dist con p igual a su valor), y que vale: $\left(\sum_{i=1}^m |x_{i} - y_{i}|^p\right)^{1/p}$. Observad que cuando $p=1$ se obtiene la distancia de Manhattan y cuando $p=2$, la distancia euclídea usual.
- La distancia binaria, binary, que sirve básicamente para comparar vectores binarios (si los vectores no son binarios, R los entiende como binarios sustituyendo cada entrada diferente de 0 por 1). La distancia binaria entre x e y binarios es el número de posiciones en las que estos vectores tienen entradas diferentes, dividido por el número de posiciones en las que alguno de los dos vectores tiene un 1.

La salida de aplicar la función dist a nuestra tabla de datos es un objeto dist de R, no es una matriz de distancias usual.

scale(x, center = TRUE, scale = TRUE): escala los datos de una tabla de datos, donde:
- x: nuestra tabla de datos.
- center: es un parámetro lógico o un vector numérico de longitud el número de columnas de x indicando la cantidad que queremos restar a los valores de cada variable o columna. Si vale TRUE que es su valor por defecto, a cada columna se le resta la media de dicha columna.
- scale: es un parámetro lógico o un vector numérico de longitud el número de columnas de x indicando la cantidad por la que queremos dividir los valores de cada variable o columna. Si vale TRUE que es su valor por defecto, a los valores de cada columna se les divide por la desviación estándar de dicha columna.
hclust(d, method = ...): aplica el algoritmo de clustering aglomerativo a una tabla de datos, donde:
- d es la matriz de distancias entre nuestros objetos calculada con la función dist.
- method sirve para especificar cómo se define la distancia de la unión de dos clusters al resto de los clusters. El nombre del método se ha de entrar entrecomillado. Los más populares son los siguientes:
- Método de enlace completo, complete,
- Método de enlace simple, single,
- Método de enlace promedio, average,
- Método de la mediana, median,
- Método del centroide, centroid,
- Método de Ward clásico, ward.D.
Salida de hclust: imaginemos que hemos guardado en el objeto estudio.clustering la salida del algoritmo:
- estudio.clustering$merge nos indica cómo ha ido agrupando los clusters. Es una matriz de $n-1$ filas y 2 columnas, donde $n$ es el número de objetos. En esta matriz, los objetos originales se representan con números negativos, y los nuevos clusters con números positivos que indican el paso en el que se han creado.
- estudio.clustering$height es un vector que contiene las distancias a las que se han ido agrupando los pares de clusters.
- plot(estudio.clustering,hang=...,labels=...): dibuja el dendrograma o el árbol binario del clustering aglomerativo realizado, donde:
  - hang es un parámetro que controla la situación de las hojas del dendrograma respecto del margen inferior.
  - labels es un vector de caracteres que permite poner nombres a los objetos; por defecto, se identifican en la representación gráfica por medio de sus números de fila en la matriz o el data frame que contiene los datos.
- cutree(estudio.clustering,k=...,h=...): calcula los clusters del clustering aglomerativo realizado, donde:
  - k es un parámetro que indica el número de clusters deseado
  - h es un parámetro que indica la altura a la que queremos cortar.
rect.hclust(estudio.clustering,h=...,k=...): dibuja los clusters hallados en el algoritmo de clustering aglomerativo realizado según el valor del parámetro h o el parámetro k. Antes de llamar a esta función, se tiene que haber llamado a la función plot para dibujar el dendrograma. En caso contrario, R da error.

Individuos/Variables	\(X_1\)	\(X_2\)	\(\ldots\)	\(X_m\)
1	\(x_{11}\)	\(x_{12}\)	\(\ldots\)	\(x_{1m}\)
2	\(x_{21}\)	\(x_{22}\)	\(\ldots\)	\(x_{2m}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(i\)	\(x_{i1}\)	\(x_{i2}\)	\(\ldots\)	\(x_{im}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(n\)	\(x_{n1}\)	\(x_{n2}\)	\(\ldots\)	\(x_{nm}\)

Nombre	\(\delta\)	\(\lambda\)	\(\alpha\)	\(\beta\)	Definición
Hamming	\(1\)	\(1\)	1	1	\(\dfrac{a_1 + a_0}{a_0+a_1+a_2}\)
Jaccard	\(0\)	\(1\)	1	0	\(\dfrac{a_1}{a_1 + a_2}\)
Tanimoto	\(1\)	\(2\)	1	1	\(\dfrac{a_1+a_0}{a_1+2a_2+a_0}\)
Rusell–Rao	0	1	1	1	\(\dfrac{a_1}{a_0+a_1+a_2}\)
Dice	\(0\)	\(0.5\)	1	0	\(\dfrac{2a_1}{2a_1 + a_2}\)
Kulczynski	0	1	0	0	\(\dfrac{a_1}{a_2}\)

Nombre	\(\delta_1\)	\(\delta_2\)	\(\delta_3\)	\(\delta_0\)
Enlace simple	\(1/2\)	\(1/2\)	\(0\)	\(-1/2\)
Enlace completo	\(1/2\)	\(1/2\)	\(0\)	\(1/2\)
Enlace promedio	\(\frac{\|C_1\|}{\|C_1\| + \|C_2\|}\)	\(\frac{\|C_2\|}{\|C_1\|+ \|C_2\|}\)	\(0\)	\(0\)
Centroide	\(\frac{\|C_1\|}{\|C_1\| + \|C_2\|}\)	\(\frac{\|C_2\|}{\|C_1\| + \|C_2\|}\)	\(-\frac{\|C_1\| \|C_2\|}{(\|C_1\| + \|C_2\|)^2}\)	\(0\)
Mediana	\(1/2\)	\(1/2\)	\(-1/4\)	\(0\)
Ward	\(\frac{\|C\| + \|C_1\|}{\|C\| + \|C_1\| + \|C_2\|}\)	\(\frac{\|C\| + \|C_2\|}{\|C\| + \|C_1\|+ \|C_2\|}\)	\(-\frac{\|C\|}{\|C\| + \|C_1\| + \|C_2\|}\)	\(0\)

Curso completo de Estadística Inferencial con R y Python

Tema 9 Introducción al Clustering

9.1 ¿Qué es el clustering?

9.1.1 Principios básicos

9.1.2 Tipos de algoritmos de clustering

9.2 Métodos de partición

9.2.1 Algoritmo de las \(k\)-medias (\(k\)-means)

9.2.2 Limitación del algoritmo de \(k\)-medias

9.2.3 Métodos para hallar el número de clusters \(k\). Método del codo

9.2.4 Algoritmo de \(k\)-medias con `R`

9.3 Clustering jerárquico

9.3.1 Distancias

9.3.2 Datos binarios

9.3.3 Datos continuos

9.3.4 Cálculo de distancias en `R`

9.3.5 Escalado de los datos

9.3.6 Clustering jerárquico aglomerativo

9.3.7 Clustering jerárquico aglomerativo con `R`

9.3.8 Gráfico del árbol binario o dendrograma

9.3.9 ¿Cómo calcular los clusters definidos por un clustering jerárquico?

9.3.10 Propiedades de los métodos en el clustering jerárquico

9.4 Guía rápida

Tema 9 Introducción al Clustering

9.1 ¿Qué es el clustering?

9.1.1 Principios básicos

9.1.2 Tipos de algoritmos de clustering

9.2 Métodos de partición

9.2.1 Algoritmo de las \(k\)-medias (\(k\)-means)

9.2.2 Limitación del algoritmo de \(k\)-medias

9.2.3 Métodos para hallar el número de clusters \(k\). Método del codo

9.2.4 Algoritmo de \(k\)-medias con R

9.3 Clustering jerárquico

9.3.1 Distancias

9.3.2 Datos binarios

9.3.3 Datos continuos

9.3.4 Cálculo de distancias en R

9.3.5 Escalado de los datos

9.3.6 Clustering jerárquico aglomerativo

9.3.7 Clustering jerárquico aglomerativo con R

9.3.8 Gráfico del árbol binario o dendrograma

9.3.9 ¿Cómo calcular los clusters definidos por un clustering jerárquico?

9.3.10 Propiedades de los métodos en el clustering jerárquico

9.4 Guía rápida

9.2.4 Algoritmo de \(k\)-medias con `R`

9.3.4 Cálculo de distancias en `R`

9.3.7 Clustering jerárquico aglomerativo con `R`