Tema 5 Bondad de Ajuste
En el capítulo anterior hemos visto toda una batería de contrastes de hipótesis basados en parámetros de poblaciones como por ejemplo \(\mu\), media de la población, \(p\), proporción de éxitos de la población, \(\sigma\), desviación típica de la población, etc.
En este tipo de contrastes, suponemos que conocemos el tipo de distribución de la población. O sea, sabemos que la variable \(X\), que nos da los valores de la población, es normal, binomial, o de otro tipo. Lo que no conocemos, y ésta es la razón de por qué realizamos este tipo de contrastes, es uno o más parámetros de los que depende la distribución de la variable \(X\).
Por ejemplo, si suponemos que \(X\) es normal y hacemos contrastes de hipótesis sobre su media, tenemos, por un lado, el caso en que conocemos la desviación típica \(\sigma\) y el caso en que no la conocemos.
A todo este tipo de contrastes se les conoce como contrastes paramétricos.
Ahora bien, suponer de qué tipo es la distribución de la variable \(X\) que nos da los valores de la población es de hecho “un brindis al sol”. ¿En qué nos basamos en decir que la distribución de \(X\) es normal por ejemplo? ¿Qué evidencias basadas en información sobre los valores de una muestra de dicha población tenemos de la normalidad de \(X\)?
Este tipo de preguntas son las que intentan responder los contrastes no paramétricos. Son contrastes en los que la hipótesis nula no consiste en averiguar si un determinado parámetro vale un cierto valor sino que la distribución de la variable \(X\) es de un tipo u otro. Una vez que tengamos evidencias suficientes de la normalidad de \(X\), podemos pasar a una “segunda fase” e intentar saber alguna información sobre los parámetros de los que depende la distribución de \(X\) usando los contrastes paramétricos.
5.1 Contrastes de bondad de ajuste
Uno de las técnicas más conocidas para estudiar los contrastes no paramétricos son los tests de bondad de ajuste o tests \(\chi^2\).
El contraste que intentamos estudiar es del tipo siguiente: \[ \left. \begin{array}{ll} H_0: \mbox{ La distribución de $X$ es del tipo $X_0$,}\\ H_1: \mbox{ La distribución de $X$ no es del tipo $X_0$,} \end{array} \right\} \] donde \(X_0\) es un tipo de distribución conocida.
5.1.1 Pruebas gráficas: histogramas
Supongamos que nuestra variable \(X_0\) es continua.
Para comprobar si una determinada muestra proviene de la variable \(X_0\), lo primero que podemos hacer es realizar distintas pruebas gráficas como por ejemplo histogramas.
A partir de dichos histogramas, podemos “estimar” la función de densidad de la muestra y ver si dicha función de densidad se parece o no a la función de densidad de la variable \(X_0\).
La estimación de la función de densidad a partir del histograma de la muestra se sale de los objetivos del curso pero vamos a ver con un ejemplo cómo podemos usar dicha función. Si queréis detalles, consultad https://en.wikipedia.org/wiki/Kernel_density_estimation.
Ejemplo
Consideremos la tabla de datos iris, concretamente la variable anchura del sépalo (Sepal.Width).
Queremos ver a qué se puede aproximar dicha variable.
Vamos a realizar un gráfico de la estimación de la función de densidad de la muestra usando la función density de R:

A “ojo de buen cubero”, parece una campana de Gauss. Para comprobarlo, dibujemos además la función de densidad de la distribución normal con parámetros \(\mu\) igualado a la media de la muestra y \(\sigma\), a la desviación típica:
muestra=iris$Sepal.Width
plot(density(muestra),main="Estimación de la densidad")
x=seq(from=1,to=5,by=0.01)
mu=mean(iris$Sepal.Width)
sigma=sd(iris$Sepal.Width)
lines(x,dnorm(x,mean=mu,sd=sigma),col="red")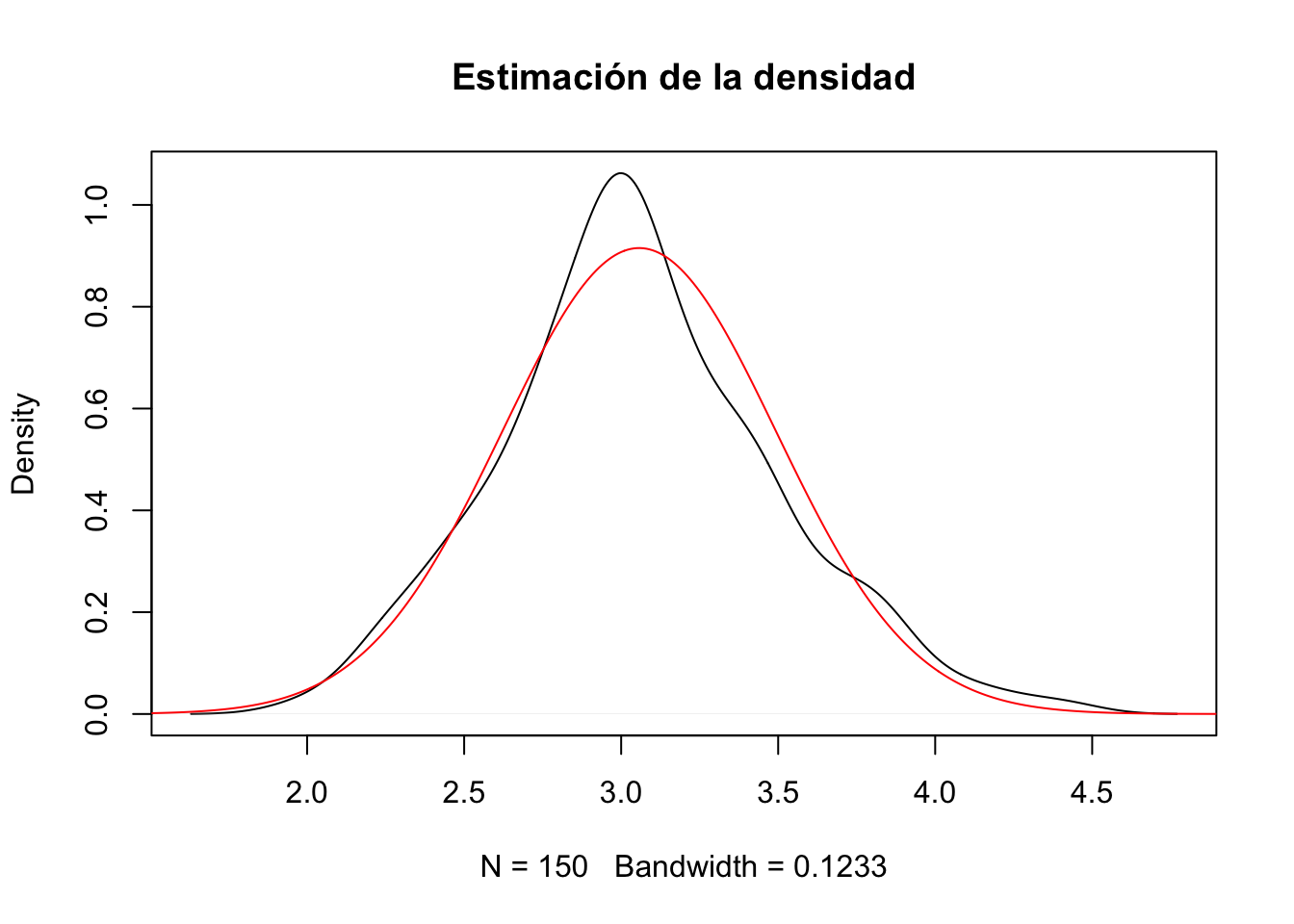
Vemos que la campana de Gauss se parece bastante a la estimación de la densidad.
La cuestión ahora es: ¿podemos aceptar que el parecido es suficiente para aceptar que la distribución de la anchura del sépalo es normal?
La respuesta será contestada en secciones posteriores.
5.1.2 Pruebas gráficas: Q-Q-plots
Otro tipo de prueba gráfica que podemos realizar son los llamados gráficos cuantil-cuantil o Q-Q-plots.
Este tipo de gráficos compara los cuantiles observados de la muestra con los cuantiles teóricos de la distribución teórica.
La función de R que realiza un gráfico de este tipo es la función qqPlot del paquete car.
Su sintaxis básica es
donde:
xes el vector con la muestra.El parámetro
distributionse ha de igualar al nombre de la familia de distribuciones entre comillas, y puede tomar como valor cualquier familia de distribuciones de la que R sepa calcular la densidad y los cuantiles: esto incluye las distribuciones que hemos estudiado hasta el momento:"norm","binom","poisson","t", etc.A continuación, se tienen que entrar los parámetros de la distribución, igualando su nombre habitual (
meanpara la media,sdpara la desviación típica,dfpara los grados de libertad, etc.) a su valor.Por defecto, el gráfico obtenido con la función
qqPlotidentifica los dos Q-Q-puntos con ordenadas más extremas. Para omitirlos, usad el parámetroid=FALSE.
Otros parámetros a tener en cuenta:
qqPlotañade por defecto una rejilla al gráfico, que podéis eliminar congrid=FALSE.qqPlotañade por defecto una línea recta que une los Q-Q-puntos correspondientes al primer y tercer cuartil: se la llama recta cuartil-cuartil. Un buen ajuste de los Q-Q-puntos a esta recta significa que la muestra se ajusta a la distribución teórica, pero posiblemente con parámetros diferentes a los especificados. Os recomendamos mantenerla, pero si queréis eliminarla por ejemplo para substituirla por la diagonal \(y=x\), podéis usar el parámetroline="none".qqPlottambién añade dos curvas discontinuas que abrazan una “región de confianza del 95%” para el Q-Q-plot. Sin entrar en detalles, esta región contendría todos los Q-Q-puntos en un 95% de las ocasiones que tomáramos una muestra de la distribución teórica del mismo tamaño que la nuestra. Por lo tanto, si todos los Q-Q-puntos caen dentro de esta franja, no hay evidencia para rechazar que la muestra provenga de la distribución teórica. Esta franja de confianza es muy útil para interpretar el Q-Q-plot, pero la podéis eliminar conenvelope=FALSE.Se pueden usar los parámetros usuales de
plotpara poner nombres a los ejes, título, modificar el estilo de los puntos, etc., y otros parámetros específicos para modificar el aspecto del gráfico. Por ejemplo,col.linessirve para especificar el color de las líneas que añade.
Hagamos un gráfico Q-Q-plot del ejemplo anterior.
Ejemplo
Recordemos que considerábamos la variable anchura del sépalo de la tabla de datos iris.
El Q-Q-plot para ver si la variable anterior sigue la ley normal es el siguiente:
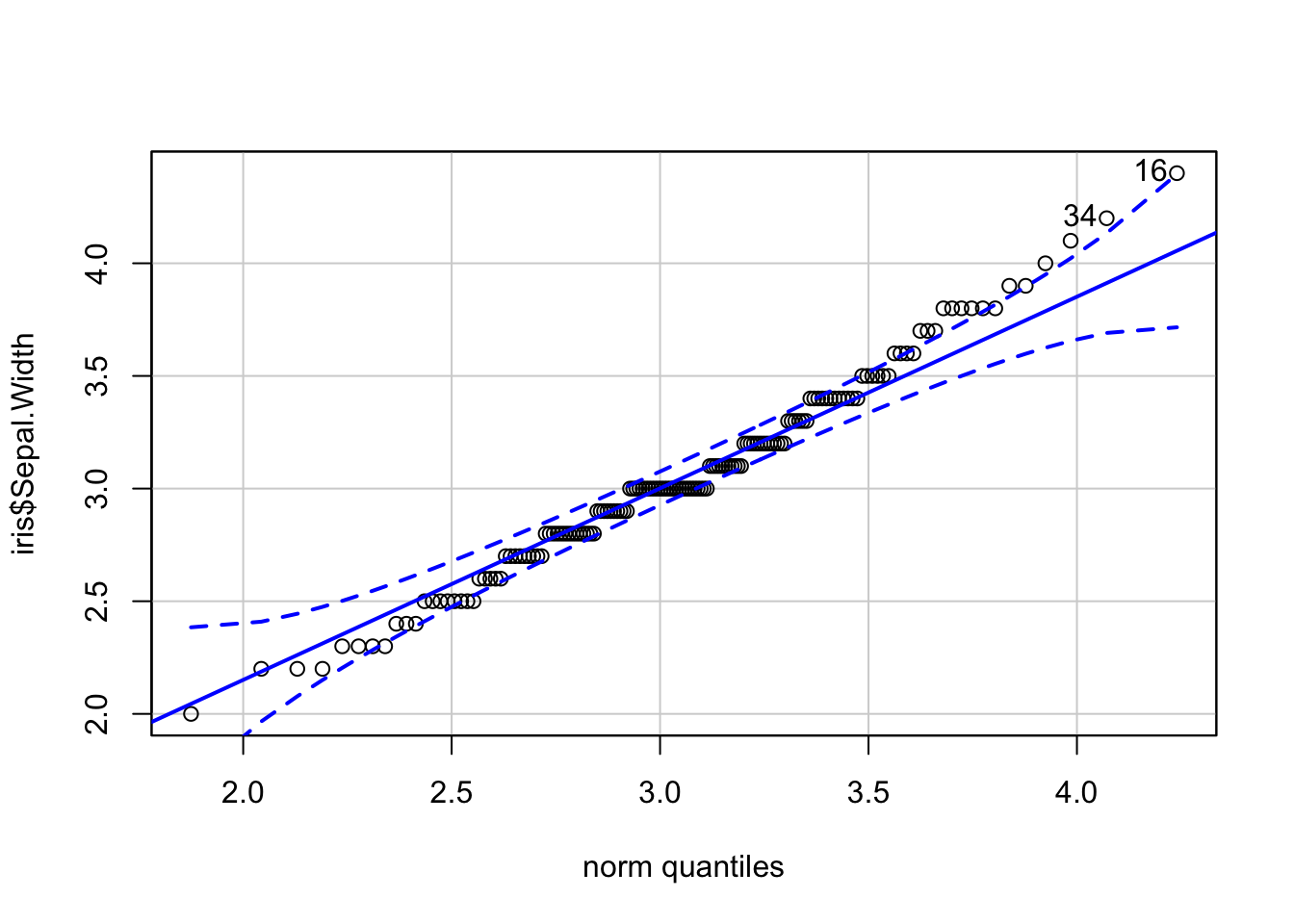
## [1] 16 34Observamos que la mayoría de los valores de la muestra caen dentro de la franja del 95% de confianza.
Sin embargo, fijáos que hay unos pocos puntos que se salen de dicha franja.
En resumen, según esta prueba gráfica, “parece” que la distribución es normal pero tenemos dudas.
5.1.3 Contraste \(\chi^2\) de Pearson
Veamos a continuación cómo se realiza un contraste \(\chi^2\) de Pearson.
Suponemos que disponemos de los valores de una muestra de tamaño \(n\) de la variable \(X\) que nos da los valores de la población: \(x_1,x_2,\ldots,x_n\).
A continuación, clasificamos los valores \(x_i\), \(i=1,\ldots, n\) en \(k\) clases. La elección de estas clases depende del problema estudiado y del contexto del mismo.
Sean \(n_1,\ldots,n_k\), el número de valores de la muestra que están en cada una de las clases: \(n_1\) sería el número de valores de la muestra que están en la clase 1, \(n_2\), el número de valores de la muestra que están en la clase 2 y así sucesivamente hasta \(n_k\).
Obtendríamos lo que se conoce como tabla de frecuencias empíricas:
| Clases | Clase 1 | Clase 2 | \(\ldots\) | Clase \(k\) | Total |
|---|---|---|---|---|---|
| Frecuencias empíricas | \(n_1\) | \(n_2\) | \(\ldots\) | \(n_k\) | \(n\) |
El siguiente paso es obtener la tabla de la función de probabilidad de la variable discreta \(X_k\) de valores \(\{1,\ldots,k\}\) y con función de probabilidad \(p_i=P(X_k=i)=P(X_0\in\mbox{Clase i})\), \(i=1,\ldots,k\).
Esta función de probabilidad tiene que hallarse a partir del conocimiento de \(X_0\). Si desconocemos alguno(s) del (de los) parámetro(s) de (los) que depende \(X_0\), los tendremos que estimar usando las técnicas vistas en el capítulo de estimación de parámetros.
La tabla de la función de probabilidad \(X_k\) quedaría de la forma siguiente:| \(X_k\) | \(1\) | \(2\) | \(\ldots\) | \(k\) | Total |
|---|---|---|---|---|---|
| \(P(X_k=i)\) | \(P(X_k=1)\) | \(P(X_k=2)\) | \(\ldots\) | \(P(X_k=k)\) | \(1\) |
| Clases | Clase 1 | Clase 2 | \(\ldots\) | Clase \(k\) | Total |
|---|---|---|---|---|---|
| Frecuencias teóricas | \(n\cdot P(X_k=1)\) | \(n\cdot P(X_k=2)\) | \(\ldots\) | \(n\cdot P(X_k=k)\) | \(n\) |
| Frecuencias teóricas | \(e_1\) | \(e_2\) | \(\ldots\) | \(e_k\) | \(n\) |
Llamaremos \(e_i=n\cdot P(X_k=i)\) a la frecuencia teórica de la clase \(i\)-ésima. (\(e\) de “esperada”)
El test \(\chi^2\) o test de bondad de ajuste se basa en que, si la hipótesis nula es cierta, las frecuencias empíricas y las frecuencias teóricas son “parecidas”.
Más concretamente, si la hipótesis nula es cierta, el estadístico siguiente: \[ \chi^2 = \sum_{i=1}^k \frac{(\mbox{frec. empíricas}_i-\mbox{frec. teóricas}_i)^2}{\mbox{frec. teóricas}_i}= \sum_{i=1}^k \frac{(n_i-e_i)^2}{e_i}, \] sigue aproximadamente al distribución \(\chi^2_{k-1}\) grados de libertad.
Sea \(\chi_0\) el valor del estadístico de contraste anterior para nuestra muestra. El p-valor del contraste vale: \[ p=P(\chi_{k-1}^2 > \chi_0), \]
con el significado usual:
- si \(p<0.05\), concluimos que tenemos evidencias suficientes para rechazar la independencia de los criterios,
- si \(p>0.1\), concluimos que no tenemos evidencias suficientes para rechazar la independencia de los criterios y,
- si \(0.05\leq p\leq 0.1\), estamos en la zona de penumbra. Necesitamos más datos para tomar una decisión clara.
Ejemplo del lanzamiento de un dado
Imaginemos que queremos ver si un dado está trucado o no.
Si no está trucado, cuando tiramos el dado y miramos el resultado \(X\), cada resultado \(i=1,\ldots,6\) tiene probabilidad \(P(X=i)=\frac{1}{6}\). Ésta sería, por tanto, la función de distribución de la variable \(X_k\).
Las clases serían posibles valores que puede tener el dado al lanzarse. La distribución de la variable \(X_k\) sería en este caso:
| \(X_k\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | Total |
|---|---|---|---|---|---|---|---|
| \(P(X_k=i)\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(1\) |
Nos dicen que han lanzado el dado 120 veces y se han obtenido los resultados siguientes:
| Clases | Clase 1 | Clase 2 | Clase 3 | Clase 4 | Clase 5 | Clase 6 | Total |
|---|---|---|---|---|---|---|---|
| Frecuencias empíricas | 20 | 22 | 17 | 18 | 19 | 24 | 120 |
¿Hay bastante evidencia que el dado esté trucado?
Resolución
La tabla de frecuencias teóricas sería:
| Clases | Clase 1 | Clase 2 | Clase 3 | Clase 4 | Clase 5 | Clase 6 | Total |
|---|---|---|---|---|---|---|---|
| Frecuencias teóricas | \(\frac{120}{6}=20\) | \(\frac{120}{6}=20\) | \(\frac{120}{6}=20\) | \(\frac{120}{6}=20\) | \(\frac{120}{6}=20\) | \(\frac{120}{6}=20\) | \(120\) |
El valor del estadístico \(\chi^2\) sería: \[ \begin{array}{rl} \chi_0 = &\frac{(20-20)^2}{20}+\frac{(22-20)^2}{20}+\frac{(17-20)^2}{20}+\frac{(18-20)^2}{20}\\ & +\frac{(19-20)^2}{20}+\frac{(24-20)^2}{20} = 1.7. \end{array} \]
El p-valor del contraste sería \(P(\chi_5^2 > 1.7)\):
## [1] 0.8889Como el p-valor es grande, concluímos que no tenemos evidencias suficientes para rechazar que el dado esté trucado.
5.1.4 Condiciones para poder aplicar el test \(\chi^2\) de Pearson
El test de bondad de ajuste está basado en el estadístico \(\chi^2\) que recordemos sigue aproximadamente una distribución \(\chi^2_{k-1}\) grados de libertad.
Al estar basado en un Teorema Límite, para que dicha aproximación sea efectiva, las condiciones siguientes se tienen que verificar:
el tamaño de la muestra tiene que ser grande: \(n\geq 25\) o mejor \(n\geq 30\),
las clases tienen que cubrir todos los resultados posibles, (en la práctica: \(n=\sum_{i=1}^k n_i = \sum_{i=1}^k e_i\))
las frecuencias teóricas tienen que ser mayores o iguales que 5: \(e_i\geq 5\), para todo \(i=1,\ldots,k\).
Ejemplo del lanzamiento de un dado
En el ejemplo del lanzamiento del dado, observamos que se verifican las condiciones anteriores:
- \(n=120\geq 30\),
- \(\begin{array}{rl} \displaystyle\sum_{i=1}^6 n_i =& 20+22+17+18+19+24=120\\ = & \sum_{i=1}^6 e_i =20+20+20+20+20+20 \end{array},\)
- \(e_1=e_2=e_3=e_4=e_5=e_6=20\geq 5.\)
5.1.5 Resolución de un test \(\chi^2\) de Pearson en R
Para resolver un contraste de bondad de ajuste en R, hemos de usar la función chisq.test.
Su sintaxis básica es
donde:
xes el vector (o la tabla, calculada contable) de frecuencias absolutas observadas de las clases en la muestra, recordemos que las hemos llamado \(n_i\), \(i=1,\ldots, k\).pes el vector de probabilidades teóricas de las clases para la distribución que queremos contrastar. O sea, es el vector de la función de probabilidad de la variable \(X_k\): \(p_i=P(X_k=i)\), \(i=1,\ldots k\).
Si no lo especificamos, se entiende que la probabilidad es la misma para todas las clases. Obviamente, estas probabilidades se tienen que especificar en el mismo orden que las frecuencias de x y, como son las probabilidades de todos los resultados posibles, en principio tienen que sumar 1; esta condición se puede relajar con el siguiente parámetro.
rescale.pes un parámetro lógico que, si se iguala aTRUE, indica que los valores depno son probabilidades, sino solo proporcionales a las probabilidades; esto hace queRtome como probabilidades teóricas los valores deppartidos por su suma, para que sumen 1.
Por defecto vale FALSE, es decir, se supone que el vector que se entra como p son probabilidades y por lo tanto debe sumar 1, y si esto no pasa se genera un mensaje de error indicándolo. Igualarlo a TRUE puede ser útil, porque nos permite especificar las probabilidades mediante las frecuencias esperadas o mediante porcentajes. Pero también es peligroso, porque si nos hemos equivocado y hemos entrado un vector en p que no corresponda a una probabilidad, R no nos avisará.
simulate.p.valuees un parámetro lógico que indica a la función si debe optar por una simulación para el cálculo del p-valor del contraste.
Por defecto vale FALSE, en cuyo caso este p-valor no se simula sino que se calcula mediante la distribución \(\chi^2\) correspondiente.
Si falla una o más condiciones para que se aplique el test de bondad de ajuste, tendremos que especificarlo como TRUE y R realizará una serie de replicaciones aleatorias de la situación teórica: por defecto, 2000, pero su número se puede especificar mediante el parámetro B. Es decir, generará un conjunto de vectores aleatorios de frecuencias con la distribución que queremos contrastar, cada uno de suma total la de x. A continuación, calculará la proporción de estas repeticiones en las que el estadístico de contraste es mayor o igual que el obtenido para x, y éste será el p-valor que dará.
Ejemplo de la tabla de datos iris
Consideremos la tabla de datos iris. Imaginemos que queremos ver si en una muestra de tamaño 10, hay la misma cantidad de flores de las tres especies: setosa, versicolor y virgínica.
En primer lugar, elegimos una muestra de 10 flores:
A continuación, realizamos el contraste de bondad de ajuste:
##
## Chi-squared test for given probabilities
##
## data: table(muestra.flores)
## X-squared = 0.8, df = 2, p-value = 0.7Fijaos que R nos avisa que las aproximaciones pueden ser incorrectas. La razón es que las frecuencias observadas no son mayores que 5 ya que éstas valen: \(e_{setosa}=e_{versicolor}=e_{virginica}=\frac{10}{3}\approx 3.333.\)
Para solventar este problema, vamos a simular el p-valor:
##
## Chi-squared test for given probabilities with simulated p-value (based
## on 2000 replicates)
##
## data: table(muestra.flores)
## X-squared = 0.8, df = NA, p-value = 0.8Vemos que con 2000 replicaciones, al obtener un p-valor grande, podemos concluir que no tenemos evidencias suficientes para rechazar que la proporción de especies en la muestra no sea la misma.
Ejemplo para comprobar si cierta distribución es normal usando el test \(\chi^2\) de Pearson en R
Un técnico de medio ambiente quiere estudiar el aumento de temperatura del agua a dos kilómetros de los vertidos de agua autorizados de una planta industrial.
El responsable de la empresa afirma que estos aumentos de temperatura siguen una ley normal con \(\mu=3.5\) décimas de grado C y \(\sigma=0.7\) décimas de grado C.
El técnico lo posa en entredicho. Para decidirlo, toma una muestra aleatoria de 40 observaciones del aumento de las temperaturas (en décimas de grado) y se obtienen los resultados siguientes:
| Rango de temperaturas | Frecuencias |
|---|---|
| 1.45-1.95 | 2 |
| 1.95-2.45 | 1 |
| 2.45-2.95 | 4 |
| 2.95-3.45 | 15 |
| 3.45-3.95 | 10 |
| 3.95-4.45 | 5 |
| 4.45-4.95 | 3 |
¿Hay evidencia que la sospecha del técnico sea verdadera?
El contraste a realizar es el siguiente: \[\left\{ \begin{array}{l} H_0:\mbox{La distribución de los aumentos de temperatura es $N(3.5,0.7)$,}\\[1ex] H_1: \mbox{La distribución de los aumentos de temperatura no es $N(3.5,0.7)$.} \end{array} \right.\]
Para poder aplicar el test \(\chi^2\) de Pearson, como la distribución teórica es normal y su dominio es todo \(\mathbb{R}\), tendremos que ampliar los intervalos de la tabla anterior para asegurarnos que los valores de la tabla pueden alcanzar todos los valores de la distribución teórica:
| Rango de temperaturas | Frecuencias |
|---|---|
| \((-\infty,1.95]\) | 2 |
| \((1.95,2.45]\) | 1 |
| \((2.45,2.95]\) | 4 |
| \((2.95,3.45]\) | 15 |
| \((3.45,3.95]\) | 10 |
| \((3.95,4.45]\) | 5 |
| \((4.45,\infty)\) | 3 |
La tabla anterior nos determina las clases a considerar que corresponderían a los intervalos. Las frecuencias empíricas serían las que nos da la segunda columna de la tabla.
A continuación, vamos a calcular las frecuencias teóricas. Para ello, en primer lugar, hay que hallar la función de probabilidad de la variable \(X_k\):
Cálculo de \(p_1 = P(X_0\in \mbox{Clase }1)\): \[\scriptsize p_1 = P(X_0\leq 1.95)=P\left(Z\leq \frac{1.95-3.5}{0.7}\right)=P(Z\leq -2.214)=0.013, \] donde \(Z=N(0,1)\). Por tanto, \(e_1 = n\cdot 0.013=40\cdot 0.013=0.54.\)
Cálculo de \(p_2 = P(X_0\in \mbox{Clase }2)\): \[\scriptsize \begin{array}{rl} p_2 & = P(1.95 < X_0\leq 2.45)=P\left(\frac{1.95-3.5}{0.7} < Z \leq \frac{2.45-3.5}{0.7}\right) =P(-2.214 < Z\leq -1.5) \\ & =P(Z\leq -1.5)-P(Z\leq -2.214)=0.067-0.013=0.053. \end{array} \] Por tanto, \(e_2 = n\cdot 0.053=40\cdot 0.053=2.14.\)
Cálculo de \(p_3 = P(X_0\in \mbox{Clase }3)\): \[\scriptsize \begin{array}{rl} p_3 & = P(2.45 < X_0\leq 2.95)=P\left(\frac{2.45-3.5}{0.7} < Z \leq \frac{2.95-3.5}{0.7}\right) =P(-1.5 < Z\leq -0.786) \\ & =P(Z\leq -0.786)-P(Z\leq -1.5)=0.216-0.067=0.149. \end{array} \] Por tanto, \(e_3 = n\cdot 0.149=40\cdot 0.149=5.97.\)
Cálculo de \(p_4 = P(X_0\in \mbox{Clase }4)\): \[\scriptsize \begin{array}{rl}\scriptsize p_4 & = P(2.95 < X_0\leq 3.45)=P\left(\frac{2.95-3.5}{0.7} < Z \leq \frac{3.45-3.5}{0.7}\right) =P(-0.786 < Z\leq -0.071) \\ & =P(Z\leq -0.071)-P(Z\leq -0.786)=0.472-0.216=0.256. \end{array} \] Por tanto, \(e_4 = n\cdot 0.256=40\cdot 0.256=10.22.\)
Cálculo de \(p_5 = P(X_0\in \mbox{Clase }5)\): \[\scriptsize \begin{array}{rl} p_5 & = P(3.45 < X_0\leq 3.95)=P\left(\frac{3.45-3.5}{0.7} < Z \leq \frac{3.95-3.5}{0.7}\right) =P(-0.071 < Z\leq 0.643) \\ & =P(Z\leq 0.643)-P(Z\leq -0.071)=0.74-0.472=0.268. \end{array} \] Por tanto, \(e_5 = n\cdot 0.268=40\cdot 0.268=10.73.\)
Cálculo de \(p_6 = P(X_0\in \mbox{Clase }6)\): \[\scriptsize \begin{array}{rl} p_6 & = P(3.95 < X_0\leq 4.45)=P\left(\frac{3.95-3.5}{0.7} < Z \leq \frac{4.45-3.5}{0.7}\right) =P(0.643 < Z\leq 1.357) \\ & =P(Z\leq 1.357)-P(Z\leq 0.643)=0.913-0.74=0.173. \end{array} \] Por tanto, \(e_6 = n\cdot 0.173=40\cdot 0.173=6.91.\)
Cálculo de \(p_7 = P(X_0\in \mbox{Clase }7)\): \[\scriptsize p_7 = P(X_0\geq 4.45)=P\left(Z\geq \frac{4.45-3.5}{0.7}\right)=P(Z\geq 1.357)=0.087, \] donde \(Z=N(0,1)\). Por tanto, \(e_7 = n\cdot 0.087=40\cdot 0.087=3.49.\)
Observamos que las frecuencias teóricas \(e_1\), \(e_2\) y \(e_7\) son menores que 5. Por tanto, no se cumplen las condiciones para poder aplicar el contraste de bondad de ajuste.
Para solventar este problema, agruparemos los intervalos \((-\infty,1.95]\), \((1.95,2.45]\), \((2.45,2.95]\) en el intervalo \((-\infty, 2.95)\) y los intervalos \((3.95,4.45]\) y \((4.45,\infty)\) en el intervalo \((3.95,\infty)\). De esta forma, la tabla de frecuencias empíricas quedará de la forma siguiente:
| Rango de temperaturas | Frecuencias |
|---|---|
| \((-\infty,2.95]\) | \(2+1+4=7\) |
| \((2.95,3.45]\) | \(15\) |
| \((3.45,3.95]\) | \(10\) |
| \((3.95,\infty]\) | \(5+3=8\) |
Las frecuencias teóricas de la nueva tabla serán las siguientes:
- \(e_1 = 0.54+2.14+5.97 =8.64\).
- \(e_2 = n\cdot 0.256=40\cdot 0.256=10.22.\)
- \(e_3 = n\cdot 0.268=40\cdot 0.268=10.73.\)
- \(e_4 = 6.91+3.49= 10.41.\)
Ahora vemos que las frecuencias teóricas son mayores o iguales que 5 y, por tanto, se verifican las condiciones para poder aplicar el test de bondad de ajuste.
La tabla siguiente resume los cálculos realizados:
| Rango de temperaturas | Frecuencias empíricas | Frecuencias teóricas |
|---|---|---|
| \((-\infty,2.95]\) | \(7\) | \(8.64\) |
| \((2.95,3.45]\) | \(15\) | \(10.22\) |
| \((3.45,3.95]\) | \(10\) | \(10.73\) |
| \((3.95,\infty]\) | \(8\) | \(10.41\) |
El valor del estadístico de contraste \(\chi^2\) vale: \[ \chi_0 = \frac{(7-8.64)^2}{8.64}+ \frac{(15-10.22)^2}{10.22}+ \frac{(10-10.73)^2}{10.73}+\frac{(8-10.41)^2}{10.41}=3.153. \] El p-valor del contraste será: \[ p=P(\chi_{3} > 3.153)=0.369. \] Como el p-valor es grande, concluimos que no tenemos evidencias suficientes para rechazar que el aumento de temperatura no siga una distribución normal de parámetros \(\mu =3.5\) décimas de grado y \(\sigma =0.7\) décimas de grado.
Vamos a realizar el ejemplo anterior usando R.
En primer lugar, definimos las clases definiendo los extremos de los intervalos y las frecuencias empíricas:
extremos.izquierdos = c(-Inf,1.95,2.45,2.95,3.45,3.95,4.45)
extremos.derechos = c(1.95,2.45,2.95,3.45,3.95,4.45,Inf)
frecuencias.empíricas = c(2,1,4,15,10,5,3)
n=sum(frecuencias.empíricas)Para hallar las frecuencias teóricas usamos la función pnorm de R:
mu=3.5; sigma=0.7;
probabilidades.teóricas = pnorm(extremos.derechos,mu,sigma)-
pnorm(extremos.izquierdos,mu,sigma)
frecuencias.teóricas = n*probabilidades.teóricas
round(frecuencias.teóricas,2)## [1] 0.54 2.14 5.97 10.22 10.73 6.91 3.49Por último, aplicamos el test de la \(\chi^2\) usando la función chisq.test:
##
## Chi-squared test for given probabilities
##
## data: frecuencias.empíricas
## X-squared = 8.1, df = 6, p-value = 0.2R nos avisa que la aproximación \(\chi^2\) puede no ser correcta. Nosotros sabemos la razón: hay tres probabilidades teóricas que son menores que 5.
Llegados a este punto, podemos actuar de dos formas: juntamos intervalos o simulamos el p-valor.
Si optamos por la primera opción, tendremos que hacer:
extremos.izquierdos2=extremos.izquierdos[c(1,4,5,6)]
extremos.derechos2 = extremos.derechos[c(3,4,5,7)]
frecuencias.empíricas2 = c(sum(frecuencias.empíricas[1:3]),
frecuencias.empíricas[4:5],sum(frecuencias.empíricas[6:7]))
probabilidades.teóricas2 =pnorm(extremos.derechos2,mu,sigma)-
pnorm(extremos.izquierdos2,mu,sigma)
frecuencias.teóricas2 = n*probabilidades.teóricas2
chisq.test(frecuencias.empíricas2,p=probabilidades.teóricas2)##
## Chi-squared test for given probabilities
##
## data: frecuencias.empíricas2
## X-squared = 3.2, df = 3, p-value = 0.4Vemos que obtenemos los mismos valores que los cálculos realizados a mano.
Si optamos por la segunda opción, hemos de hacer:
##
## Chi-squared test for given probabilities with simulated p-value (based
## on 2000 replicates)
##
## data: frecuencias.empíricas
## X-squared = 8.1, df = NA, p-value = 0.2Aunque obtengamos un p-valor distinto, llegamos a la misma conclusión anterior.
5.1.6 Test \(\chi^2\) de Pearson con parámetros poblacionales desconocidos
El ejemplo visto anteriormente de normalidad no es realista en el sentido que la mayoría de las veces desconoceremos la media \(\mu\) y la desviación típica \(\sigma\) de la variable de la población \(X_0\) a la que se refiere la hipòtesis nula \(H_0\).
Cuando la variable \(X_0\) de la población de contraste dependa de algún(os) parámetro(s) desconocido(s), necesitamos conocer su valor de cara a calcular las frecuencias esperadas o frecuencias teóricas \(e_i\).
La manera de resolver este inconveniente, es estimar dichos parámetros usando el estimador máximo verosímil correspondiente.
Una vez estimados el(los) parámetro(s) del(de los) que depende la variable de la población \(X_0\), podemos realizar el test de bondad de ajuste tal como hemos visto pero ahora los grados de libertad de la distribución \(\chi^2\) disminuyen. En concreto, valen: \(k-1-\mbox{número de parámetros estimados.}\)
Ejemplo
Se quiere determinar si el número de veces que aparece la secuencia GATACA en una cadena de ADN de longitud 1000 sigue una ley Poisson.
Se toman varias muestras de cadenas de ADN de longitud 1000 y se cuentan los números de GATACA
| número \(x_i\) de veces queaparece GATACA | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| frecuencia empírica \(n_i\) | 229 | 211 | 93 | 35 | 7 | 1 |
Hemos realizado en total \(n=229 + 211+ 93+ 35 + 7 + 1=576\) observaciones.
El contraste a realizar es el siguiente: \[ \left\{ \begin {array}{ll} H_0: \mbox{La muestra proviene de una distribución } Po(\lambda),\\ H_1: \mbox{La muestra no proviene de esta distribución.} \end{array} \right.\]
Al no conocer el parámetro \(\lambda\), hemos de estimarlo.
Recordemos que el estimador máximo verosímil del parámetro \(\lambda\) de una distribución de Poisson es su media muestral: \(\hat{\lambda}=\overline{X}\): \[ \hat{\lambda} =\dfrac{229\cdot 0+ 211\cdot 1+ 93\cdot 2+ 35\cdot 3+7\cdot 4+ 1\cdot 5}{229+ 211+ 93 +35 + 7 + 1} =\dfrac{535}{576}=0.929. \]
Las clases deben cubrir todo el conjunto de valores de la variable \(X_0\) que, en nuestro caso, al ser una variable de Poisson, serían todos los enteros positivos: \(D_{X_0}=\{0,1,\ldots\}\).
Usando la tabla de frecuencias empíricas, consideramos las classes siguientes: \[ \begin{array}{rl} \mbox{Clase 0} & :{X_0=0},\ \mbox{Clase 1}:{X_0=1},\ \mbox{Clase 2}:{X_0=2},\ \mbox{Clase 3}:{X_0=3},\\ \mbox{Clase 4} & :{X_0=4},\ \mbox{Clase 5}:{X_0\geq 5}. \end{array} \]
Recordemos que la función de probabilidad de una variable de Poisson de parámetro \(\lambda\) vale: \(P(X_0=i)=\frac{\lambda^i}{i!}\mathrm{e}^{-\lambda}\), donde \(i\in D_{X_0}\).
Las frecuencias esperadas o teóricas \(e_i\) se calculan de la forma siguiente:
\(e_0 = n\cdot P(X_0\in \mbox{Clase }0)=n\cdot P(X_0 =0)=576\cdot \frac{0.929^0}{0!}\mathrm{e}^{-0.929}= 576\cdot \mathrm{e}^{-0.929}=227.53.\)
\(e_1 = n\cdot P(X_0\in \mbox{Clase }1)=n\cdot P(X_0 =1)=576\cdot \frac{0.929^1}{1!}\mathrm{e}^{-0.929}=211.34.\)
\(e_2 = n\cdot P(X_0\in \mbox{Clase }2)=n\cdot P(X_0 =2)=576\cdot \frac{0.929^2}{2!}\mathrm{e}^{-0.929}=98.15.\)
\(e_3 = n\cdot P(X_0\in \mbox{Clase }3)=n\cdot P(X_0 =3)=576\cdot \frac{0.929^3}{3!}\mathrm{e}^{-0.929}=30.39.\)
\(e_4 = n\cdot P(X_0\in \mbox{Clase }4)=n\cdot P(X_0 =4)=576\cdot \frac{0.929^4}{4!}\mathrm{e}^{-0.929}=7.06.\)
El cálculo de \(e_5\) se realiza de forma ligeramente diferente de los demás:
\[ \begin{array}{rl} e_5 & = n\cdot P(X_0\in \mbox{Clase }5)=n\cdot P(X_0 \geq 5)= n\cdot (1-P(X_0\leq 4)) \\ & =n\cdot (1-(P(X_0=0)+P(X_0=1)+P(X_0=2)+P(X_0=3)+P(X_0=4)))\\ & = 576-(227.53+ 211.34+98.15+30.39+7.06 )=1.54. \end{array} \] Como la clase 5 no verifica las condiciones de aplicación del contraste de bondad de ajuste al tener una frecuencia esperada menor que 5, juntaremos las dos últimas clases y las nuevas clases serán:
\[ \mbox{Clase 0}:{X_0=0},\ \mbox{Clase 1}:{X_0=1},\ \mbox{Clase 2}:{X_0=2},\ \mbox{Clase 3}:{X_0=3},\ \mbox{Clase 4}:{X_0\geq4}. \] Las frecuencias esperadas de las nuevas clases serán:
- \(e_0 = n\cdot P(X_0\in \mbox{Clase }0)=n\cdot P(X_0 =0)=227.53.\)
- \(e_1 = n\cdot P(X_0\in \mbox{Clase }1)=n\cdot P(X_0 =1)=211.34.\)
- \(e_2 = n\cdot P(X_0\in \mbox{Clase }2)=n\cdot P(X_0 =2)=98.15.\)
- \(e_3 = n\cdot P(X_0\in \mbox{Clase }3)=n\cdot P(X_0 =3)=30.39.\)
- El cálculo de \(e_4\) se realiza de forma parecida al cálculo de la clase 5 anterior: \[ \begin{array}{rl} e_4 & = n\cdot P(X_0\in \mbox{Clase }4)=n\cdot P(X_0 \geq 4)= n\cdot (1-P(X_0\leq 3)) \\ & =n\cdot (1-(P(X_0=0)+P(X_0=1)+P(X_0=2)+P(X_0=3))\\ & = 576-(227.53+ 211.34+98.15+30.39 )=8.6. \end{array} \]
Resúmamos en una tabla las frecuencias empíricas y las frecuencias esperadas:
| Clase | Frecuencias empíricas | Frecuencias teóricas |
|---|---|---|
| \(\{X_0=0\}\) | \(229\) | \(227.53\) |
| \(\{X_0=1\}\) | \(211\) | \(211.34\) |
| \(\{X_0=2\}\) | \(93\) | \(98.15\) |
| \(\{X_0 = 3\}\) | \(35\) | \(30.39\) |
| \(\{X_0\geq 4\}\) | \(7+1=8\) | \(8.6\) |
El valor del estadístico de contraste será: \[ \begin{array}{rl} \chi_0 & = \frac{(229-227.53)^2}{227.53}+\frac{(211-211.34)^2}{211.34}+\frac{(93-98.15)^2}{98.15}+\frac{(35-30.39)^2}{30.39}+\frac{(8-8.6)^2}{8.6} \\ & =1.022. \end{array} \]
Antes de calcular el p-valor del contraste, calculemos los grados de libertad de la variable \(\chi^2\). Éstos serán: \(g.l.=5-1-1=3\) ya que hemos estimado un parámetro, \(\lambda\).
El p-valor del contraste será: \[ p=P(\chi^2_3 > 1.022)=0.796. \] Como el p-valor es muy grande, concluimos que no tenemos evidencias suficientes para rechazar que el número de veces que aparece la secuencia GATACA en una cadena ADN de longitud 1000 sigue una ley de Poisson.
Resolvamos el ejemplo anterior con ayuda de R.
En primer lugar, definimos las frecuencias empíricas y las probabilidades esperadas y teóricas:
frecuencias.empíricas = c(229,211,93,35,8);
estimación.lambda = (211+93*2+35*3+7*4+1*5)/(229+211+93+35+7+1);
probabilidades.esperadas = c(dpois(0,estimación.lambda),dpois(1,estimación.lambda),
dpois(2,estimación.lambda),dpois(3,estimación.lambda),
1-ppois(3,estimación.lambda));A continuación, realizamos el test de bondad de ajuste usando la función chisq.test:
##
## Chi-squared test for given probabilities
##
## data: frecuencias.empíricas
## X-squared = 1, df = 4, p-value = 0.9Nos fijamos que el valor del estadístico de contraste coincide con el valor obtenido haciendo los cálculos a mano. Sin embargo, el p-valor no coincide. La razón es que R no tiene forma de saber si hemos estimado algún parámetro o no. Por este motivo, considera que los grados de libertad del estadístico de contraste son 4 en lugar de 3.
Entonces para hallar el p-valor correcto, hemos de usar la función pchisq:
test.chi2=chisq.test(frecuencias.empíricas,p=probabilidades.esperadas)
pchisq(test.chi2[[1]],3,lower.tail=FALSE)## X-squared
## 0.7959Comprobamos que ahora sí tenemos el p-valor correcto.
5.2 Contrastes donde la variable \(X_0\) es continua
En esta sección, vamos a ver contrastes específicos para comprobar si una variable sigue una determinada distribución continua.
El test de bondad de ajuste se puede aplicar en estos casos pero exige que el tamaño de la muestra \(n\) tiene que ser grande por dos razones: en primer lugar, \(n\) debe ser mayor que 30 y en segundo lugar, las frecuencias esperadas deben ser mayores que 5, condición que raramente se consigue para valores de \(n\) pequeños.
5.2.1 Test de Kolmogorov-Smirnov (K-S test)
El test de Kolgomorov-Smirnov (K-S) es un test genérico para contrastar la bondad de ajuste a distribuciones continuas.
Se puede usar con muestras pequeñas (se suele recomendar 5 elementos como el tamaño mínimo para que el resultado sea significativo), pero la muestra no puede contener valores repetidos: si los contiene, la distribución del estadístico de contraste bajo la hipótesis nula no es la que predice la teoría sino que solo se aproxima a ella, y por lo tanto los p-valores que se obtienen son aproximados.
El test K-S realiza un contraste en el que la hipótesis nula es que la muestra proviene de una distribución continua completamente especificada. Es decir, no sirve por ejemplo para contrastar si la muestra proviene de “alguna” distribución normal, sino solo para contrastar si proviene de una distribución normal con una media y una desviación típica concretas.
Por tanto, si queremos contrastar que la muestra proviene de alguna distribución de una familia concreta y estimamos sus parámetros a partir de la muestra, el test K-S solo nos permite rechazar o no la hipótesis de que la muestra proviene de la distribución de esa familia con exactamente esos parámetros.
Si el resultado es rechazar la hipótesis nula, significa que tenemos indicios suficientes para rechazar que la muestra proviene de la distribución de la familia con los parámetros que hemos especificado pero podría ser que la muestra siguiese una distribución de la misma familia con otros parámetros.
Sean \(x_1,x_2,\ldots,x_n\), con todos los valores diferentes tal como hemos comentado, y queremos contrastar si ha sido producida por una variable \(X\) con distribución \(F_X\).
Para aplicar el test K-S seguimos los pasos siguientes:
Ordenamos la muestra de menor a mayor: \(x_{(1)}< x_{(2)}<\cdots< x_{(n)}\).
Calculamos la función de distribución muestral \(F_{n}\) de esta muestra, definida de la forma siguiente: \[ F_n(x)=\left\{\begin{array}{ll} 0, &\mbox{ si } x< x_{(1)}, \\ \dfrac{k}{n}, &\mbox{ si } x_{(k)}\leq x < x_{(k+1)},\\[2ex] 1, & \mbox{ si } x_{(n)} \leq x. \end{array} \right. \] O sea, sería la función de distribución que corresponderia a la variable aleatoria discreta \(X_n\) con dominio \(D_X=\{x_{(1)}< x_{(2)}<\cdots< x_{(n)}\}\) y función de probabilidad \(P(X_n = x_{(i)})=\frac{1}{n}\), \(i=1,\ldots,n\).
El gráfico siguiente muestra la función de distribución muestral \(F_n\) para el caso en que la muestra sean los valores \(1,2,3,4,5\):
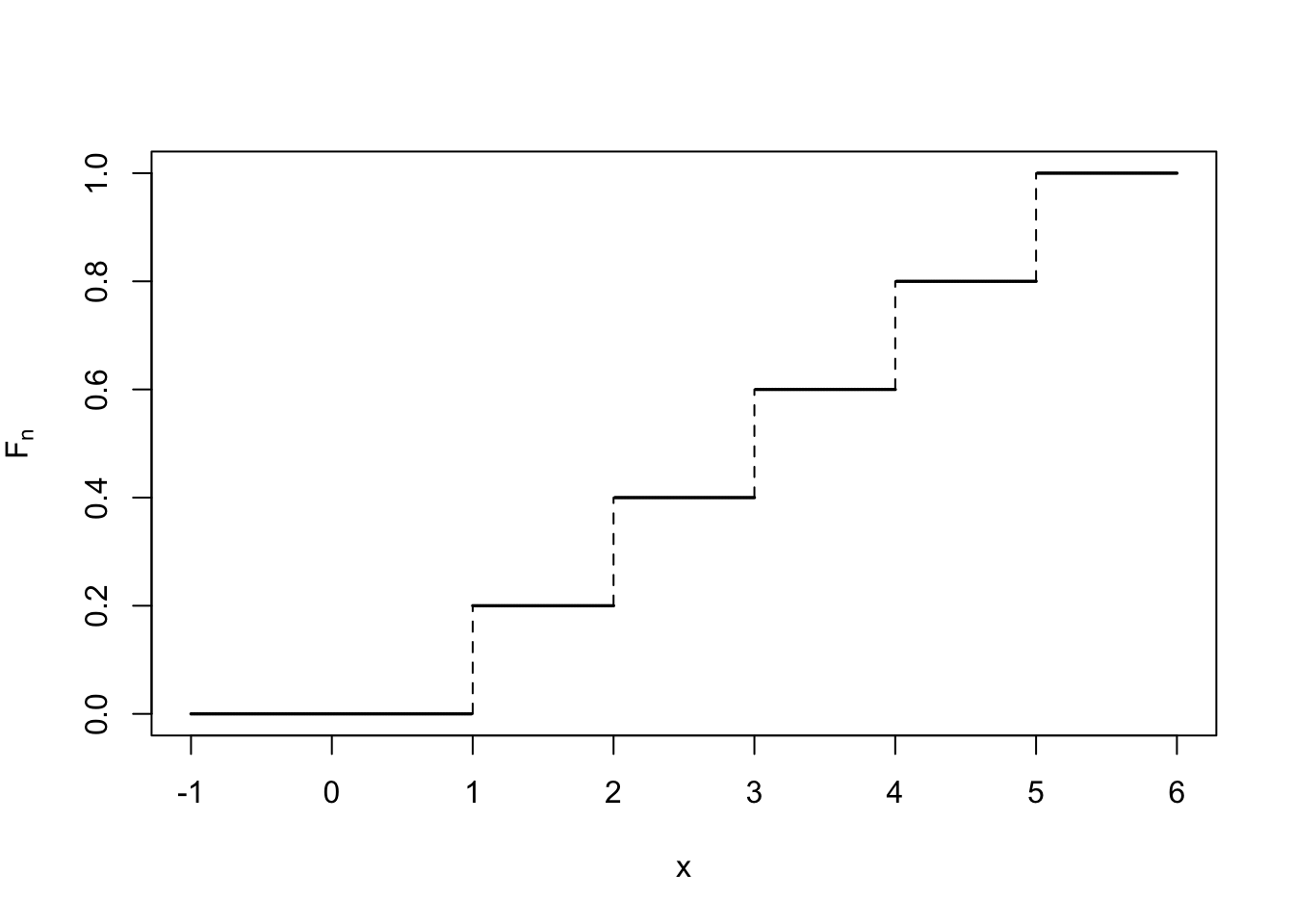
- El siguiente paso es comparar \(F_n(x)\) con \(F_X(x)\). Si son muy diferentes, concluimos que tenemos indicios suficientes para rechazar que la muestra proviene de la variable \(X\). ¿Cómo realizamos dicha comparación?
Calculamos \(\sup\{|F_n(x)-F_X(x)|\mid x\in \mathbb{R}\}\). Como \(F_X\) es creciente, este supremo se alcanza en algún extremo del “escalón” de la función \(F_n\).
Para calcular dicho supremo, calculamos la denominada discrepancia de cada valor \(x_{(i)}\): \[ \begin{array}{rl} D_n(x_{(i)})& \hspace{-1.5ex} =\max\big\{| F_X(x_{(i)})-F_{n}(x_{(i)}^{-})|, |F_{X}(x_{(i)})-F_n(x_{(i)})|\big\}\\[1ex] & \hspace{-1.5ex} \displaystyle=\max\Big\{\Big| F_X(x_{(i)})-\frac{i-1}{n}\Big|, \Big|F_{X}(x_{(i)})-\frac{i}{n}\Big|\Big\}, \end{array}\] para todos los \(i=1,\ldots, n\).
- El último paso es calcular la discrepancia máxima: \[ D_n=\max\big\{D_n(x_{(i)})\mid i=1,\ldots, n\big\}. \]
El resultado interesante viene ahora:
En la práctica, se aproxima \(D_n \approx \frac{1}{\sqrt{n}}\cdot K\) y se calcular el p-valor como:
\[
p=P\left(D_n > d_n\right),
\]
donde \(d_n\) representa el valor obtenido de la variable \(D_n\) usando nuestra muestra. La probabilidad anterior se calcula usando la función de distribución de la variable \(\frac{1}{\sqrt{n}}\cdot K\). Dicha función de distribución está tabulada o hay que usar R.
Ejemplo
Queremos decidir si los valores \[ 5.84,4.57,1.34,3.58,1.54,2.25 \] provienen de una distribución normal con \(\mu=3\) y \(\sigma=1.5\).
El contraste a realizar es el siguiente:
\[
\left\{
\begin{array}{l}
H_0: \mbox{ la muestra proviene de una $X\sim N(3,1.5)$,}\\
H_0: \mbox{ la muestra no proviene de una $X\sim N(3,1.5).$}
\end{array}
\right.
\]
Para aplicar el test K-S, primero ordenamos la muestra usando R “como calculadora”:
## [1] 1.34 1.54 2.25 3.58 4.57 5.84A continuación, calculamos la función de distribución muestral \(F_{n}\): \[ F_n(x)=\left\{\begin{array}{ll} 0, &\mbox{ si } x< 1.34, \\ \frac{1}{6}, & \mbox{ si } 1.34\leq x < 1.54,\\[1ex] \frac{2}{6}, & \mbox{ si } 1.54\leq x < 2.25,\\[1ex] \frac{3}{6}, & \mbox{ si } 2.25\leq x < 3.58,\\[1ex] \frac{4}{6}, & \mbox{ si } 3.58\leq x < 4.57,\\[1ex] \frac{5}{6}, & \mbox{ si } 4.57\leq x < 5.84,\\[1ex] 1, & \mbox{ si } 5.84 \leq x, \end{array} \right. \]
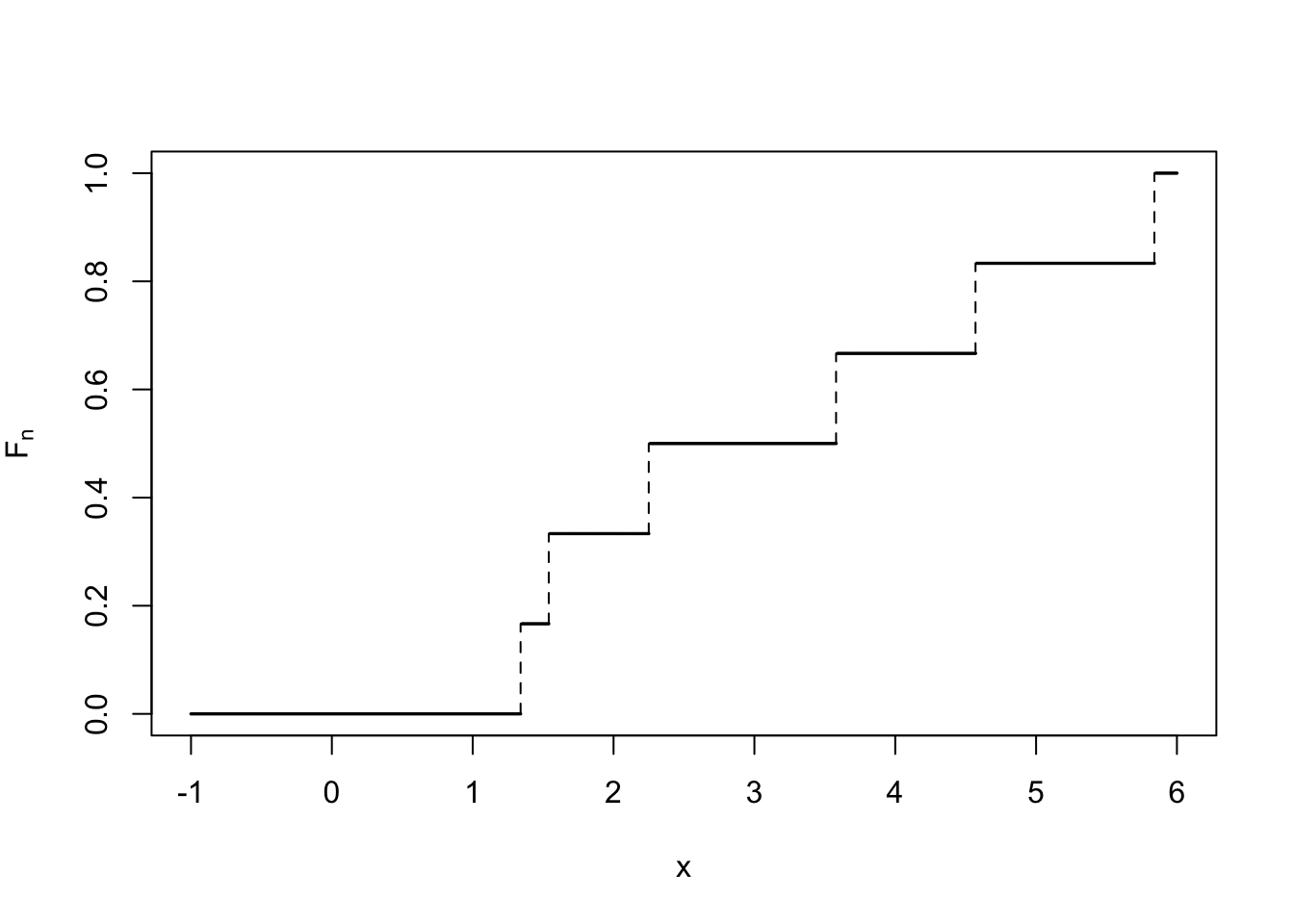
Calculamos la discrepancia de cada observación \(x_{(i)}\) que recordemos que vale: \[ D_n(x_{(i)})=\max\Big\{\Big| F_X(x_{(i)})-\frac{i-1}{n}\Big|, \Big|F_{X}(x_{(i)})-\frac{i}{n}\Big|\Big\}. \] Esquematizemos los resultados en la tabla siguiente donde \(Z\) representa la normal estándar \(N(0,1)\):
| \(i\) | \(x_{(i)}\) | \(F_X(x_{(i)})\) | \(\Big| F_X(x_{(i)})-\frac{i-1}{6}\Big|\) | \(\Big|F_{X}(x_{(i)})-\frac{i}{6}\Big|\) | \(D_6(x_{(i)})\) |
|---|---|---|---|---|---|
| \(1\) | \(1.34\) | \(F_X(1.34)=F_Z\left(\frac{1.34-3}{1.5}\right)=0.134\) | \(0.134\) | \(\left|\frac{1}{6}-0.134\right|\)=\(0.032\) | \(0.134\) |
| \(2\) | \(1.54\) | \(F_X(1.54)=F_Z\left(\frac{1.54-3}{1.5}\right)=0.165\) | \(\left|0.165-\frac{1}{6}\right|=0.001\) | \(\left|0.165-\frac{2}{6}\right|=0.168\) | \(0.168\) |
| \(3\) | \(2.25\) | \(F_X(2.25)=F_Z\left(\frac{2.25-3}{1.5}\right)=0.309\) | \(\left|0.309-\frac{2}{6}\right|=0.025\) | \(\left|0.309-\frac{3}{6}\right|=0.191\) | \(0.191\) |
| \(4\) | \(3.58\) | \(F_X(3.58)=F_Z\left(\frac{3.58-3}{1.5}\right)=0.65\) | \(\left|0.65-\frac{3}{6}\right|=0.15\) | \(\left|0.65-\frac{4}{6}\right|=0.016\) | \(0.15\) |
| \(5\) | \(4.57\) | \(F_X(4.57)=F_Z\left(\frac{4.57-3}{1.5}\right)=0.852\) | \(\left|0.852-\frac{4}{6}\right|=0.186\) | \(\left|0.852-\frac{5}{6}\right|=0.019\) | \(0.186\) |
| \(6\) | \(5.84\) | \(F_X(5.84)=F_Z\left(\frac{5.84-3}{1.5}\right)=0.971\) | \(\left|0.971-\frac{5}{6}\right|=0.138\) | \(\left|0.971-1\right|=0.029\) | \(0.138\) |
El valor del estadístico \(D_6\) será el máximo de la última columna de la tabla anterior: \(D_6 =0.191.\)
De cara a hallar el p-valor tenemos que consultar la tabla del test de Kolmogorov-Smirnov. Si vais a http://images.google.com y escribís “tabla de dn Kolmogorov” en la casilla de búsqueda, encontraréis un montón de tablas de la variable \(D_n\).
La primera fila de dichas tablas corresponde al error tipo I del contraste y la primera columna, al tamaño de la muestra \(n\).
Si os fijáis en la fila correspondiente a \(n=6\), veréis que el valor de \(D_6=0.191\) no sale, lo que significa que el valor \(\alpha\) debe ser mayor que 0.2. Por tanto, nuestro p-valor serà mayor que 0.2, hecho que nos hace concluir que no tenemos indicios suficientes para rechazar que la muestra se distribuya según una distribución normal \(N(\mu=3,\sigma=1.5)\).
5.2.2 Contraste K-S en R
La función básica para realizar el test K-S es ks.test. Su sintaxis
básica para una muestra es
donde:
xes la muestra de una variable continua.ypuede ser un segundo vector, y entonces se contrasta si ambos vectores han sido generados por la misma distribución continua, o el nombre de la función de distribución (empezando conp) que queremos contrastar, entre comillas; por ejemplo"pnorm"para la distribución normal.Los
parámetrosde la función de distribución si se ha especificado una; por ejemplomean=0, sd=1para una distribución normal estándar.
Ejemplo anterior con R
Para realizar el contraste K-S para nuestro ejemplo, tenemos que hacer lo siguiente:
##
## One-sample Kolmogorov-Smirnov test
##
## data: muestra
## D = 0.19, p-value = 0.9
## alternative hypothesis: two-sidedObservamos que nos da el mismo valor de discrepancia máxima que hemos obtenido anteriormente con un p-valor altísimo, hecho que corrobora la conlusión que hemos escrito.
5.3 Tests de normalidad
5.3.1 Test de Kolmogorov-Smirnov-Lilliefors (K-S-L)
Para contrastar si una muestra proviene de una distribución normal con los parámetros \(\mu\) y \(\sigma\) desconocidos, el test K-S nos “obliga” a darles un valor.
Los valores “óptimos” para dichos parámetros serían las estimaciones dadas por los estimadores de máxima verosimilitud: la media muestral para \(\mu\) y la desviación típica muestral para sigma.
La prueba de Kolmogorov-Smirnov-Lilliefors consiste en estimar dichos parámetros, calcular la discrepancia máxima tal como hemos explicado pero a la hora de calcular el p-valor, se usa otra distribución, llamada distribución de Lilliefors en lugar de usar la distribución de Kolmogorov ya que con la distribución de Lilliefors, el contraste es más robusto.
Vamos a aplicar el test K-S-L a nuestra muestra anterior para ver si se distribuye según la ley normal.
El test K-S-L test en R se aplica usando la función lillie.test del paquete nortest:
##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: muestra
## D = 0.2, p-value = 0.6Vemos que el p-valor no es tan grande como en el caso anterior pero aún así, es suficientemente grande para concluir que no tenemos indicios suficientes para rechazar que nuestra muestra siga la distribución normal.
El test K-S-L tiene un inconveniente: aunque es muy sensible a las diferencias entre la muestra y la distribución teórica alrededor de sus valores medios, le cuesta detectar diferencias prominentes en un extremo u otro de la distribución.
Su potencia se ve afectada por dicho inconveniente.
Veamos un ejemplo de este hecho intentando ver si una muestra de una distribución \(t\) de Student nos acepta que es normal o no:
##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: x
## D = 0.1, p-value = 0.2Nos dice que no podemos rechazar que la muestra x sea normal.
Esto es debido a que la función de densidad de la distribución \(t\) de Student es algo más aplanada que la distribución normal, donde en los dos extremos está por encima de la de la normal.
Como el test K-S-L no detecta las diferencias en los extremos, acepta que x es normal.
5.3.2 Test de normalidad de Anderson-Darling (A-D)
El test de normalidad de Anderson-Darling resuelve el inconveniente del test de K-S-L.
Este test está implementado en la función ad.test del paquete nortest.
Si ahora, aplicamos el test A-D a la muestra anterior de la distribución \(t\) de Student, la normalidad queda rechazada:
##
## Anderson-Darling normality test
##
## data: x
## A = 1.2, p-value = 0.004Un inconveniente común a los tests K-S-L y A-D es que, si bien pueden usarse con muestras pequeñas (pongamos de más de 5 elementos), se comportan mal con muestras grandes, de varios miles de elementos.
En muestras de este tamaño, cualquier pequeña divergencia de la normalidad se magnifica y en estos dos tests aumenta la probabilidad de errores de tipo I.
5.3.3 Test de Shapiro-Wilks (S-W)
Un test que resuelve este problema es el de Shapiro-Wilk (S-W), implementado en la función shapiro.test de la instalación básica de R.
Apliquemos el test S-W a las dos muestras anteriores: la muestra del ejemplo y la muestra de la distribución \(t\) de Student:
##
## Shapiro-Wilk normality test
##
## data: muestra
## W = 0.93, p-value = 0.5##
## Shapiro-Wilk normality test
##
## data: x
## W = 0.89, p-value = 0.0003Vemos que acepta que la muestra del ejemplo anterior sea normal y rechaza la normalidad en el caso de la muestra de la \(t\) de Student.
Si nuestra muestra de valores tiene empates, los p-valores de los contrastes calculados a partir de las distribuciones de los estadísticos usados en los tests K-S-L, A-D y S-W se pueden ver afectados hasta el punto de que, si hay muchos empates, su significado no tenga ningún sentido.
Hay que decir que el menos afectado por los empates es el test de S-W.
5.3.4 Test omnibus de D’Agostino-Pearson
Un test que no es sensible a los empates es el test de normalidad de D’Agostino-Pearson.
Este test se encuentra implementado en la función dagoTest del paquete fBasics, y lo que hace es cuantificar lo diferentes que son la asimetría y la curtosis de la muestra (dos parámetros estadísticos relacionados con la forma de la gráfica de la función de densidad muestral) respecto de los esperados en una distribución normal, y resume esta discrepancia en un p-valor con el significado usual.
Para poder aplicar dicho test, el tamaño de la muestra debe ser 20 como mínimo.
Por tanto, sólo podemos aplicar dicho test a la muestra de datos correspondiente a la distribución \(t\) de Student:
##
## Title:
## D'Agostino Normality Test
##
## Test Results:
## STATISTIC:
## Chi2 | Omnibus: 21.8125
## Z3 | Skewness: 2.8069
## Z4 | Kurtosis: 3.7328
## P VALUE:
## Omnibus Test: 0.00001834
## Skewness Test: 0.005001
## Kurtosis Test: 0.0001894
##
## Description:
## Thu Oct 14 12:41:56 2021 by user:Si nos fijamos en el resultado, el test calcula tres estadísticos de contraste: el test Omnibus basado en la distribución \(\chi^2\), el test de asimetría y el test de curtosis con sus correspondientes p-valores. Para más información, id a https://en.wikipedia.org/wiki/D%27Agostino%27s_K-squared_test
Vemos que según el test de D’Agostino-Pearson, la muestra x correspondiente a la distribución \(t\) de Student no sigue la ley normal.
5.4 Guía rápida
qqPlotdel paquete car, sirve para dibujar un Q-Q-plot de una muestra contra una distribución teórica. Sus parámetros principales son:distribution: el nombre de la familia de distribuciones, entre comillas.- Los parámetros de la distribución:
meanpara la media,sdpara la desviación típica,dfpara los grados de libertad, etc. - Los parámetros usuales de
plot.
chisq.testsirve para realizar tests \(\chi^2\) de bondad de ajuste. Sus parámetros principales son:p: el vector de probabilidades teóricas.rescale.p: igualado aTRUE, indica que los valores depno son probabilidades, sino sólo proporcionales a las probabilidades.simulate.p.value: igualado aTRUE, R calcula el p-valor mediante simulaciones.B: en este último caso, permite especificar el número de simulaciones.
ks.testrealiza el test de Kolmogorov-Smirnov. Tiene dos tipos de uso:ks.test(x,y): contrasta si los vectoresxeyhan sido generados por la misma distribución continua.ks.test(x, "distribución", parámetros): contrasta si el vectorxha sido generado por la distribución especificada, que se ha de indicar con el nombre de la función de distribución de R (la que empieza con p).
lillie.testdel paquete nortest, realiza el test de normalidad de Kolmogorov-Smirnov-Lilliefors.ad.testdel paquete nortest, realiza el test de normalidad de Anderson-Darling.shapiro.test, realiza el test de normalidad de Shapiro-Wilk.dagoTestdel paquete fBasics, realiza el test ómnibus de D’Agostino-Pearson.