Preliminares

0.1 Cuerpos

0.1.1 La estructura de cuerpo

Cuerpo. Sea $\mathbb{K}$ un conjunto dotado de dos operaciones, adición ($+$) y multiplicación ($\cdot$). Diremos que $\mathbb{K}$ es un cuerpo si para todo $a,b\in\mathbb{K}$ se cumplen las condiciones siguientes:

$+$ y $\cdot$ son operaciones internas sobre $\mathbb{K}$: $a+b\in\mathbb{K}$ y $a\cdot b\in\mathbb{K}$
$+$ y $\cdot$ son operaciones conmutativas: $a+b=b+a$ y $a\cdot b=b\cdot a$
$+$ y $\cdot$ son operaciones asociativas: $(a+b)+c=a+(b+c)$ y $(a\cdot b)\cdot c=a\cdot(b\cdot c)$
Hay un elemento neutro para la adición: $a+0=0+a=a\quad \forall a\in\mathbb{K}$
Hay un elemento neutro para la multiplicación (distinto del neutro de la adición): $a\cdot 1=1\cdot a=a\quad \forall a\in\mathbb{K}$
Elemento opuesto: $\forall a\in\mathbb{K}$ hay otro elemento $-a\in\mathbb{K}$ tal que $a+(-a)=(-a)+a=0$
Elemento inverso: $\forall a\in\mathbb{K},\ a\ne 0$ hay otro elemento $a^{-1}\in\mathbb{K}$ tal que $a\cdot a^{-1}=a^{-1}\cdot a=1$
La operación $\cdot$ es distributiva respecto $+$: $a\cdot(b+c)=a\cdot b+a\cdot c$

Observación. Cuando no pueda haber confusión quitaremos el signo $\cdot$ para denotar la operación de multiplicación. Es decir, denotaremos $a\cdot b$ como $ab$.

0.1.2 Propiedades de los cuerpos

Propiedades de los cuerpos. En un cuerpo $\mathbb{K}$ se verifican las siguientes propiedades:

Propiedad de simplificación para la suma: $a+b=a+c\Rightarrow\ b=c$
Los neutros (0 y 1) son únicos
Cada elemento tienen un único opuesto
Cada elemento diferente de 0 tiene un único inverso
0 es absorbente para la multiplicación: $a\cdot 0 = 0\quad \forall a\in\mathbb{K}$
$\mathbb{K}$ no tiene divisores de 0: $ab=0\Rightarrow a=0$ o $b=0$

¡Atención! La demostración de esta proposición se encuentra en pdf. Este pdf lo podréis encontrar en el Github, en la carpeta demostraciones, o bien como material de esta clase.

0.1.3 Cuerpos conocidos

Ejemplo 1

Algunos de los cuerpos más conocidos son:

$\mathbb{Z}_2=\{0,1\}$: Cuerpo finito de dos elementos
$\mathbb{Q}$: Los números racionales
- suma: $\frac{a}{b}+\frac{c}{d} = \frac{ad+bc}{bd}$ $\qquad a,b,c,d\in\mathbb{Z}$
- producto: $\frac{a}{b}\cdot\frac{c}{d} = \frac{ac}{bd}$ $\qquad a,b,c,d\in\mathbb{Z}$
$\mathbb{R}$: Los números reales
$\mathbb{C}$: Los números complejos
- suma: $(a+bi)+(c+di) = (a+c)+(b+d)i$ $\qquad a,b,c,d\in\mathbb{R}$
- producto: $(a+bi)\cdot(c+di) = (ac-bd)+(ad+bc)i$ $\qquad a,b,c,d\in\mathbb{R}$

Ejemplo 2

Los números naturales, $\mathbb{N}:=\{0,1,2,...\}$, no son un cuerpo. No hay elementos opuestos para ningún elemento del conjunto.

0.1.4 El cuerpo $\mathbb{Z}_2$

Entremos un poquito más en detalle en este cuerpo tan interesante:

Consta de 2 elementos: el 0 y el 1
Sus tablas de suma y producto son las siguientes

Tabla de la suma

Tabla del producto

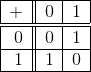
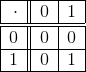
0.2 Números complejos

Conjunto de Números Complejos. $\mathbb{C}=\{(a,b):a,b\in\mathbb{R}\}$ dotado de las operaciones:

suma: $(a,b)+(c,d) = (a+c,b+d)$ $\qquad a,b,c,d\in\mathbb{R}$
producto: $(a,b)\cdot(c,d) = (ac-bd,ad+bc)$ $\qquad a,b,c,d\in\mathbb{R}$

Forma Binómica. Si $z\in\mathbb{C}$ tal que $z=(a,b)$, su forma binómica es $z=a+bi$

La forma binómica aparece al definir la unidad imaginaria, $i$:

Unidad Imaginaria. $i=(0,1)$

Entonces, si $z=(a,b)$, tenemos que

\[z=(a,b)=(a,0)+(0,b)=(a,0)+(b,0)\cdot(0,1)=a+bi\]

Parte Real. Si $z=a+bi$, Re$(z)=a$

Parte Imaginaria. Si $z=a+bi$, Im$(z)=b$

Conjugado de z. Si $z=a+bi$, $\bar{z}=a-bi$

Módulo. $|z|=\sqrt{z\cdot\bar{z}}$

Argumento. Si $z=a+bi$, $\text{arg}(z)=\arctan\left(\frac{b}{a}\right)$. Se da en radianes.

Argumento principal. $\text{Arg}(z)\in(-\pi,\pi]$

0.2.1 Plano Complejo

Los números complejos se suelen representar en un plano, denominado plano complejo, donde el eje de las abcisas es el eje Real y, el de las ordenadas, el eje Imaginario

0.2.2 Forma polar

Fórmula de Euler. $e^{i\theta}=\cos(\theta)+i\sin(\theta)$

Forma polar. $z=re^{i\varphi}$ donde $r = |z|$ y $\varphi = \text{arg}(z)$

0.2.3 Números complejos con `R`

Podemos definir números complejos de diferentes formas:

z1 = 2+1i #Definimos el complejo en forma binómica
z1

[1] 2+1i

z2 = complex(real = 2, imaginary = -1) #Definimos mediante parte real e imaginaria
z2

[1] 2-1i

z3 = complex(modulus = 2, argument = pi) #Definimos mediante módulo y argumento
z3

[1] -2+0i

¡Observación! Si queremos escribir los números complejos $a+i$ o $a-i$ en R, donde $a$ puede ser cualquier número real, lo tenemos que hacer del siguiente modo: a+1i o a-1i, ya que si no la consola nos devolverá error.

La función typeof() es útil a la hora de comprobar el tipo de dato con el que estamos trabajando:

typeof(z1)

[1] "complex"

typeof(z2)

[1] "complex"

typeof(z3)

[1] "complex"

Para obtener la parte real y la parte imaginaria de cualquier número complejo, utilizamos, respectivamente, las funciones Re() e Im():

#Parte Real
Re(z1)

[1] 2

#Parte Imaginaria
Im(z3)

[1] 2.449294e-16

El conjugado de un número complejo se obtiene mediante la función Conj():

Conj(z1)

[1] 2-1i

Conj(z2)

[1] 2+1i

Conj(z3)

[1] -2-0i

Para obtener el módulo y el argumento (principal) de cualquier número complejo, utilizamos, respectivamente, las funciones Mod() y Arg():

#Módulo
Mod(z2)

[1] 2.236068

#Argumento principal
Arg(z3)

[1] 3.141593

Las operaciones básicas con números complejos se realizan del siguiente modo:

z1+z2 #Suma de números complejos

[1] 4+0i

3*z3 #Producto por un escalar

[1] -6+0i

z2*z3 #Producto de números complejos

[1] -4+2i

0.2.4 Trabajando con `Python` en Markdown

En primer lugar, tendréis que instalar el paquete de R llamado reticulate del siguiente modo:

install.packages(''reticulate'')

Si en algún momento necesitáis instalar una librería de Python en Rstudio, se debe ejecutar la siguiente función:

py_install("NombreDelPaquete")

Para poder utilizar Python en un Markdown, en el chunk de ajustes deberéis añadir las instrucciones que se muestran a continuación

library(reticulate)
use_python("/anaconda3/bin/python3")

La primera para cargar la librería reticulate y la segunda para ubicar donde está Python en nuestro ordenador

0.2.5 Números complejos con `Python`

Podemos definir números complejos de diferentes formas:

z1 = 4+3j
z1

(4+3j)

z2 = complex(1,7)
z2

(1+7j)

¡Observación! Si queremos escribir los números complejos $a+i$ o $a-i$ en Python, donde $a$ puede ser cualquier número real, lo tenemos que hacer del siguiente modo: a+ji o a-ji, ya que si no la consola nos devolverá error.

La función type() es útil a la hora de comprobar el tipo de dato con el que estamos trabajando:

type(z1)

<class 'complex'>

type(z2)

<class 'complex'>

Para obtener la parte real y la parte imaginaria de cualquier número complejo, utilizamos, .real y .imag

z1.real #Parte real

4.0

z2.imag #Parte imaginaria

7.0

El conjugado de un número complejo se obtiene mediante .conjugate():

z1.conjugate()

(4-3j)

z2.conjugate()

(1-7j)

Para obtener el módulo y el argumento (principal) de cualquier número complejo, utilizamos, respectivamente, las funciones abs() y cmath.phase():

import cmath
abs(z1)

5.0

cmath.phase(z2)

1.4288992721907328

Las operaciones básicas con números complejos se realizan del siguiente modo:

z1+z2 #Suma de numeros complejos

(5+10j)

5*z2 #Producto por un escalar

(5+35j)

z1*z2 #Producto de numeros complejos

(-17+31j)

0.2.6 Trabajando con `Octave` en Markdown

Para poder utilizar Octave en Markdown deberéis introducir en el chunk de ajustes el siguiente código:

knitr::opts_chunk$set(echo = TRUE, engine.path = list( octave = '/Applications/Octave-4.4.1.app/Contents/Resources/usr/bin/octave'))

Lo que está entre comillas es la dirección donde se encuentra el lenguaje Octave en nuestro ordenador

¡Ojo! A la hora de utilizar chunks de Octave, tendréis que introducir las variables cada vez. Es decir, no se guarda la información de un chunk a otro

0.2.7 Números complejos con `Octave`

Podemos definir números complejos de diferentes formas:

z1 = complex(1,2)
z2 = 2-i
tipoDato1 = class(z1)
tipoDato2 = class(z2)

z1 =  1 + 2i
z2 =  2 - 1i
tipoDato1 = double
tipoDato2 = double

La función class() es útil a la hora de comprobar el tipo de dato con el que estamos trabajando.

Para obtener la parte real y la parte imaginaria de cualquier número complejo, utilizamos, respectivamente, las funciones real() e imag()

z1 = complex(1,2);
z2 = 2-i;

real(z1)
imag(z2)

ans =  1
ans = -1

Observación. Para trabajar con los números complejos anteriormente definidos, hemos tenido que crearlos de nuevo porque Octave trata cada chunk por separado.

El conjugado de un número complejo se obtiene mediante la función conj():

z1 = complex(1,2);
z2 = 2-i;

conj(z1)
abs(z2)
arg(z1)
angle(z2)

ans =  1 - 2i
ans =  2.2361
ans =  1.1071
ans = -0.46365

Para obtener el módulo y el argumento (principal) de cualquier número complejo, utilizamos, respectivamente, las funciones abs() y arg() o angle().

Las operaciones básicas con números complejos se realizan del siguiente modo:

z1 = complex(1,2);
z2 = 2-i;

#Suma de numeros complejos
z1+z2
## Producto por un escalar
8*z2
## Producto de numeros complejos
z1*z2

ans =  3 + 1i
ans =  16 -  8i
ans =  4 + 3i

0.3 Polinomios

Sea $\mathbb{K}$ un cuerpo cualquiera

Polinomio en una variable. Objeto de la forma $p(x)=a_0+a_1x+\cdots+a_nx^n$ donde $a_i\in\mathbb{K}\quad \forall i=0,\dots,n$

Polinomio iguales. Dos polinomios son iguales si tienen el mismo grado y los mismos coeficientes. Es decir, dados $p(x) = a_0+a_1x+\cdots+a_nx^n$ y $q(x) = b_0+b_1x+\cdots+b_mx^m$, $p$ y $q$ son iguales si, y solo si, $n = m$ y $a_i=b_i\quad \forall i=0,1,\dots,n$

Grado de un polinomio. Si $a_n\ne 0$ y $a_j = 0\ \forall j=n+1,n+2,\dots$, se dice que el grado del polinomio es $n$.

Ejemplo 3

$p(x)=x^2+5x+1$ es un polinomio de segundo grado (grado 2)
$q(x)=x^4-5$ es un polinomio de grado 4

Polinomio 0. $p(x)=0$. Es decir, $a_i=0$ para todo $i=0,\dots,n$

Polinomio constante. Polinomio de grado 0

Ejemplo 4

$p(x)=5$ es un polinomio constante

Conjunto de polinomios en una variable. Indicaremos por $\mathbb{K}[x]$ el conjunto de polinomios en una determinada variable $x$ y con coeficientes en $\mathbb{K}$. Sobre $\mathbb{K}[x]$ se pueden considerar la adición y la multiplicación definidas a partir de las operaciones de $\mathbb{K}$ de la manera siguiente

$p(x)+q(x)$ es el polinomio que tiene por coeficientes la suma (en $\mathbb{K}$) de los coeficientes de $p(x)$ y $q(x)$. Más claramente, si $p(x)=a_0+a_1x+\cdots+a_nx^n$ y $q(x)=b_0+b_1x+\cdots+b_mx^m$, entonces $p(x)+q(x)=(a_0+b_0)+(a_1+b_1)x+\cdots$
$p(x)q(x)$ es el polinomio $c_0+c_1(x)+\cdots+c_{nm}x^{n+m}$ donde $c_j=a_0b_j+a_1b_{j-1}+\cdots+a_jb_0$ $\quad j=0,1,\dots,n+m$

Ejemplo 5

Sean $p(x) = x+1$ y $q(x) = x-1$. Entonces,

Su suma es $p(x)+q(x)=(x+1)+(x-1) = (1+1)x+(1-1) = 2x+0=2x$
Su producto es $p(x)\cdot q(x)=(x+1)\cdot(x-1)=x^2+x-x-1=x^2-1$

Con estas operaciones el conjunto $\mathbb{K}[x]$ presenta una serie de propiedades importantes que no permiten decir que es un cuerpo. La condición de cuerpo que nos falla aquí es únicamente que no existe elemento inverso para todo elemento de $\mathbb{K}[x]$. De hecho, los únicos elementos que tienen inverso son los polinomios constantes y diferentes de 0.

División de polinomios. Dado un polinomio $p(x)\in\mathbb{K}[x]$, la división de $p(x)$ entre otro polinomio $s(x)\in\mathbb{K}[x]$ de grado menor o igual al de $p(x)$, consiste en hallar 2 polinomios $q(x),r(x)\in\mathbb{K}[x]$ tales que \[p(x) = s(x)q(x)+r(x)\]

donde el grado de $r(x)$ es siempre menor que el del divisor $s(x)$

Polinomio irreducible. Si es un polinomio con coeficientes en un cuerpo, no es constante y no se puede descomponer en producto de otros polinomios sin que esta descomposición sea trivial.

Ejemplo 6

$p(x) = 1+x^2\in\mathbb{R}[x]$ es irreducible ya que no puede escribirse de forma $r(x)s(x)$ con $r(x),s(x)\in\mathbb{R}[x]$, $r(x),s(x)\ne p(x)$ y $r(x),s(x)\ne 1$.

En cambio, $q(x)=1-x^2$ no es irreducible, ya que $q(x)=(1-x)(1+x)$

Dado un polinomio $p(x)\in\mathbb{K}[x]$, podemos asociar a $p(x)$ una aplicación o función $\mathbb{K}\longrightarrow\mathbb{K}$ definida de la manera siguiente: a cada elemento $\alpha\in\mathbb{K}$ le hacemos corresponder $p(\alpha)=a_0+a_1\alpha+\cdots+a_n\alpha^n$. Esta función es conocida como función evaluadora y el proceso de sustituir la variable $x$ por cualquier elemento $\alpha$ del cuerpo se lo conoce como evaluar un polinomio en $\alpha$.

En el caso en que $\mathbb{K}$ sea un cuerpo infinito, podemos identificar polinomio con función asociada.

Raíz de un polinomio. Sean $p(x)\in\mathbb{K}[x]$ y $\alpha\in\mathbb{K}$, diremos que $\alpha$ es raíz de $p(x)$ si $p(\alpha)=0$.

Proposición. $\alpha\in\mathbb{K}$ es raíz de $p(x)$ $\Leftrightarrow$ $p(x)=(x-\alpha)q(x)$ con $q(x)\in\mathbb{K}[x]$.

De aquí deducimos que si un polinomio de $\mathbb{K}[x]$ de grado mayor que 1 tiene una raíz (en $\mathbb{K}$) entonces no es irreducible. El recíproco no es cierto.

Demostración

Primero probaremos la implicación hacia la izquierda, $p(x)=(x-\alpha)q(x)$ con $q(x)\in\mathbb{K}[x]\Rightarrow$$\alpha\in\mathbb{K}$ es raíz de $p(x)$

Evaluando $p(x)$ en $\alpha$ tenemos que \[p(\alpha)=(\alpha-\alpha)q(\alpha) = 0\] lo que, por definición, implica que $\alpha$ es raíz de $p(x)$

Ahora nos queda demostrar la implicación a la derecha $\alpha\in\mathbb{K}$ es raíz de $p(x)$ $\Rightarrow$ $p(x)=(x-\alpha)q(x)$ con $q(x)\in\mathbb{K}[x]$

Si dividimos $p(x)$ entre $x-\alpha$, obtenemos \[p(x) = (x-\alpha)q(x)+r(x)\]

Ahora, por hipótesis tenemos que \[p(\alpha) = (\alpha-\alpha)q(\alpha)+r(\alpha) = 0 +r(\alpha) = 0\]

Con lo cual $r(\alpha) = 0$

Ahora bien, el grado de $r(x)$ debe ser estrictamente menor al del divisor, $x-\alpha$, que es 1. Por tanto, $r(x)$ es un polinomio constante. Además, como $r(\alpha) =0$, tenemos que \[r(x)\equiv 0\]

Así pues, acabamos de demostrar que $p(x) = (x-\alpha)q(x)$

0.3.1 Polinomios con `R`

Necesitaremos instalar y cargar los paquetes polynom y pracma para poder utilizar las siguientes funciones.

Para definir un polinomio en R, lo haremos mediante la función polynomial(coef=...) e igualaremos el parámetro coef al vector de coeficientes en orden ascendente.

p = polynomial(coef = c(1,2,3,4,5))
p

1 + 2*x + 3*x^2 + 4*x^3 + 5*x^4

q = polynomial(coef = c(1,2,1))
q

1 + 2*x + x^2

Para comprobar si dos polinomios son iguales, utilizamos el operador lógico ==

p == q

[1] FALSE

Claramente son diferentes, porque, tal y como los hemos definido anteriormente, ni siquiera tienen el mismo grado

Una forma de calcular el grado de un polinomio en R es mediante la función length() aplicada al polinomio. Eso sí, teniendo en cuenta que, tal y como hemos definido los polinomios, $p(x)=a_0+\cdots+a_nx^n$, estos empiezan en 0. Con lo cual, para obtener el grado exacto del polinomio, habrá que restar una unidad al resultado que nos devuelva length():

gradoP = length(p)-1
gradoQ = length(q)-1
gradoP

[1] 4

gradoQ

[1] 2

Las operaciones suma y producto de polinomios, se llevan a cabo del siguiente modo:

#Suma
p+q

2 + 4*x + 4*x^2 + 4*x^3 + 5*x^4

#Producto de polinomios
p*q

1 + 4*x + 8*x^2 + 12*x^3 + 16*x^4 + 14*x^5 + 5*x^6

La divisióin de polinomios se realiza mediante /, pero con ello solo obtenemos el cociente. Para obtener el resto hay que utlizar %%:

cociente = p / q
resto = p%%q
cociente

10 - 6*x + 5*x^2

resto

-9 - 12*x

q*cociente + resto == p

[1] TRUE

Para evaluar polinomios, utilizaremos la función predict(polinomio,x0)

predict(p,1)

[1] 15

predict(q,0)

[1] 1

Para hallar las raíces de un polinomio, podemos utilizar la función polyroot introduciendo por parámetro el vector de coeficientes en orden creciente.

#Las raíces del polinomio x^2+2x+1
polyroot(c(1,2,1))

[1] -1-0i -1+0i

#Las raíces del polinomio x^2-4
polyroot(c(-4,0,1))

[1]  2+0i -2+0i

Fijaos que R nos devuelve un vector de números complejos a pesar de que las soluciones en ambos casos son dos números reales

0.3.2 Polinomios con `Python`

Para definir un polinomio en Python, lo haremos mediante las funciones sympy.symbols() para indicar con qué variable trabajamos y sympy.Poly() introduciendo el polinomio por parámetro:

import sympy 
x = sympy.symbols('x') 
p = sympy.Poly(x**2) 
p

Poly(x**2, x, domain='ZZ')

q = sympy.Poly(1+x+x**3) 
q

Poly(x**3 + x + 1, x, domain='ZZ')

O bien, otra forma de definir polinomios es mediante la librería numpy, introduciendo como parámetro el vector de coeficientes en orden descendente

import numpy
r = numpy.poly1d([1,2,1]) 
print(r)

   2
1 x + 2 x + 1

s = numpy.poly1d([1,2,3,4,5])
print(s)

   4     3     2
1 x + 2 x + 3 x + 4 x + 5

Para comprobar si dos polinomios son iguales, utilizamos el operador lógico ==

p == q

False

r == s

False

Claramente son diferentes, porque, tal y como los hemos definido anteriormente, ni siquiera tienen el mismo grado.

Observación. Fijaos que no podemos comparar los polinomios creados con librerías diferentes, ya que da error al ser diferentes tipos de objeto.

Para calcular el grado de cualquier polinomio en Python, lo haremos utilizando Polynomial.degree()

p.degree()

q.degree()

o, si estamos trabajando con la librería numpy, lo hacemos mediante la función Polynomial.order

r = numpy.poly1d([1,2,1]) 
s = numpy.poly1d([1,2,3,4,5])
r.order

s.order

¡Ojo! Fijaos que hemos tenido que volver a definir los polinomios. De no estar, la consola nos devolvería error.

Las operaciones suma y producto de polinomios, se llevan a cabo del siguiente modo:

p+q

Poly(x**3 + x**2 + x + 1, x, domain='ZZ')

p*q

Poly(x**5 + x**3 + x**2, x, domain='ZZ')

y, con la librería numpy, la suma y el producto de polinomios se realizan del siguiente modo:

r = numpy.poly1d([1,2,1]) 
s = numpy.poly1d([1,2,3,4,5])
r+s

poly1d([1, 2, 4, 6, 6])

r*s

poly1d([ 1,  4,  8, 12, 16, 14,  5])

La división de polinomios la obtenemos tal y como se muestra a continuación (solo utilizando la librería numpy):

r = numpy.poly1d([1,2,1]) 
s = numpy.poly1d([1,2,3,4,5])
s/r

(poly1d([1., 0., 2.]), poly1d([3.]))

r*numpy.poly1d([1,0,2])+3 == s

True

Observad que primero se devuelve el cociente y, a continuación, el resto de la división

Para evaluar polinomios, haciendo uso de la librería numpy, lo hacemos del siguiente modo:

r = numpy.poly1d([1,2,1]) 
s = numpy.poly1d([1,2,3,4,5])
r(0)

s(2)

Para encontrar las raíces de polinomios, haciendo uso de la librería numpy, lo hacemos utilizando Polynomial.r:

r = numpy.poly1d([1,2,1]) 
s = numpy.poly1d([1,2,3,4,5])
r.r

array([-1., -1.])

s.r

array([-1.28781548+0.85789676j, -1.28781548-0.85789676j,
        0.28781548+1.41609308j,  0.28781548-1.41609308j])

0.3.3 Polinomios con `Octave`

Para definir un polinomio en Octave, lo haremos mediante vectores. Para mostrarlos simbólicamente, utilizaremos la función polyout(vector,'variable'), donde las entradas del vector son los coeficientes en orden descendente.

p = [1,2,3,4,5]; 
polyout(p,'x') 
q = [1,0,0,1];
polyout(q,'x')

1*x^4 + 2*x^3 + 3*x^2 + 4*x^1 + 5
1*x^3 + 0*x^2 + 0*x^1 + 1

Una forma de calcular el grado de un polinomio en Octave es mediante la función length() aplicada al vector de coeficientes. Eso sí, teniendo en cuenta que, tal y como hemos definido los polinomios, $p(x)=a_0+\cdots+a_nx^n$, estos empiezan en 0. Con lo cual, para obtener el grado exacto del polinomio, habrá que restar una unidad al resultado que nos devuelva length():

p = [1,2,3,4,5]; 
q = [1,0,0,1];
gradoP = length(p)-1
gradoQ = length(q)-1

gradoP =  4
gradoQ =  3

Como, en Octave, los polinomios vienen representados por vectores, sumar polinomios no es una operación directa en Octave, ya que la mayoría de veces nos encontraremos con vectores de diferente longitud. En esos casos, se nos devolverá error por consola.

Lo mismo ocurre si quisiésemos comprobar que dos polinomios de diferente grado son iguales

Una solución a este problema es rellenar con 0 el vector de coeficientes hasta alcanzar la máxima longitud de los vectores que tengamos. Esto lo podemos conseguir mediante la función zeros():

p = [1,2,3,4,5]; q = [1,0,0,1]; gradoP = length(p)-1; gradoQ = length(q)-1;
p = [zeros(1, gradoQ-gradoP), p], q = [zeros(1, gradoP-gradoQ), q], suma = p+q

p =

   1   2   3   4   5

q =

   0   1   0   0   1

suma =

   1   3   3   4   6

Lo que sí podemos hacer es multiplicar polinomios mediante la función conv

p = [1,2,3,4,5];
q = [1,0,0,1];
producto = conv(p,q);
polyout(producto,'x')

1*x^7 + 2*x^6 + 3*x^5 + 5*x^4 + 7*x^3 + 3*x^2 + 4*x^1 + 5

La división de polinomios se consigue mediante la función deconv(numerador,denominador). Esta función devuelve los vecotres de coeficientes del cociente y el resto de la división polinómica, en orden descendente:

p = [1,2,3,4,5];
q = [1,0,0,1];
[cociente, resto] = deconv(p,q)

cociente =

   1   2

resto =

   0   0   3   3   3

Fijaos que el vector de coeficientes del resto tiene la misma longitud que el dividendo, con lo cual podemos realizar la comprobación de la división:

p = [1,2,3,4,5];
q = [1,0,0,1];
[cociente, resto] = deconv(p,q);
length(resto) == length(p)
p == conv(q,cociente) + resto

ans = 1
ans =

  1  1  1  1  1

donde los unos representan el valor lógico True

Para evaluar polinomios, utilizamos la función polyval(polinomio,x0):

p = [1,2,3,4,5];
q = [1,0,0,1];
polyval(p,0) 
polyval(q,3)

ans =  5
ans =  28

Para hallar las raíces de un polinomio, hacemos uso de la función roots():

p = [1,2,3,4,5];
q = [1,0,1];
roots(p)
roots(q)

ans =

   0.28782 + 1.41609i
   0.28782 - 1.41609i
  -1.28782 + 0.85790i
  -1.28782 - 0.85790i

ans =

  -0 + 1i
   0 - 1i

0.4 El principio de inducción

Principio de Inducción. El principio de inducción afirma que si $P(n)$ es una propiedad sobre $n\in\mathbb{N}$ y se cumple que

$P(1)$ es cierta (Caso base)
Si $P(n)$ es cierta, entonces $P(n+1)$ es cierta (Caso inductivo)

entonces $P(n)$ es cierta para todo $n\in\mathbb{N}$

El principio de Inducción también es válido si $n\in\mathbb{Z}$ del siguiente modo:

Si $P(n)$ es una propiedad sobre $n\in\mathbb{Z}$, con $n_0\in\mathbb{Z}$ y se cumple que

$P(n_0)$ es cierta
Si $P(n)$ es cierta, entonces $P(n+1)$ es cierta

entonces $P(n)$ es cierta para todo $n\in\mathbb{Z},\ n\ge n_0$

Principio de Inducción completa. Si $P(n)$ es una propiedad sobre $n\in\mathbb{N}$ y se cumple que

$P(1)$ es cierta (Caso base)
Si $P(n)$ es cierta para $1,2,\dots, n$, entonces $P(n+1)$ es cierta (Caso inductivo)

entonces $P(n)$ es cierta para todo $n\in\mathbb{N}$

El principio de Inducción completa también es válido si $n\in\mathbb{Z}$ del siguiente modo:

Si $P(n)$ es una propiedad sobre $n\in\mathbb{Z}$, $n_0\in\mathbb{Z}$ y se cumple que

$P(n_0)$ es cierta
Si $P(n)$ es cierta para $n_0\le n$, entonces $P(n+1)$ es cierta

entonces $P(n)$ es cierta para todo $n\in\mathbb{Z},\ n\ge n_0$

Curso Completo de Álgebra Lineal con R, Python y Octave

Preliminares

0.1 Cuerpos

0.1.1 La estructura de cuerpo

0.1.2 Propiedades de los cuerpos

0.1.3 Cuerpos conocidos

0.1.4 El cuerpo \(\mathbb{Z}_2\)

0.2 Números complejos

0.2.1 Plano Complejo

0.2.2 Forma polar

0.2.3 Números complejos con `R`

0.2.4 Trabajando con `Python` en Markdown

0.2.5 Números complejos con `Python`

0.2.6 Trabajando con `Octave` en Markdown

0.2.7 Números complejos con `Octave`

0.3 Polinomios

0.3.1 Polinomios con `R`

0.3.2 Polinomios con `Python`

0.3.3 Polinomios con `Octave`

0.4 El principio de inducción

Preliminares

0.1 Cuerpos

0.1.1 La estructura de cuerpo

0.1.2 Propiedades de los cuerpos

0.1.3 Cuerpos conocidos

0.1.4 El cuerpo \(\mathbb{Z}_2\)

0.2 Números complejos

0.2.1 Plano Complejo

0.2.2 Forma polar

0.2.3 Números complejos con R

0.2.4 Trabajando con Python en Markdown

0.2.5 Números complejos con Python

0.2.6 Trabajando con Octave en Markdown

0.2.7 Números complejos con Octave

0.3 Polinomios

0.3.1 Polinomios con R

0.3.2 Polinomios con Python

0.3.3 Polinomios con Octave

0.4 El principio de inducción

0.2.3 Números complejos con `R`

0.2.4 Trabajando con `Python` en Markdown

0.2.5 Números complejos con `Python`

0.2.6 Trabajando con `Octave` en Markdown

0.2.7 Números complejos con `Octave`

0.3.1 Polinomios con `R`

0.3.2 Polinomios con `Python`

0.3.3 Polinomios con `Octave`