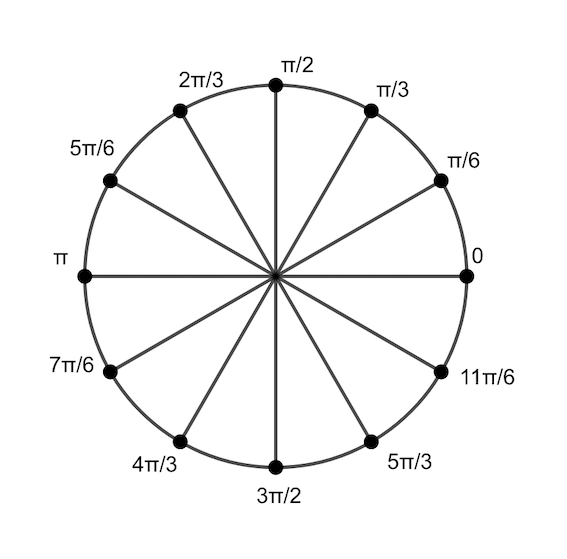
Apéndice de Trigonometría
Razones trigonométricas
\[\sin(x) = \frac{\text{cateto opuesto}}{\text{hipotenusa}}\]
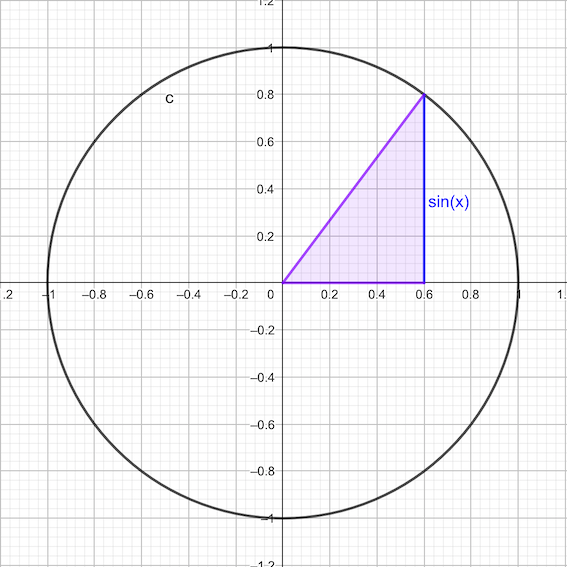
\[\cos(x) = \frac{\text{cateto contiguo}}{\text{hipotenusa}}\]
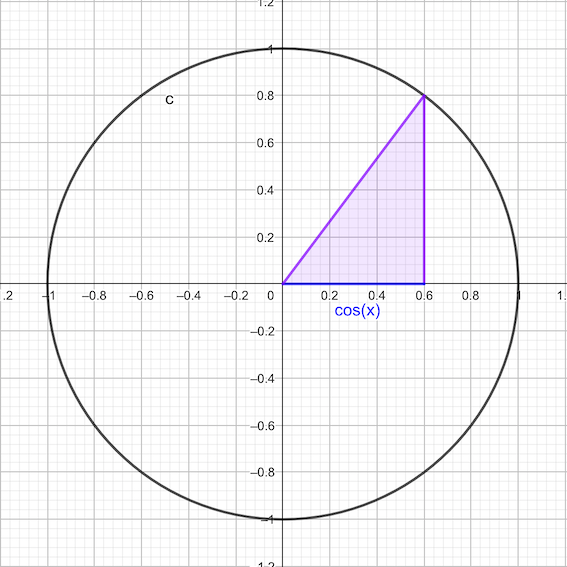
\[\tan(x) = \frac{\text{cateto opuesto}}{\text{cateto contiguo}} = \frac{\sin(x)}{\cos(x)}\]
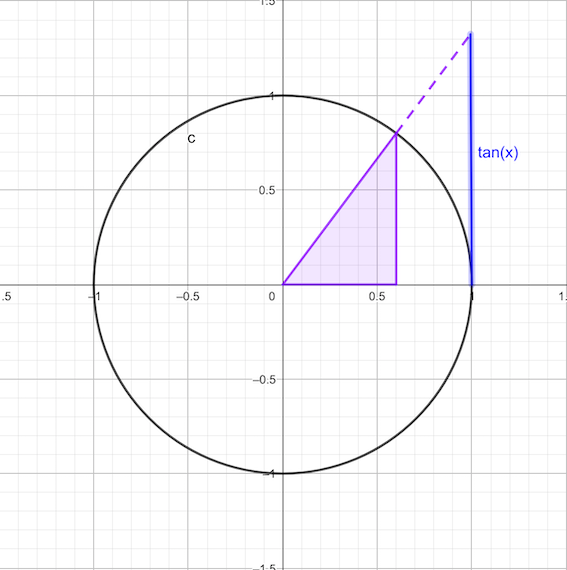
\[\csc(x) = \frac{1}{\sin(x)}\]
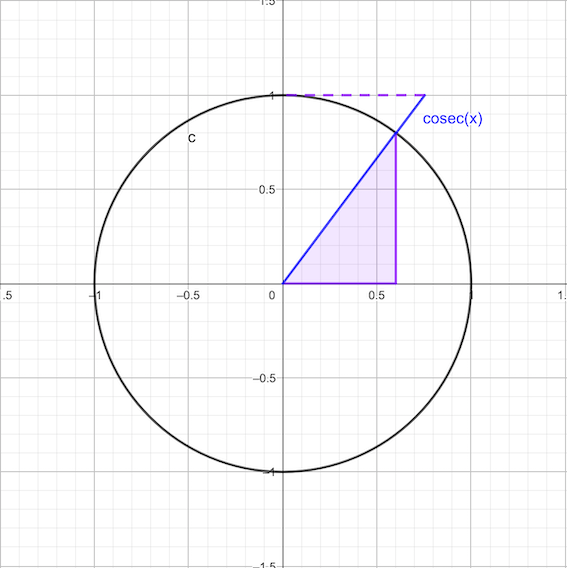
\[\sec(x) = \frac{1}{\cos(x)}\]
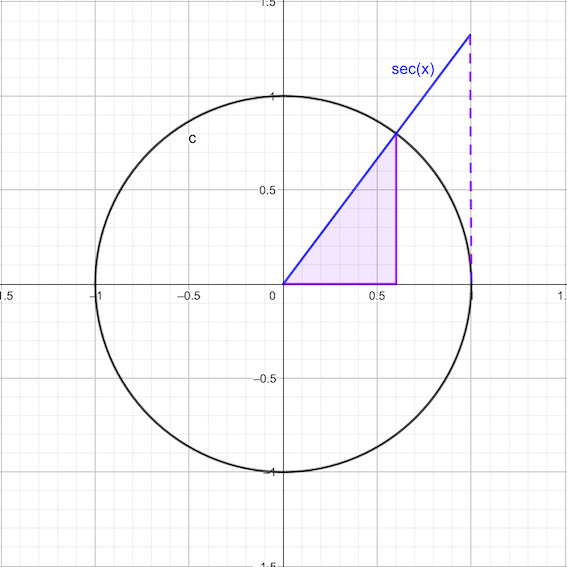
\[\cot(x) = \frac{1}{\tan(x)}\]
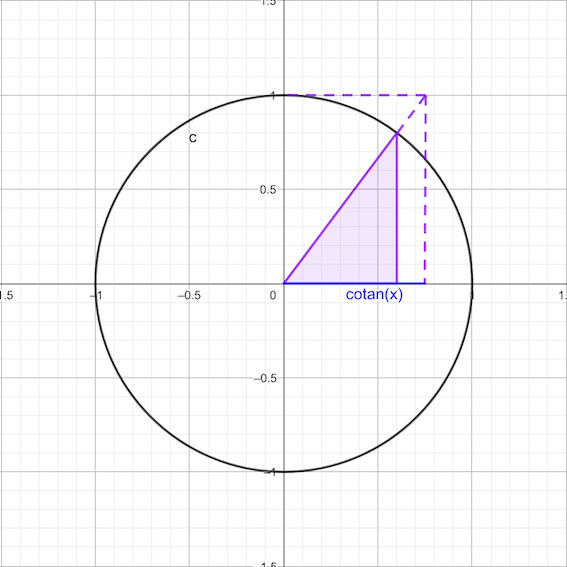
Relaciones trigonométricas
Relaciones fundamentales
\[\sin^2(\alpha)+\cos^2(\alpha) = 1\] \[1+\tan^2(\alpha)= \frac{1}{\cos^2(\alpha)}\]
Relaciones pitagóricas
\[1+\cot^2(\alpha) = \csc^2(\alpha)\] \[1+\tan^2(\alpha) = \sec^2(\alpha)\]
Relaciones entre las razones trigonométricas
Ángulos opuestos
\[\begin{matrix} \sin(-\alpha) = -\sin(\alpha) && \cos(-\alpha) = \cos(\alpha)&&\tan(-\alpha) = -\tan(\alpha)\\ \sin(2\pi-\alpha) = -\sin(\alpha) &&\cos(2\pi-\alpha) = \cos(\alpha) && \tan(2\pi-\alpha) = -\tan(\alpha) \end{matrix}\]
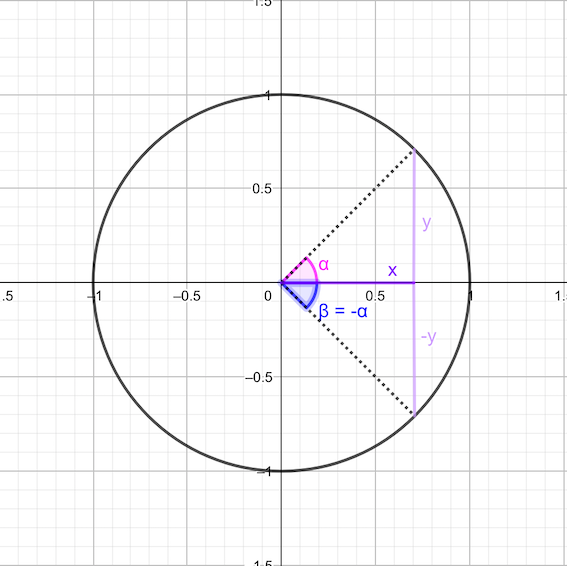
Ángulos suplementarios
\[\sin(\pi\pm \alpha) = \mp\sin(\alpha)\] \[\cos(\pi\pm \alpha) = -\cos(\alpha)\] \[\tan(\pi\pm \alpha) = \mp\tan(\alpha)\]
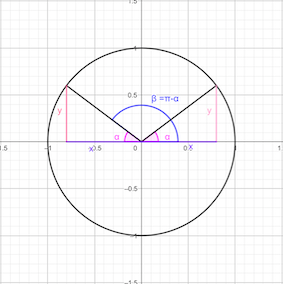
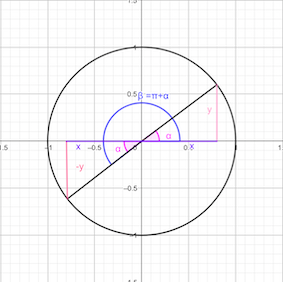
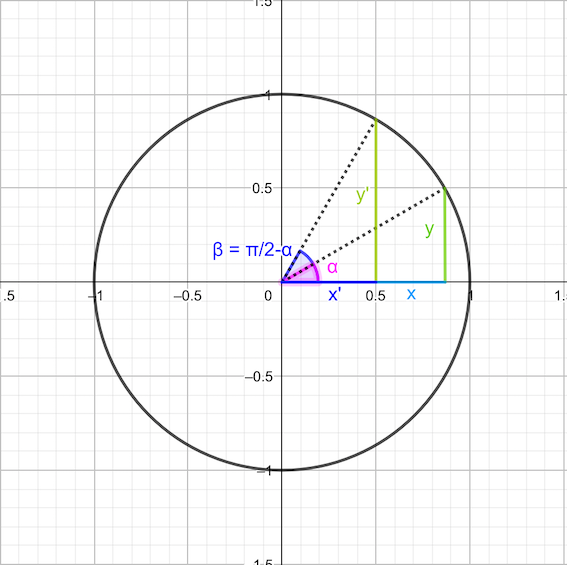
Ángulos complementarios
\[\sin\left(\frac{\pi}{2}\pm \alpha\right) = \cos(\alpha)\] \[\cos\left(\frac{\pi}{2}\pm \alpha\right) = \mp\sin(\alpha)\] \[\tan\left(\frac{\pi}{2}\pm \alpha\right) = \mp\frac{1}{\tan(\alpha)}\]
Suma o resta de ángulos
\[\sin(\alpha\pm \beta) = \sin(\alpha)\cos(\beta)\pm \cos(\alpha)\sin(\beta)\] \[\cos(\alpha\pm \beta) = \cos(\alpha)\cos(\beta)\mp \sin(\alpha)\sin(\beta)\]
\[\tan(\alpha\pm \beta) = \frac{\tan(\alpha)\pm\tan(\beta)}{1\mp\tan(\alpha)\tan(\beta)}\]
Ángulo doble
\[\sin(2\alpha) = 2\sin(\alpha)\cos(\alpha)\] \[\cos(2\alpha) = \cos^2(\alpha)-\sin^2(\alpha)\]
\[\tan(2\alpha) = \frac{2\tan(\alpha)}{1-\tan^2(\alpha)}\]
Ángulo mitad
\[\sin\left(\frac{\alpha}{2}\right) =\pm\sqrt{\frac{1-\cos(\alpha)}{2}} \] \[\cos\left(\frac{\alpha}{2}\right) =\pm\sqrt{\frac{1+\cos(\alpha)}{2}} \]
\[\tan\left(\frac{\alpha}{2}\right) =\pm\sqrt{\frac{1-\cos(\alpha)}{1+\cos(\alpha)}} \]
Sumas y Restas de senos y cosenos
\[\begin{matrix} \sin(\alpha)+\sin(\beta) = 2\sin\left(\frac{\alpha+\beta}{2}\right)\cos\left(\frac{\alpha-\beta}{2}\right)&&\sin(\alpha)-\sin(\beta) = 2\cos\left(\frac{\alpha+\beta}{2}\right)\sin\left(\frac{\alpha-\beta}{2}\right)\\ \cos(\alpha)+\cos(\beta) = 2\cos\left(\frac{\alpha+\beta}{2}\right)\cos\left(\frac{\alpha-\beta}{2}\right)&&\cos(\alpha)-\cos(\beta) = -2\sin\left(\frac{\alpha+\beta}{2}\right)\sin\left(\frac{\alpha-\beta}{2}\right) \end{matrix}\]
Valores del seno, coseno y tangente usuales
| Radianes | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) |
|---|---|---|---|---|---|
| Grados | \(0º\) | \(30º\) | \(45º\) | \(60º\) | \(90º\) |
| sin | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) |
| cos | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(0\) |
| tan | \(0\) | \(\frac{\sqrt{3}}{3}\) | \(1\) | \(\frac{3}{\sqrt{3}}\) | \(\infty\) |
Otros resultados de trigonometría
Proyección del segmento \(\bar{AB}\) sobre una recta \(r\)
\[\bar{A'B'} = \bar{AB}\cos(\alpha)\]
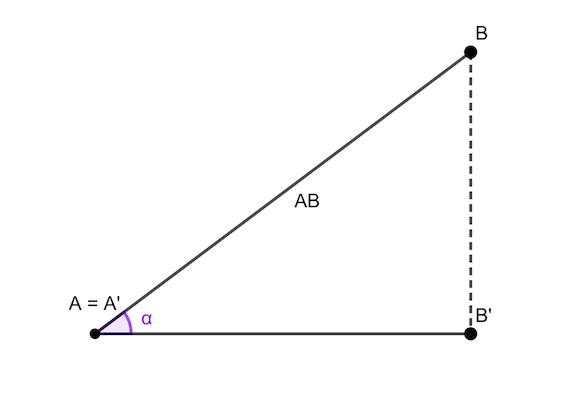
Área de un triángulo
\[A = \frac{1}{2}ab\sin(\alpha) = \frac{bh}{2}\]
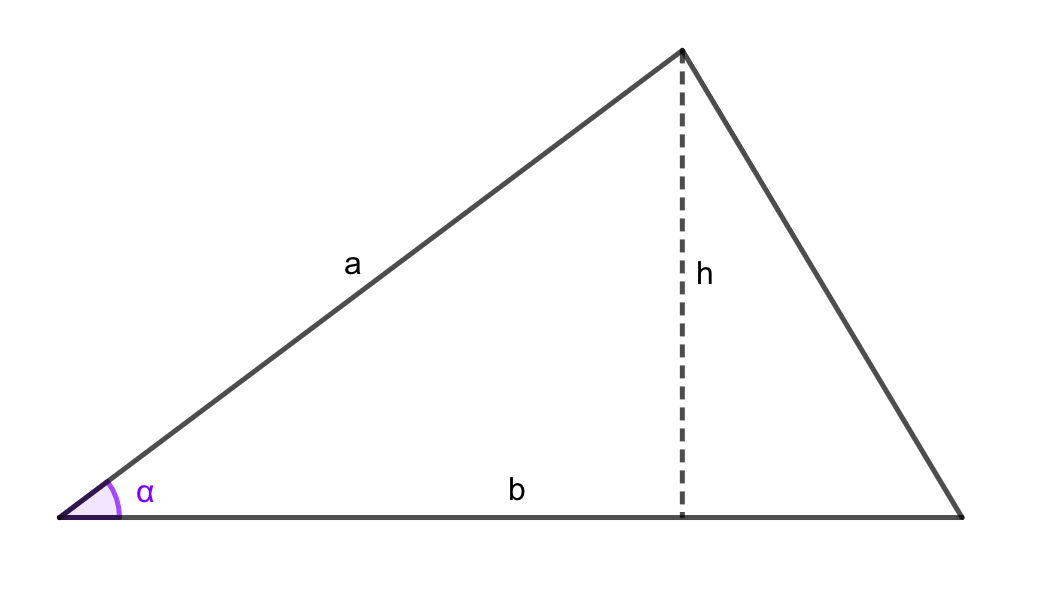
Teorema de los senos
\[\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)}\]
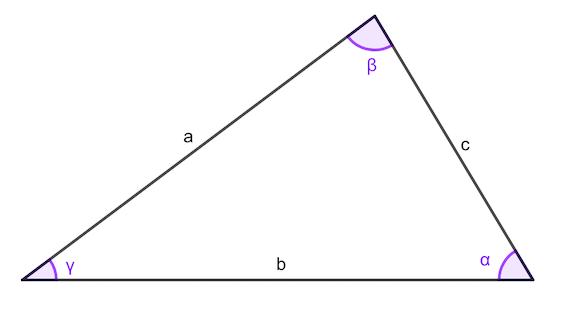
Teorema del coseno
\[a^2 = b^2+c^2-2bc\cos(\alpha)\] \[b^2 = a^2+c^2-abc\cos(\beta)\] \[c^2 = a^2+b^2-2ab\cos(\gamma)\]

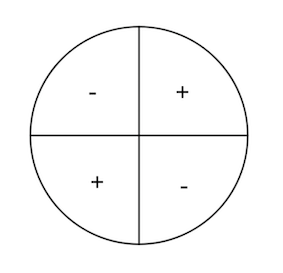
Más sobre seno, coseno y tangente
| Seno | Coseno | Tangente |
|---|---|---|
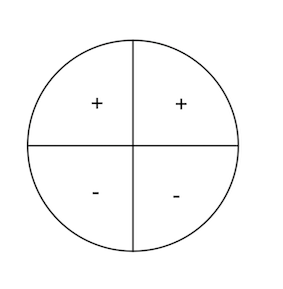 |
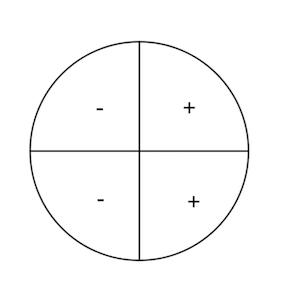 |
 |