Parte 6 Aprendizaje por Refuerzo

6.1 Upper Confidence Bound (UCB)

6.1.1 Intuición de UCB

Exercise 6.1

¿Podrías explicar con más detalle qué es una distribución? ¿Qué hay en el eje \(x\) y en el eje \(y\)?

Supongamos que tenemos un experimento con hacer clic en un anuncio 100 veces y calculamos cuál es la frecuencia con la que se hace clic en el anuncio. Luego lo repetimos nuevamente por otras 100 veces. Y nuevamente por otras 100 veces. De ahí obtenemos muchas frecuencias. Si repetimos estos cálculos de frecuencia muchas veces, por ejemplo 500 veces, podemos trazar un histograma de estas frecuencias. Según el Teorema central del límite, tendremos una forma de campana y su media será la media de todas las frecuencias que obtuvimos durante el experimento. Por lo tanto, en conclusión, en el eje \(x\) tenemos los diferentes valores posibles de estas frecuencias, y en el eje \(y\) tenemos el número de veces que obtuvimos cada frecuencia durante el experimento.

Exercise 6.2

En la primera conferencia sobre intuición, ¿podrías explicar por qué D5 (en naranja) es la mejor distribución? ¿Por qué no es D3 (en rosa)?

En esta situación, 0 es pérdida y 1 es ganancia o victoria. El D5 es el mejor porque está sesgado a la derecha, por lo que tendremos resultados promedio cercanos a 1, lo que significa que tenemos más victorias o ganancias. Y, de hecho, todas las máquinas de casino de hoy en día están cuidadosamente programadas para tener una distribución como D1 o D3. Pero es un buen ejemplo concreto.

6.1.2 UCB en Python

Exercise 6.3

¿Por qué una sola ronda puede tener varios 1 para diferentes anuncios?

Cada ronda corresponde a un usuario que se conecta a una página web, y el usuario solo puede ver un anuncio cuando se conecta a la página web, el anuncio que se le está mostrando. Si hace clic en el anuncio, la recompensa es 1; de lo contrario, 0. Y puede haber varios porque hay varios anuncios en los que al usuario le encantaría hacer clic. Pero solo una bola de cristal nos diría en qué anuncios haría clic el usuario. Y el conjunto de datos es exactamente esa bola de cristal (aquí estamos haciendo una simulación).

Exercise 6.4

¿Podrías explicar con más detalle qué hacemos con las recompensas en las líneas de código 33y 34?

Vamos a verlo en detalle:

• En la línea 33, solo obtenemos la recompensa en la ronda \(n\) específica. Entonces obtenemos un 1 si el usuario hace clic en el anuncio en esta ronda \(n\), y un 0 si el usuario no lo hace.
• En la línea 34 obtenemos la suma de todas las recompensas hasta la ronda \(n\). Entonces, esta suma se incrementa en 1 si el usuario hace clic en el anuncio en esta ronda \(n\), y permanece igual si el usuario no lo hace.

Exercise 6.5

¿Entra realmente en vigor la estrategia UCB durante las primeras rondas?

No al principio, primero debemos tener algunos primeros conocimientos de la respuesta de los usuarios a los anuncios. Ese es solo el comienzo de la estrategia.

En el mundo real, para los primeros diez usuarios que se conectan a la página web, se mostraría el anuncio 1 al primer usuario, el anuncio 2 al segundo usuario, el anuncio 3 al tercer usuario,…, el anuncio 10 al décimo usuario. Entonces comenzaría a actuar el algoritmo.

Exercise 6.6

¿Cuál fue el propósito de este algoritmo? ¿Por qué no podía simplemente contar qué tipo de anuncio convierte más y luego usarlo?

Porque en cada ronda hay un coste (el coste de poner un anuncio en la página). Entonces, básicamente, el propósito de UCB no es solo maximizar los ingresos, sino también minimizar el coste. Y si solo se cuenta qué tipo de anuncio convierte mejor, eso requeriría que se experimentara durante muchas rondas y, por lo tanto, el costo sería más alto y definitivamente no se minimizaría…

6.1.3 UCB en R

Exercise 6.7

¿Cómo obtener este tipo de conjunto de datos?

En la vida real, podríamos hacer esto mediante la transmisión de datos, utilizando Spark o Hive, lo que significa que obtendríamos datos en tiempo real. De lo contrario, si deseas evaluar tus modelos de aprendizaje por refuerzo, puedes simular un conjunto de datos como el que usamos en las clases.

Exercise 6.8

¿Cuál es exactamente el ‘number of selections’?

“number of selections” es el número de veces que se muestra el anuncio a un usuario.

Exercise 6.9

No entiendo por qué el algoritmo no selecciona anuncios en las primeras 10 rondas. El instructor dice que no hay una estrategia al principio, por lo que la primera ronda mostrará el anuncio 1, el anuncio 2 de la segunda ronda, el anuncio 3 de la tercera ronda, etc.

Porque en este punto no sabemos nada sobre los anuncios y no podemos aplicar nuestra fórmula porque implica la división por cuántas veces se ha mostrado un anuncio. No podemos dividir por 0…

Exercise 6.10

En Python, el anuncio ganador fue el anuncio no. 4 y en R fue el anuncio no. 5. Sin embargo, se ha utilizó el mismo archivo Ads_CTR_Optimisation.csv. ¿Por qué estamos obteniendo dos resultados diferentes usando la misma lógica?

Porque los índices en Python comienzan desde 0 y los índices en R comienzan desde 1. Por lo tanto, Python y R se obtienen el mismo anuncio.

Exercise 6.11

¿Podrías mostrar una implementación en R de la curva de arrepentimiento del UCB?

# Importando el conjunto de datos
dataset = read.csv('Ads_CTR_Optimisation.csv')

# Implementar UCB
N = 10000
d = 10
ads_selected = integer(0)
numbers_of_selections = integer(d)
sums_of_rewards = integer(d)
total_reward = 0
rewards_at_each_step=integer(0)
best_selection=(rowSums(dataset)==0) # Línea nueva
best_rewards_at_each_step=integer(0) # Línea nueva
for (n in 1:N) {
  ad = 0
  max_upper_bound = 0
  for (i in 1:d) {
    if (numbers_of_selections[i] > 0) {
      average_reward = sums_of_rewards[i] / numbers_of_selections[i]
      delta_i = sqrt(3/2 * log(n) / numbers_of_selections[i])
      upper_bound = average_reward + delta_i
    } else {
        upper_bound = 1e400
    }
    if (upper_bound > max_upper_bound) {
      max_upper_bound = upper_bound
      ad = i
    }
  }
  ads_selected = append(ads_selected, ad)
  numbers_of_selections[ad] = numbers_of_selections[ad] + 1
  reward = dataset[n, ad]
  sums_of_rewards[ad] = sums_of_rewards[ad] + reward
  total_reward = total_reward + reward
  rewards_at_each_step=c(rewards_at_each_step, total_reward) # Línea nueva
  best_rewards_at_each_step[n]=sum(best_selection[1:n]) # Línea nueva
}

# Curva de Arrepentimiento
plot(best_rewards_at_each_step, pch='.', col=3, 
    main="Real and Imaginary Rewards; Regret",
    ylab="Reward Numbers")
points(rewards_at_each_step, pch=".", col=4)
points((best_rewards_at_each_step-rewards_at_each_step), 
       pch='.', col="darkgoldenrod")
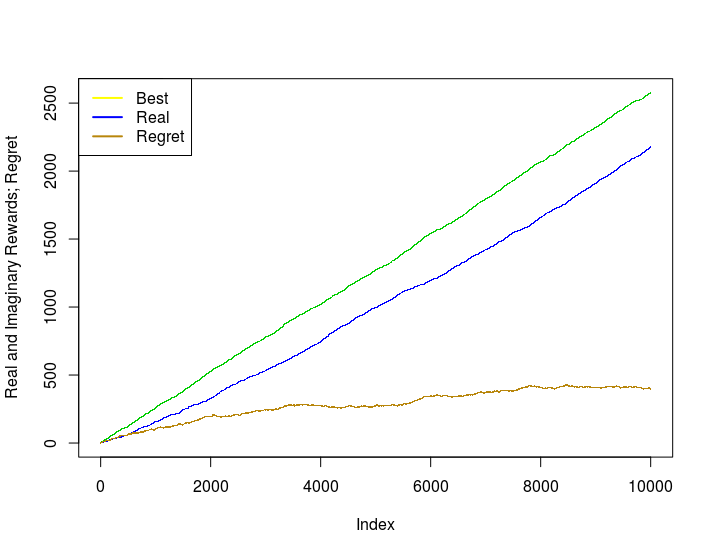
legend('topleft', legend=c("Best", "Real", "Regret"), 
    col=c(7,4, "darkgoldenrod"),  horiz=F, lty=1, lwd=2)

Y obtenemos las siguientes curvas:

6.2 Muestreo Thompson

6.2.1 Intuición del Muestreo Thompson

Exercise 6.12

¿Por qué la marca amarilla es la mejor opción y no la marca verde?

La marca amarilla es la mejor opción porque es la más alejada del origen en el eje x, lo que significa que tiene el retorno estimado más alto.

Exercise 6.13

¿Por qué es el muestreo Thompson mejor que UCB?

El muestreo Thompson es mejor que UCB en términos de convergencia de la curva de arrepentimiento. El arrepentimiento es la diferencia entre la recompensa óptima y la recompensa que acumula con nuestro algoritmo. El muestreo Thompson muestra una mejor curva de arrepentimiento que UCB en mi experiencia. Además, el hecho de que UCB sea determinista en lugar de que el muestreo Thompson sea estocástico, ayuda a que el muestreo Thompson supere a UCB. Además en las secciones prácticas se ve que el muestro Thompson es capaz de encontrar el mejor anuncio más rápido y con más certeza que UCB.

Exercise 6.14

No entiendo cómo Thompson Sampling puede aceptar comentarios retrasados.

Al hacer el muestreo de Thompson, aún podemos realizar actualizaciones en nuestro algoritmo (como hacer nuevas conjeturas para las distribuciones con datos existentes, muestrear de la distribución adivinada, etc.) mientras esperamos los resultados de un experimento en el mundo real. Esto no obstaculizaría el funcionamiento de nuestro algoritmo. Es por eso que puede aceptar retroalimentación retrasada.

Exercise 6.15

¿Cuáles son otros ejemplos de aplicaciones de muestreo de Thompson?

Otra aplicación potencial del problema delbandido multibrazo puede ser la prueba en línea de algoritmos.

Por ejemplo, supongamos que tenemos un sitio web de comercio electrónico y tiene a su disposición varios algoritmos de aprendizaje automático para proporcionar recomendaciones a los usuarios (de lo que sea que venda el sitio web), pero no sabemos qué algoritmo conduce a las mejores recomendaciones…

Podemos considerar el problema como un problema de UCB y definir cada algoritmo de aprendizaje automático como un “brazo”: en cada ronda, cuando un usuario solicita una recomendación, se seleccionará un brazo (es decir, uno de los algoritmos) para hacer las recomendaciones y recibiremos la recompensa. En este caso, podemos definir la recompensa de varias formas, un ejemplo simple es “1” si el usuario hace clic / compra un artículo y “0” en caso contrario. Eventualmente, el algoritmo del bandido multibrazo bandidos convergerá y terminará eligiendo siempre el algoritmo que sea más eficiente para brindar recomendaciones. Ésta es una buena forma de encontrar el modelo más adecuado en un problema en línea.

Otro ejemplo que me viene a la mente es encontrar el mejor tratamiento clínico para los pacientes: cada tratamiento posible podría considerarse como un “brazo”, y una forma sencilla de definir la recompensa sería un número entre 0 (el tratamiento no tiene ningún efecto) y 1 (el paciente se cura perfectamente).

En este caso, el objetivo es encontrar lo más rápido posible el mejor tratamiento minimizando el arrepentimiento acumulativo (lo que equivale a decir que desea evitar en la medida de lo posible la selección de tratamientos “malos” o incluso subóptimos durante el proceso).

6.2.2 Muestreo Thompson en Python

Exercise 6.16

¿Dónde puedo encontrar un gran recurso sobre la distribución Beta?

El mejor link es el siguiente: Distribución Beta

Exercise 6.17

El histograma muestra 4 como el mejor anuncio para seleccionar. La barra más alta está en 4 en el eje x. ¿Por qué se indica como 5?

Es solo porque los índices en Python comienzan desde 0. Entonces, el anuncio del índice 4 es el anuncio número 5.

Exercise 6.18

Tengo curiosidad por saber cómo se aplicaría el muestreo de Thompson de forma proactiva al ejecutar esta campaña publicitaria teórica. ¿Repetiríamos el programa en cada ronda (es decir, cada vez se presentaran todas los anuncios al usuario)?

Primero, un ingeniero de datos crea una canalización para leer los datos del sitio web y reaccionar a ellos en tiempo real. Luego, una visita a la web genera una respuesta para volver a calcular nuestros parámetros y elegir un anuncio para la próxima vez que alguien se conecte.

6.2.3 Muestreo Thompson en R

Exercise 6.19

¿Podrías explicar la diferencia entre las distribuciones Bernoulli y Beta?

La distribución de Bernoulli se aplica a probabilidades discretas porque proporciona la probabilidad de éxito de un resultado, mientras que la distribución Beta se aplica a funciones de densidad (continuas), utilizando una función de deensidad. Esa es la principal diferencia. Aquí hay algunos recursos excelentes:

• Distribución de Bernoulli
• Distribución Beta

Exercise 6.20

¿Podrías proporcionar alguna explicación sobre la inferencia bayesiana?

Este es bastante bueno: Inferencia Bayesiana

Exercise 6.21

¿Cómo puede la heurística del muestreo Thomson encontrar rápidamente que el quinto anuncio es el mejor en comparación con la heurística de Upper Confidence Bound?

Es difícil explicar la razón teóricamente, eso requeriría hacer una investigación y escribir una demostración matemática extensa. Pero intuitivamente, podría deberse a que UCB se basa en suposiciones optimistas, mientras que el muestreo de Thompson se basa en probabilidades relevantes a través del enfoque bayesiano.

Exercise 6.22

¿Cómo representar la curva de arrepentimiento de muestreo de Thompson en R?

Básicamente, simplemente necesitas agregar lo siguiente al final de nuestro código:

rewards_at_each_step=c(rewards_at_each_step, total_reward)
  best_rewards_at_each_step[n]=sum(best_selection[1:n])
}
plot(best_rewards_at_each_step, pch='.', col=3, 
     main="Real and Imaginary Rewards; Regret",
     ylab="Reward Numbers")
points(rewards_at_each_step, pch=".", col=4)
points((best_rewards_at_each_step-rewards_at_each_step), 
       pch='.', col="darkgoldenrod")
legend('topleft', legend=c("Best", "Real", "Regret"), 
       col=c(7,4, "darkgoldenrod"),  horiz=F, lty=1, lwd=2)